一种基于FPGA的二维相控阵天线配相算法实现方法

江承财 李 明 张小虎 云 龙

(1.西安电子工程研究所 西安 710100；2.陆军装备部驻西安地区军事代表局 西安 710032)

0 引言

60年代发展起来的二维平面相控阵，主要应用在外太空目标监视和战略预警等重要场合。随着相控阵总体技术发展和核心移相组件制造工艺日趋成熟、成本不断降低，二维平面相控阵日益广泛地应用在战术雷达领域。相控阵雷达TAS、TWS、分区搜索、Burnt Out等多种功能主要得益于天线波束快速扫描和快速赋形的技术特点。相较于一维相控阵，二维平面相控阵雷达工作模式更加多样化，对波束捷变要求更高，同时因其移相单元数量巨大，系统对波束控制电路响应速度提出了更高的要求。

常见的波束控制电路硬件架构一般基于DSP、专用ASIC芯片或FPGA芯片。DSP硬件架构波束控制电路在一维线阵相控阵雷达中应用较多，其控制规模较小，配相计算响应时间控制在雷达系统时序可接受范围，其优势在于电路调试效率较高,实现速度快；专用ASIC波束控制芯片较多见于批产相控阵天线或子阵波束控制中，其设计成本较高，但在定型批产应用后效益明显；FPGA芯片架构的波束控制电路，其成本适中，适合于小批量生产过程和批产先期验证，其丰富的存储器资源、DSP资源、IO资源以及硬件并行运算特性，有利于快速实现配相算法和配相控制信息传输，满足天线波束高速扫描需求。

本文首先解析二维相控阵配相计算方程，获得适用于FPGA架构的配相算法；然后利用FPGA芯片丰富的存储器资源、DSP资源和并行运算特性实现架构优化的配相算法；最后通过误差分析比对，验证了基于FPGA的二维相控阵天线配相算法的运算精度。

1 二维平面相控阵配相方程解析

以矩形格均匀阵排列天线单元的二维平面阵列进行配相方程解析。图1为天线单元分布和坐标关系图。天线阵面在xoy平面上，共M×N个移相单元，单元间距分别为dx和dy，dx为x轴方向单元间距，dy为y轴方向单元间距，z轴为天线法线方向。

以球坐标表示目标方向矢量，其中方位角φ定义为目标方向矢量在xz平面投影线与z轴夹角，俯仰角θ定义为目标方向矢量与其在xz平面投影线夹角。目标方向以方向余弦表示为(cosαx，cosαy，cosαz)[1]，天线单元到目标方向之间存在的路程差决定了信号传输过程中的相位差。相邻单元之间的空间相位差，沿x轴和y轴方向分别为

(1)

(2)

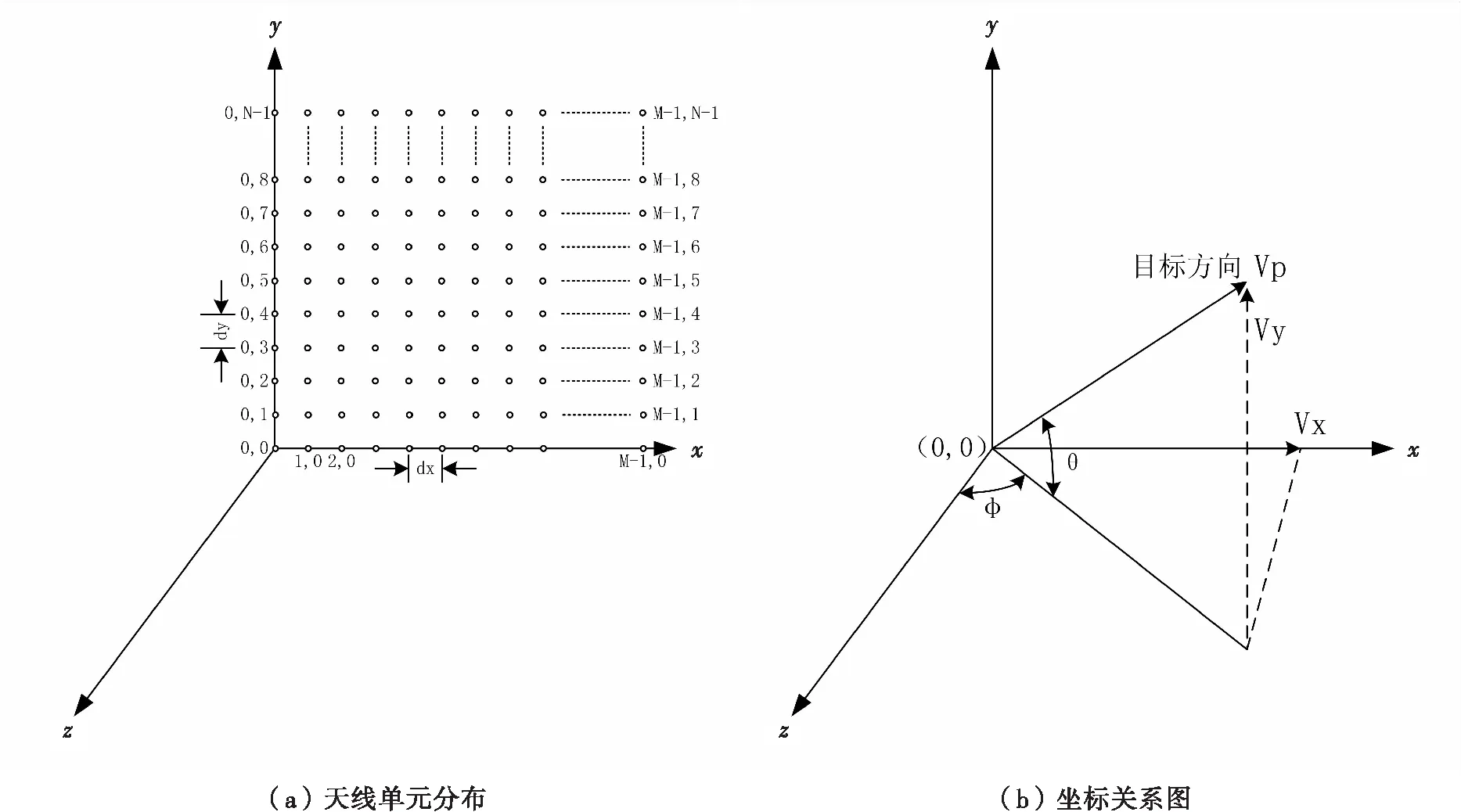
图1 天线单元分布和坐标关系图

第(i，k)单元与第(0,0)单元之间的空间相位差为

ΔΦik=iΔφx+kΔφy

(3)

设天线移相单元提供的阵内相位差为

ΔΦBik=iΔφBx+kΔφBy

(4)

则图1所示二维平面阵列方向图为

(5)

在图1定义的球坐标系中，有

(6)

将式(6)代入式(5)，方向图又可表示为

(7)

由式(7)可知，当阵内相位差满足

(8)

条件时，将在(θ，φ)方向获得方向图最大值，即实现天线波束在该方向上的指向。将式(8)代入式(4)，可得此时天线单元(i，k)的阵内相位差为

(9)

式(9)即为均匀分布二维平面阵列的配相方程，按该式计算M×N个天线单元阵内相位差，并将相应移相单元相位置为计算获得的相位值即可将天线波束指向(θ，φ)方向。

2 二维平面相控阵配相算法的FPGA实现

在非超宽带系统中，若不考虑延迟线应用，各天线单元计算获取的相移值以2π为周期取模。在实际天线系统中的移相单元一般采用数字式移相器，其移相步进受限于移相器基本位位数，相位控制码需按移相步进量化。因此针对式(9)的配相方程，配相计算过程还包括以下两个步骤。

(10)

(11)

式(11)为基于数字移相器的二维平面相控阵配相方程。其中，i为方位向天线单元计数，k为俯仰向天线单元计数，dx为方位向天线单元间距，dy为俯仰向天线单元间距，θ为俯仰角，φ为方位角，λ为辐射微波信号波长，n为数字移相器位数。有λ=c/f，同时将弧度表示为角度，式(11)可化为

(12)

式(12)中c为光速，工程应用中一般取299792458 m/s。由于数字移相器移相表现为滞后相移，因此取配相码时有

(13)

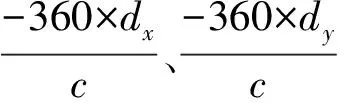
在FPGA内部进行配相计算，为提高运算速度，有必要将浮点运算变换为定点运算，并尽量简化运算过程[2]。根据FPGA运算特性，将式(13)进一步改造为

Ph_Code=Round{mod[(imxf/s×2pcosθ×2qsinφ×
2w+kmyf/s×2rsinθ×2t+φ(i,k)/s×2u),2n+u]}≫u

(14)

式(14)中，s=360/2n，为数字移相器相移步进量，其值为常量；2p、2q、2w、2r、2t皆为配相计算参数浮点化定点的放大倍数；φ(i,k)为天线单元(i，k)的通道初始相位。

FPGA内部的Block RAM存储器资源，支持实现单口ROM、双口ROM等多种静态存储器[3]。将式(14)中部分乘法、除法、余弦函数、正弦函数、浮点转定点等过程先期进行预运算，计算结果作为FPGA静态存储器的初始化文件，建立相应查找ROM。配相计算过程中以查表方式代替这些实现复杂、耗时较多的环节，减轻计算时序压力。以频率点为索引变量，建立方位向、俯仰向频率信息查找表，表内存储内容分别为Round(mxf/s×2p)、Round(myf/s×2r)，数据类型为有符号整数；以俯仰角波位号为索引变量，建立俯仰角余弦查找表、正弦查找表，表内存储内容分别为Round(cosθ×2q)、Round(sinθ×2t)，数据类型为有符号整数；以方位角波位号为索引变量，建立方位角正弦查找表，表内存储内容为Round(sinφ×2w)，数据类型为有符号整数；以频率点和天线单元在方位、俯仰向的单元计数i、k为索引，建立初始相移查找表，表内存储内容为Round(φ(i,k)/s×2u)。

式(14)求和的三组参量imxf/s×2pcosθ×2qsinφ×2w、kmyf/s×2rsinθ×2t和φ(i,k)/s×2u已经进行移相步进量化，且放大倍数皆为u，故将其求和后按2n+u取模右移u位即获得配相码值。

图2为配相算法在FPGA平台实现的基本流程图。为进一步改善计算精度，减小量化误差带来的影响，将配相计算过程中产生的量化残差迭代进入计算流程[4]。

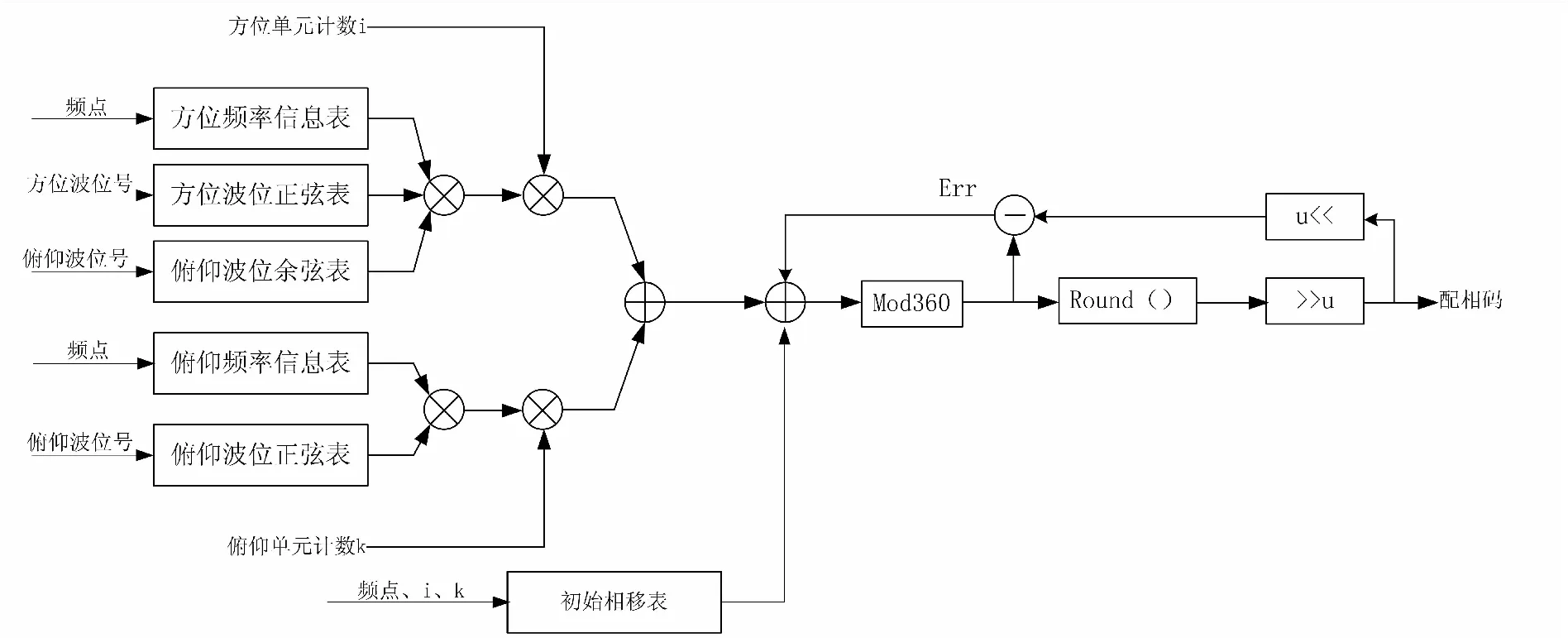
图2 FPGA平台实现二维配相算法基本流程图

利用FPGA丰富的DSP资源，可以并行开展多单元配相计算。M×N规模的天线阵列，若DSP资源充足，可以按行N或列M展开配相计算，整阵计算耗时等同于单行或单列线阵的配相计算时间，为顺序执行指令方式配相计算的1/N或1/M。在某24×48规模的二维平面相控阵配相过程中，按行展开配相计算，并列进行24组配相计算支路，每支路计算48个天线单元配相码，设计计算节拍脉冲为10 MHz，计算完成全阵所有天线单元配相码仅耗时4.8 μs，与顺序执行计算方式相比，耗时量极大程度减小。为进一步缩减波束控制响应时间，可以在配相计算和配相控制信息传输之间安排流水作业，将大部分配相计算时间覆盖在有源组件结构形式和传输速率决定的配相控制信息传输时间内，理论上可以将独立配相计算时间开销压缩至2～3个计算节拍。图3为M×N规模的天线阵列按行展开并行配相计算流程图。

3 算法误差分析

二维平面相控阵配相算法在FPGA平台上实现，其主要过程包括数据量化、数据转换、查表、并行运算等步骤。算法的精度与数据量化转换带来的误差直接相关，当放大倍数因子2u越大，则四舍五入误差噪声越小，对算法的精度影响越小[5]。为平衡FPGA资源利用率、运算速度、运算精度和FPGA系统功耗，需合理设置放大倍数因子2u。放大倍数因子2u确定后，根据天线阵指向角精度要求、频率点数等实际情况动态调整式(14)中2p、2q、2w、2r、2t参数。经仿真计算，证明配相算法精度与放大倍数因子2u直接相关。图4为某24×48规模二维平面相控阵第(3,5)单元基于FPGA的配相码计算结果与Matlab使用双精度浮点配相计算结果误差统计。统计在0.01°波束跃度随机指向情况下，200次配相码计算过程中不同放大倍数因子对FPGA配相码计算误差造成的影响。

在某24×48规模的二维平面相控阵配相过程中，当放大倍数因子达到248以上时，通过合理调整2p、2q、2w、2r、2t参数，FPGA计算结果与Matlab双精度浮点运算结果完全一致。

4 结束语

本文基于FPGA的二维相控阵天线配相算法，充分利用了FPGA芯片架构优势，依赖其丰富的存储器资源、DSP资源和并行运算特性，可以实现大规模二维相控阵天线高速高精度配相计算，满足天线波束高速扫描需求。另外，相较于其他硬件架构的配相方式，应用该算法实现二维相控阵天线波束控制，波控系统集成度、可靠性、软件可移植性均有较大改善。

图3 M×N阵列按行展开配相算法流程图

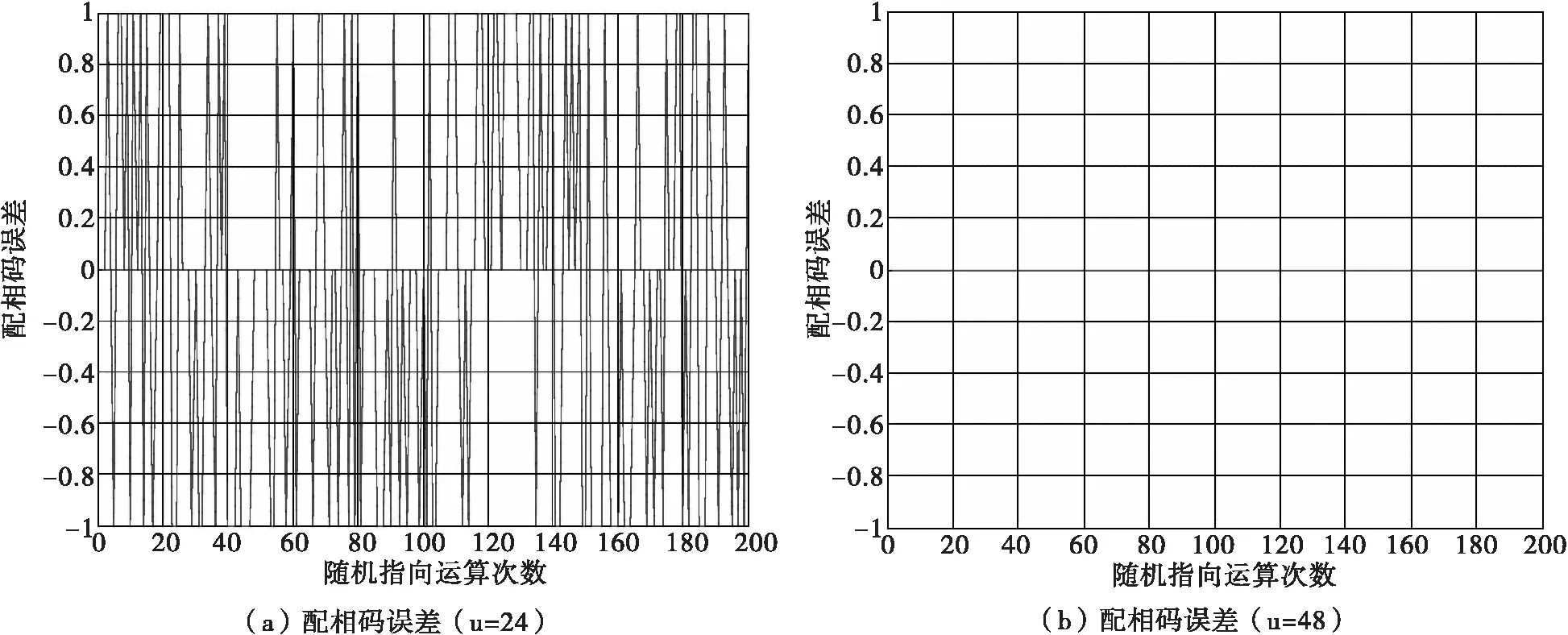
图4 配相码误差统计