一种复合制导的地空导弹武器系统中末制导交接班概率仿真分析

2020-05-08陈绪龙郝士林

火控雷达技术 2020年1期

严超陈绪龙郝士林

(西安电子工程研究所西安 710100)

0 引言

随着现代军事技术的发展，越来越多的防空导弹武器系统采用复合制导体制。捷联惯导+目标信息指令修正+主动雷达末制导是一种先进复合制导体制。导弹雷达导引头在制导末段开机截获目标，能否截获目标是系统最终能否命中目标的重要前提，因此分析各种误差源[1]对中、末制导交班概率的影响[2]，协调并分配相关分系统技术指标，就成为武器系统设计的一项重要工作。

本文基于上述的复合制导体制，建立了武器系统模型，分析各种误差源对中、末制导交班概率的影响，并在建立系统模型的基础上进行了仿真分析。

1 武器系统末制导交接班模型

武器系统主战装备由探测传感器、火力分配车(集成中制导指令机)、导弹发射车(可配置多部)及导弹组成。

探测传感器探测空中目标的三坐标位置、速度等信息并上报火力分配车；火力分配车指控系统进行目标分配并控制导弹准备、发射；导弹在发射后利用捷联平台测量和计算自身运动参数，通过无线电通道接收地面指令机(集成在火力分配车上)发送的目标更新信息指令，计算出与目标的相对运动参数，以一定的导引律飞向目标，当弹目距离一定时，导引头开机截获目标[3]，成功截获后即可转入末制导。系统工作原理如图1所示。

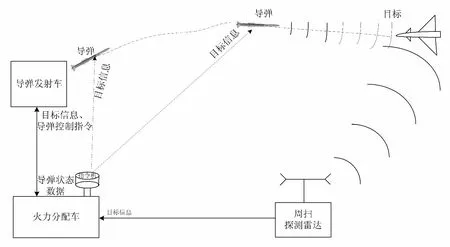
图1 武器系统工作原理

为了便于建模，提出以下假设：

1)中制导数据链路稳定可靠，导弹可接收每一帧制导数据；

2)导弹末制导寻的器框架角很大，可偏离弹轴方向进行任意指向预置；

3)导弹末制导寻的器视场为圆锥形，作用距离为Rsmax，视场角度为φsmax；

4)交接班时，弹上计算机需要根据导弹和目标位置计算出导引头波束指向[4]。假设目标真实位置为T,雷达测量点位置T′；导弹真实位置为M,导弹捷联惯导解算的导弹位置为M′；M′T′为导弹根据弹目位置计算的波束预置的指向；MTT为雷达波束的实际指向，假设导弹姿态无误差，其与M′T′平行；RTh为交接时刻导弹目标相对距离；σTh为交接时刻目标点的航向视线角偏差；qTh为交接时刻目标点的俯仰视线角偏差。

对于主动雷达导引头，目标的截获含目标的距离截获、角度截获和速度截获。导引头截获目标概率Pm为

Pm=PDPαPv

(1)

其中，PD为距离截获概率，在弹载设备工作正常条件下通常认为等于1；Pα为角度截获概率；Pv为速度截获概率，可以忽略此概率的影响，直接取1。

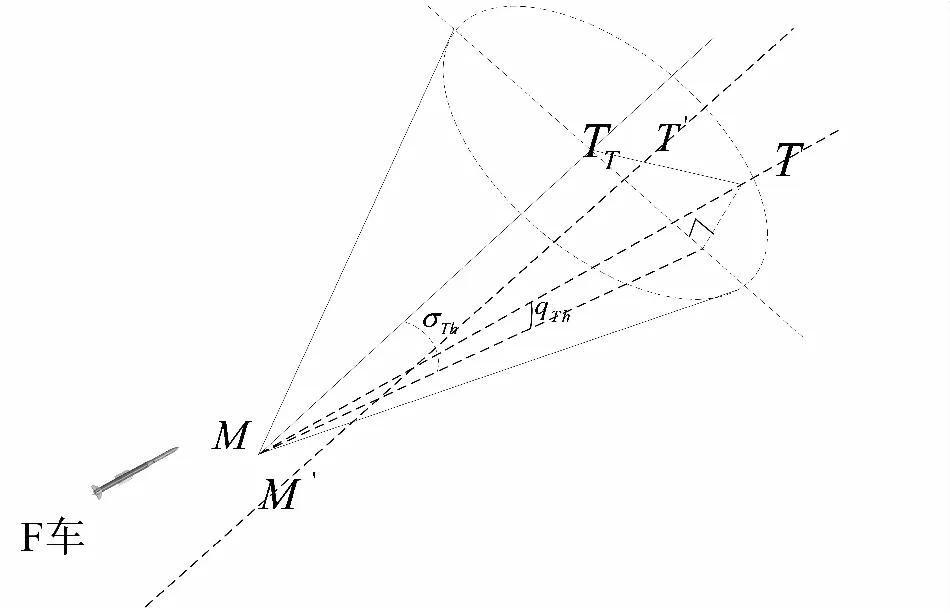
图2 中、末制导交接班模型

2 中末制导交接班的主要误差源分析及仿真设计

在不考虑导弹姿态误差的前提下，影响中末制导交接班的因素主要有目标位置精度、捷联惯导解算的导弹位置精度(内弹道精度)以及寻的器指向预置精度[5]。通常情况下，寻的器指向预置精度较高，可忽略不计。

影响目标位置精度的主要因素包括：

1)探测平台的定位定向误差；

2)发射平台的定位误差；

3)探测平台对目标的测量误差(包含调平带来的误差)；

4)目标机动误差(暂不考虑)；

5)影响导弹捷联惯解算的导弹位置精度主要因素包括：导弹初始对准误差，包括发射平台寻北误差、装配误差(含惯导与发射架安装误差、发射筒与发射架安装误差、导弹与发射筒安装误差等)；

6)弹载惯性器件的测量误差，主要包括加速度计、陀螺的测量误差。

随着惯性器件及相关算法的发展，对于飞行时间较短的中近程导弹弹载惯性器件的测量误差带来的捷联惯导解算误差可忽略不计。

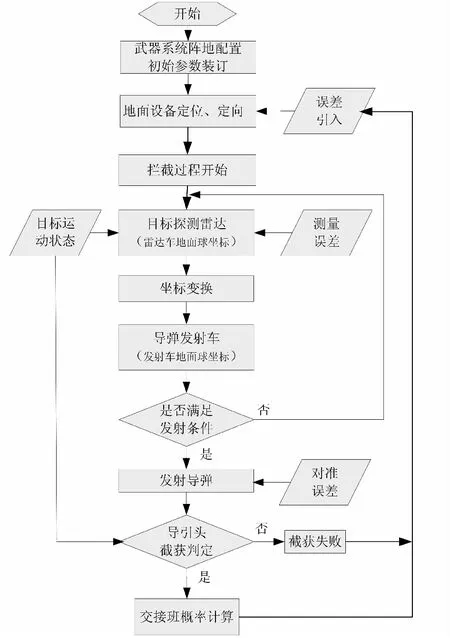
图3 中末制导交班误差累积过程

采用蒙特卡洛(Monte Carlo)方法，对交班概率进行分析。具体分析过程主要包含4个步骤：

1)根据设定作战场景，产生目标相对于雷达的真实坐标，根据作战的实际流程，在数据传输环节上引入随机生成的误差，计算目标真值和无线电修正信息；

2)根据无线电修正信息和设定的遇靶距离，计算导弹发射时机，引入随机生成的误差，然后计算到交班位置时导弹通过捷联惯导系统获得自己的位置、速度和姿态信息及这些信息的真值；

3)根据前两步的结果，计算是否满足成功交班条件；

4)多次重复1～3步，统计成功交班概率。

主要误差模型如下：

1)平台定位误差：圆概率分布；

2)平台定向误差：高斯随机分布；

3)雷达测量误差：高斯随机分布(加噪声后滤波处理，符合实际)；

4)装配对准误差：取指标最大值。

3 仿真分析

在不同系统误差的配置下，使遭遇点距离发射车基本一致，采用Monte Carlo方法进行100次仿真，统计分析各种状态下的交接班概率。

从表1中分析可以看出，相同条件下，目标角度测量误差、导弹对准误差及雷达车寻北误差是影响交接班概率主要误差源；载体的定位误差、目标距离误差对交接班概率影响不大。

相同条件下，导引头威力越远、波束越宽，波束空间覆盖区域越大，交接班概率越高，对地面设备误差精度要求越低。

表1 不同条件下仿真结果

序号12345678阵地配置两车距离/km000000010F车方位角/(°)00000000定位误差/m555520555高程误差/m1010101020101010S车寻北误差/(°)0.120.120.120.120.120.30.120.12F车寻北误差/(°)0.060.060.060.060.060.20.060.06开机时目标与S车距离/km54.554.554.554.554.554.554.564.3

续表

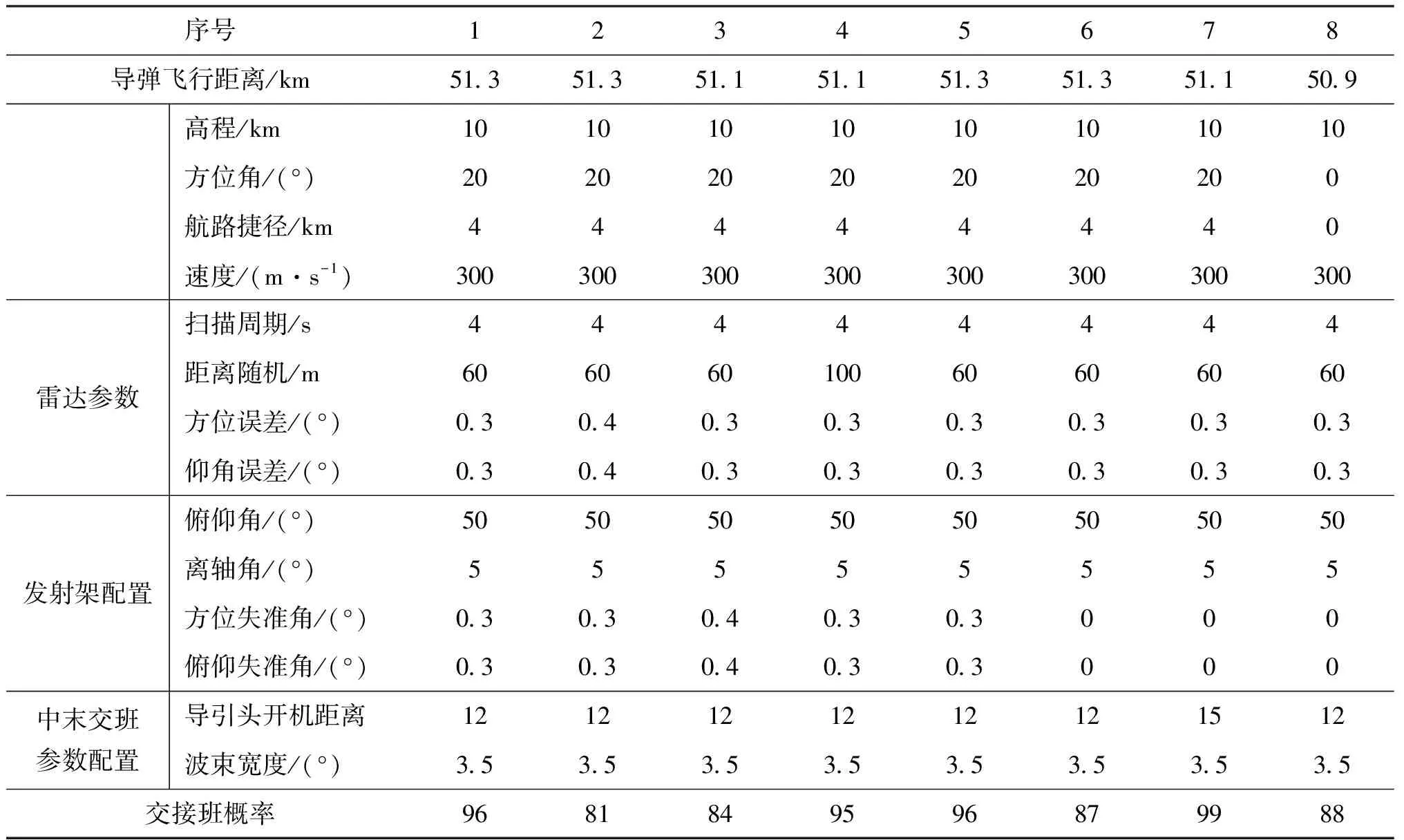
序号12345678导弹飞行距离/km51.351.351.151.151.351.351.150.9高程/km1010101010101010方位角/(°)202020202020200航路捷径/km44444440速度/(m·s-1)300300300300300300300300雷达参数扫描周期/s44444444距离随机/m60606010060606060方位误差/(°)0.30.40.30.30.30.30.30.3仰角误差/(°)0.30.40.30.30.30.30.30.3发射架配置俯仰角/(°)5050505050505050离轴角/(°)55555555方位失准角/(°)0.30.30.40.30.3000俯仰失准角/(°)0.30.30.40.30.3000中末交班参数配置导引头开机距离1212121212121512波束宽度/(°)3.53.53.53.53.53.53.53.5交接班概率96 81849596879988