基于函数“拐点”和“间断点”解构多过程物理量连续性和突变性
——变力作用下承递性物理事件中模型建构的教学思考
2020-05-07杨远萍
高 翔 杨远萍
(山东省青岛第一中学 266002)
模型建构是指在物理情景中依据已有经验和认知,对面临的物理情景进行问题抽象,构建问题本质图景,充分发挥学习者的心智模式,用简化的方式突出主要因素摒弃次要因素,将研究客体确立为理想化模型,运用数学符号、公式、图形、图像或者图表进行表征,通过分析与归纳,进行逻辑推理,形成科学认识的过程.它是科学思维的核心要素,因此模型建构教学的策略称为学科核心素养教育的重要目标.
承递性发生的多物理事件,由于约束条件或受力特征的变化,有些物理量保持连续性变化,体现为物理量的守恒性,因变量随自变量变化的这一规律体现为函数的连续性.有的则因为约束条件或受力特性的突然改变,有些物理量突然变化,使得连续变化的函数出现间断,成为非连续性函数,而另外一些物理量却依然守恒,向下一物理过程进行传递.如何凸显外界约束或者受力特征的跃变,表征物理量的间断和某种物理量守恒性,这对于模型建构和模型识别具有重要的意义.
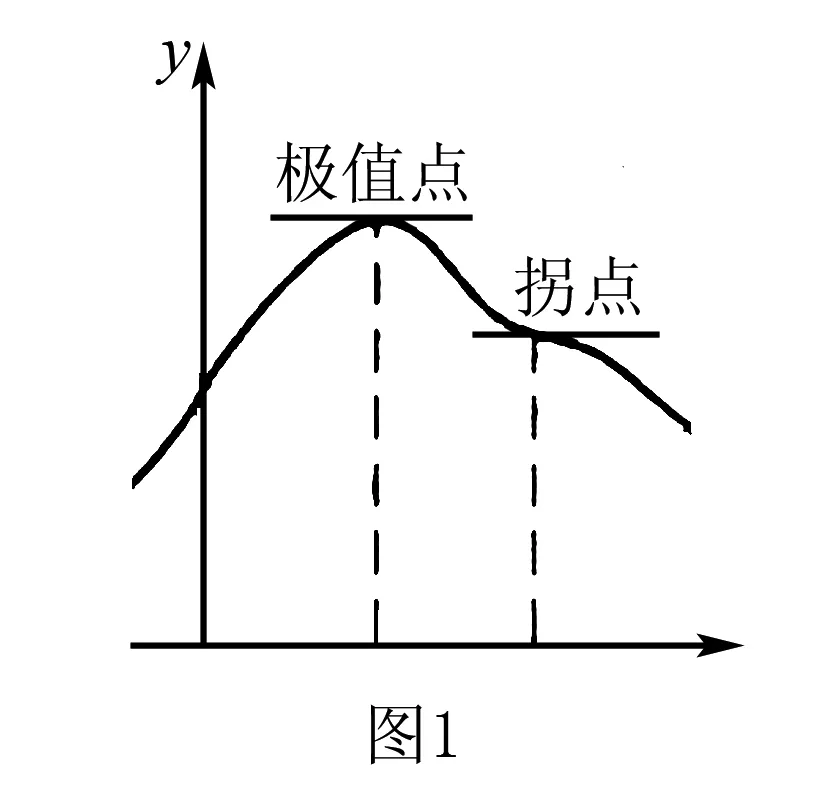
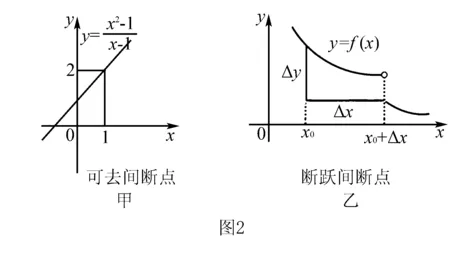
第三类是前后状态参量因受力或者约束条件突然改变,使得物理事件出现断裂,某些物理量在此出现间断不再顺延性发生,这一点成为突变点.虽然某些物理量守恒向下传递,但另外一些物理量因突然性变化而不再守恒,呈现出断崖式的跃升或突降,函数在此点不再连续成为间断点.像轻质细绳猛然绷紧的瞬间、非弹性碰撞……等.依据间断点左右两侧是否有导数和导数是否相等来分类,如果左右导数相等,该点称为可去间断点,如图2(甲)所示.如果左右导数存在但不相等,如图(乙)所示称为跳跃间断点.
从函数的连续性和间断性的视角对承递发生的多物理过程分类,凸显那些运动状态参量顺延,那些运动状态参量突变,有助于我们全程的角度还是分段的角度建构过程模型具有决定性的作用,这也是科学思维培育的主要途径.
一、同一物理事件中处于空间位置点函数约束下运动的合成
外力为空间位置的函数F(x)作用下,运动状态参量在这一物理事件中非线性变化,尽管物理量表现为连续性,但因外力和约束条件的变化使得不同物理事件呈现不同的单调性,衔接处称为物理事件的拐点.
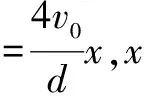
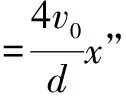
2.物理过程模型建构的错误导致错解.船在水的冲击下同时参与了两个分运动而表现为对岸的合运动.距离近岸距离的不同水流速分布不同,不能凭借v水∝x就简单视为沿水流方向上船做初速度为零的匀加速直线运动.答案为AD
二、同一物理事件中受到空间位置点函数F(x)变力作用下状态量的求解
物体受到的外力随空间位置的不同而变化,而这种变化体现为空间位置的连续性,即力是空间位置的点函数F(x).由于不同位置处合外力不同,速度变化的快慢呈现差异,力在空间位置上累计效果—功能思维就成为解决问题的关键.力在空间元位移内的积分就成为求解该问题的关键.
1.F(x)为线性变化的作用力
例题2如图3甲所示,在水平地面上放置一个质量为m=4 kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力F随位移x变化的图像如图3乙所示.已知物体与地面之间的动摩擦因数为μ=0.5,g=10m/s2.求:
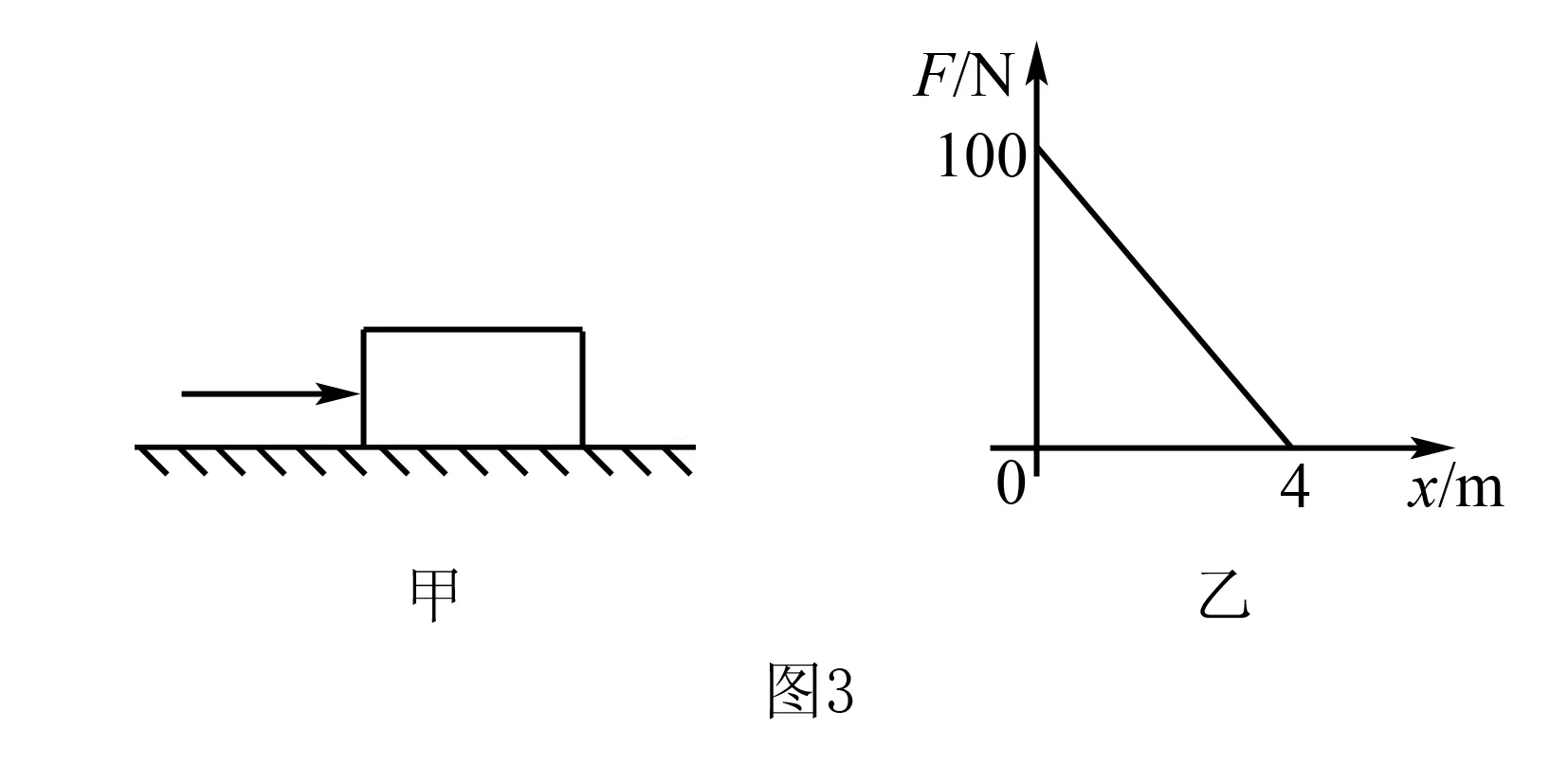
(1)运动过程中物体的最大加速度为多少?
(2)距出发点多远时物体的速度达到最大?
(3)物体在水平面上运动的最大位移是多少?
模型建构中困惑点分析过程模型建构的合理性决定了求解方法的科学性,其关键是对变力作用下物体运动状态的判断和力作用效果的描述,为此呈现如下的困惑:
1.从力和运动角度分析物理过程是求解前提,判明各过程的受力特征和运动特性是解决问题的根本.
2.表征变力的作用效果是解决问题的关键.从力的瞬时性上分析物理过程求解最大加速度和最大速度.从力的空间位置的积累效应求解发生的位移.
解析由牛顿第二定律得F-μmg=ma,当F=100N时物体所受的合外力最大,解得a=20m/s2;
(2)由图像,推力F随位移x变化的关系:F=100-25x,当F=μmg,解得x=3.2m;
2.F(x)为振荡性变化的作用力
例题3如图4甲所示,一固定在水平面上倾角θ=37°、高h=0.3m的绝缘斜面.一视为质点质量为m=1kg、带电荷量q=+0.02C的物块放在斜面顶端,距斜面底端L=0.6m处有一竖直放置的绝缘光滑半圆轨道,半径为R=0.2m半圆轨道底端有一质量M=1kg可视为质点的绝缘小球,半圆轨道底端与斜面底端之间存在如图4乙所示的变化电场(水平向右为正方向),图4乙中O点对应坐标原点,虚线与坐标轴围成的图形是椭圆一部分(椭圆面积公式S=πab,a、b分别为半长轴和半短轴).现给物块一沿斜面向下的初速度v0,物块运动到半圆轨道处与小球发生对心弹性碰撞,不计物块经过斜面底端时能量损失,已知物块与斜面、水平面间的动摩擦因数均为μ=0.5,g=10m/s2,sin37°=0.6cos37°=0.8.
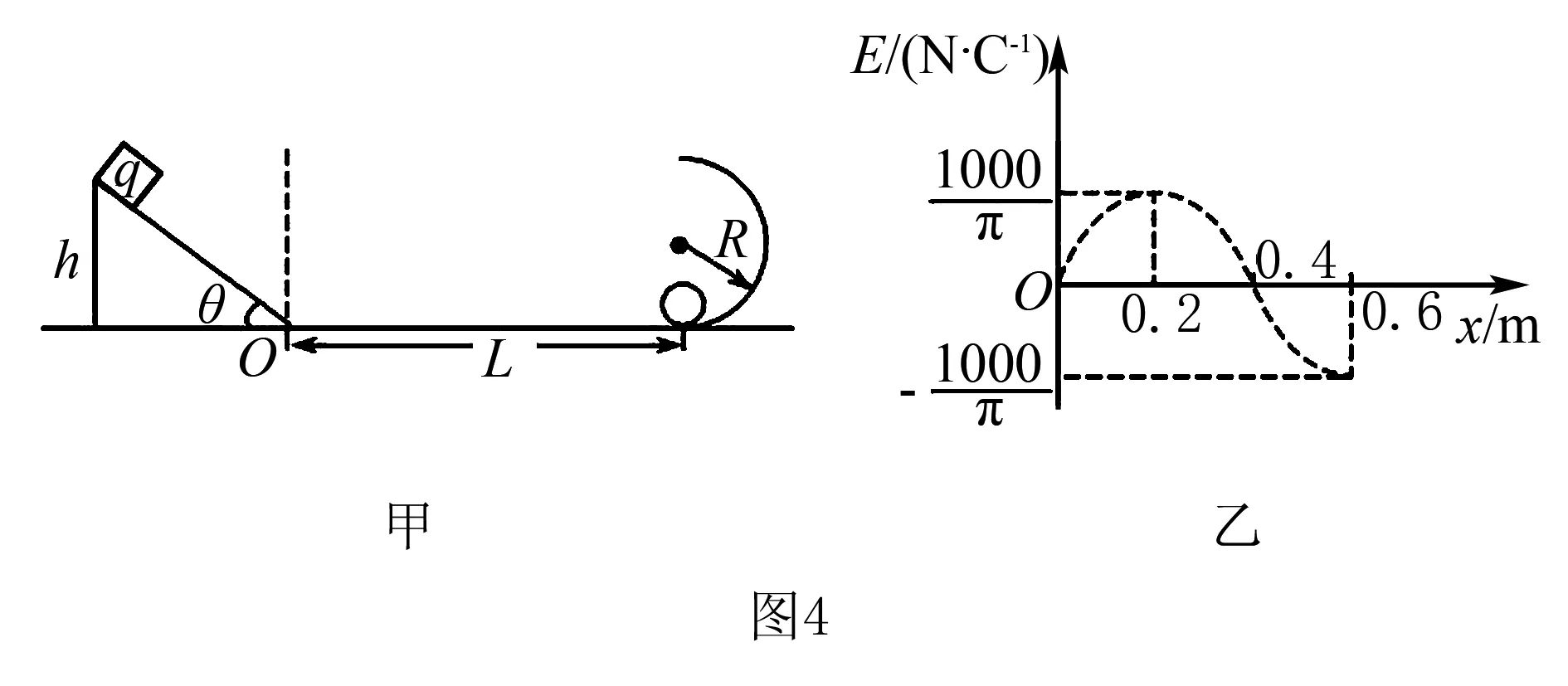
(1)若小球不脱离半圆轨道,求物块在斜面顶端释放的初速度v0的范围;
(2)若小球能通过最高点,并垂直打在斜面上,求小球离开半圆轨道时的速度大小及小球打在斜面上的位置;
模型建构中心智模式的障碍分析
针对各物理过程受到的约束限制和所受外力的特征确定运动规律,建构呈递发生的物理过程模型是解决问题的关键,量度各力做功,分类讨论“小球不脱离半圆轨道”情况是解决此问题的切入点.
1.从力和运动的角度分析呈递发生的多方物理过程,建构过程模型是解决问题的前提.
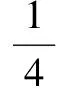
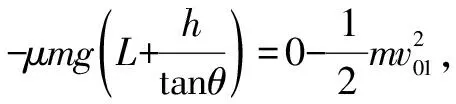
分情况判断是分类讨论的关键.“不脱离圆形轨道”分到达与半圆形轨道圆心等高处和恰好到达半圆形轨道最高点两种情况.
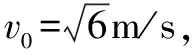
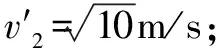
综上述物块在斜面顶端释放的初速度范围为
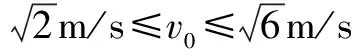
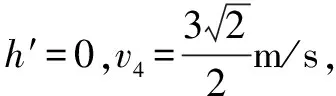
三、同一物理事件中受F(t)变力作用下状态量的求解
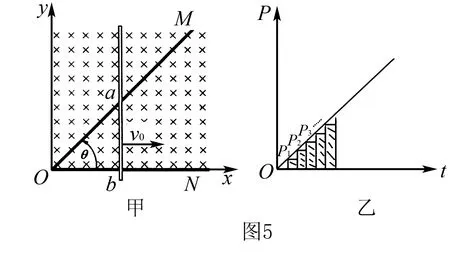
例题4如图5甲所示,顶角θ=45°的金属导轨MON固定在水平面内,导轨处在方向竖直,磁感应强度为B的匀强磁场中,一根与ON垂直的导体棒在水平外力作用下的恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均为r,导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触,t=0时导体棒位于顶角处.求:
(1)t时刻流过导体棒的电流强度I和电流方向;
(2)导体棒做匀速直线运动时水平外力F的表达式;
(3)导体棒在0-t时间内产生的焦耳热Q;
(4)若在t0时刻将外力F撤去,导体棒最终在导轨上静止时的坐标x;
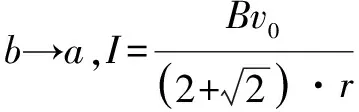
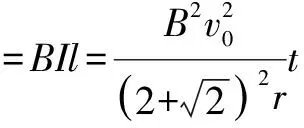
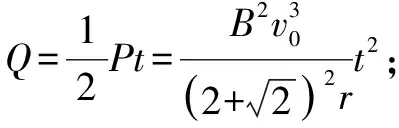
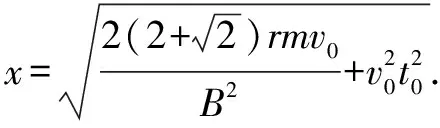
四、从“拐点”的角度揭示承递性物理事件连接处物理量的顺承变化
承递发生的多物理事件连接处,由于外在约束或者受力特征的突然变化引起某种物理量开始改变而原先变化的物理量保持不变,因不同的变化规律前后物理过程呈现为不同的单调性,这一承接点我们称之为函数的“拐点”.
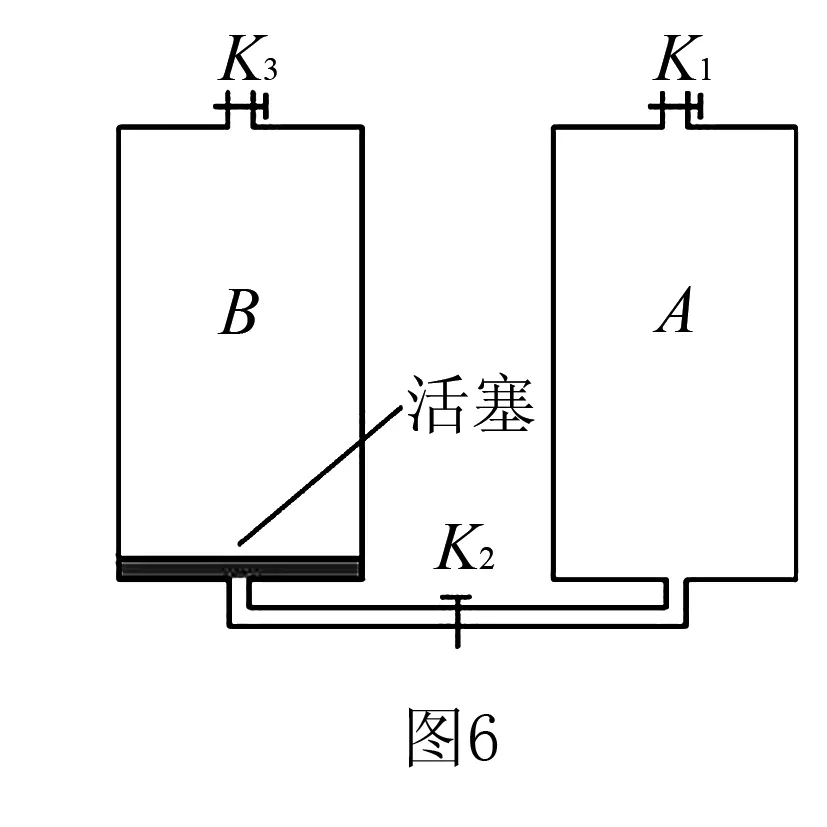
例题5如图6,容积均为V的汽缸A、B下端有细管(容积可忽略)连通,阀门K2位于细管的中部,A、B的顶部各有一阀门K1、K3;B中有一可自由滑动的活塞(质量、体积均可忽略).初始时,三个阀门均打开,活塞在B的底部;关闭K2、K3,通过K1给汽缸充气,使A中气体的压强达到大气压p0的3倍后关闭K1.已知室温为27℃,汽缸导热.
(1)打开K2,求稳定时活塞上方气体的体积和压强;
(2)接着打开K3,求稳定时活塞的位置;
(3)再缓慢加热汽缸内气体使其温度升高20℃,求此时活塞下方气体的压强.
模型建构的路径分析物理事件1.关闭阀门K2和K3,B中气体状态参量未变,外部一定量的气体充入气缸A中,使得A气缸中的气体不再是原先的气体.充入气体后的A′才为后续物理事件的初始状态;
物理事件2.打开阀门K2,由于不计活塞质量,稳定时A与B中气压相等—这是不同系统的关联,即力学量的传递.活塞被上推至某一位置,设体积减少ΔV,A、B气压p1.
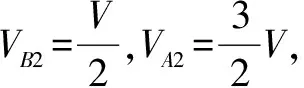
物理事件3.打开阀门K3,B中气体急剧外泄称为一个开放的系统,但活塞上升至何处?能否被推至气缸顶部?推至顶部是否与缸顶存在挤压?活塞与缸顶出现弹力是呈递发生物理事件的拐点.
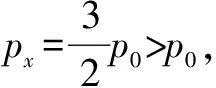
从函数连续性和间断性视角将物理事件划分为衔接性发生的物理事件和某种守恒量跃变的非连续性过程,不仅凸显先后物理过程连接处力和运动的特征,而且呈现延续发展的物理量和跃变的物理量,有助于过程模型的科学建构,有利于我们选择全程和分段的方法解决问题,这是科学思维培育的重要路径.
