一道最值问题的解题研究
2020-05-07刘显海汪应佳
刘显海 汪应佳
(江西省赣州市南康区第三中学 341400)
一、问题来源
题目已知m,n∈R,m+2n=2,则m·2m+n·22n+1的最小值为____.
二、问题解决
1.第一次改造
首先将要求最小值的式子写成整齐的对称形式:m·2m+n·22n+1=m·2m+2n·22n=x·2x+y·2y,其中x=m,y=2n,满足x+y=2.
这样,我们就把原来的题目改写成了一个等价的“新”题目:
变题1已知x,y∈R,x+y=2,则x·2x+y·2y的最小值为____.
下面给出基于“变题1”的两种完全不同的解法.
解法1(运用对偶配对方法及排序不等式思想)
记A=x·2x+y·2y,B=x·2y+y·2x,则有:
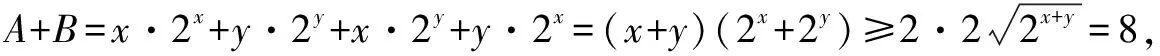
A-B=x·2x+y·2y-x·2y-y·2x=(x-y)(2x-2y)≥0.②
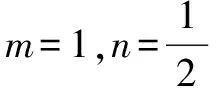
解法2(消元化为一次函数求导法)
由x+y=2得y=2-x,则求最小值的式子即y=x·2x+(2-x)·22-x.观察其结构易知函数y=f(x)的图象关于直线x=1对称,故下文的讨论以x=1为临界点来展开讨论.
对函数求导,得:
f′(x)=[2x+x·2xln2]+[-22-x+(2-x)22-xln2·(-1)]
=(2x-22-x)+[x·2x-(2-x)·22-x]ln2.
(1)当x>1时,易知2x-22-x>0,x·2x-(2-x)22-x>0,所以f′(x)>0;
(2)当x<1时,易知2x-22-x<0,x·2x-(2-x)22-x<0,所以f′(x)<0;
(3)当x=1时,易知f′(x)=0.
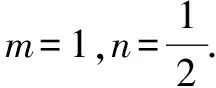
注:(1)以上两种解法充分利用了将问题改造后形成的对称性,分别借助于对偶配对及消元求导方法,顺利求出了最小值;
(2)以上两种解法从某种意义上来说都不“简单”,但无论如何,这两种解法都还在高中生能够接受的范围内.
2.第二次改造
以下的三种解法是基于“从实数到非负实数”的思想进行改造.从题目出发我们进一步得出更多的有用信息,即:在条件x+y=2下,x·2x+y·2y的最小值必在x≥0且y≥0时取得.事实上,若不然,不妨设x<0,则y>2,因此:
x·2x+y·2y>x+(2-x)×4=8-3x>8.
而取x=0,y=2可得x·2x+y·2y=8,故可知最小值不可能在x<0时取得.由此,题目可以在“变题1”的基础上进一步改造为:
变题2已知x+y=2,x≥0且y≥0,则x·2x+y·2y的最小值为____.
接下来的解法就直接考虑这一问题了.
解法3(凸函数及Jensen不等式法) 记f(x)=2x,易知其为凸函数,因此对于任意非负实数λ1,λ2,若λ1+λ2=1,则有:
λ1f(x1)+λ2f(x2)≥f(λ1x1+λ2x2).
应用上述不等式,可得:
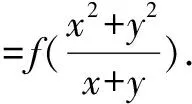
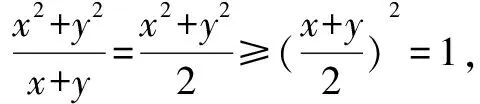
由③和④,得:
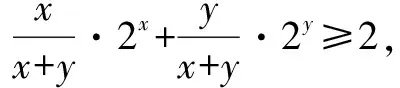
解法4(另一个凸函数方法)记f(x)=x·2x,则f′(x)=2x+x·2xln2,f″(x)=2xln2+(2x+x·2xln2)ln2>0,故可知函数f(x)=x·2x为凸函数,所以
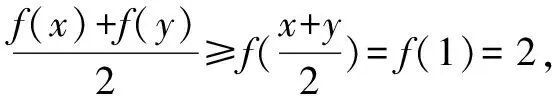
解法5(Lagrange乘数法)记f(x,y,λ)=x·2x+y·2y+λ(x+y-2),则
fx=2x(xln2+1)+λ=0, ⑤
fy=2y(yln2+1)+λ=0, ⑥
fλ=x+y-2=0.⑦
因为2x(xln2+1)是递增的,而由⑤和⑥两式可得2x(xln2+1)=2y(yln2+1),所以x=y.再结合⑦可得x=y=1,此即取得最小值的条件,代入计算易得最小值为4.
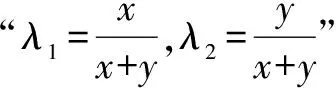
(2)严格来说,以上这三种解法都称不上“初等”,因为分别借助了高等数学里的凸函数理论和多元函数求最值的Lagrange乘数法.但是,凸函数概念和Jensen不等式实际上早已是中学数学里的“常客”,例如高中数学教材《必修1》的复习题中曾两次提到有关凸函数的不等式,而在各类考试中,更是不乏有关凸函数的不等式的身影.
三、题外话:能猜出答案吗?
以上的两次改造、五种解法都是以“解答题”的严格要求来解决这样一个“填空题”,从数学所追求的的严谨性、逻辑性而言当然无可厚非.但是,作为一个考试中的一个“填空题”而言,上面的五种解法中的任何一种其实都是不太合适的.解法1、3确实简易,却太过巧妙,技巧过高;解法2、4、5计算量太大,求导、整理化简难度不小.就题论题,从应试的角度看,我们难道真的需要花大把时间来解这样一个“小题”吗?其实,这个题目在改造为“变题1”后,就应该完全可以“猜出”而且“猜对”答案,注意条件“x,y∈R,x+y=2”和要求最小值的式子“x·2x+y·2y”都是关于两个变量“x,y”完全对称的,因此最小值必定在其相等时取得,因为对称意味着两者的地位完全相等.答案得以轻松“猜出”!
