应用气体实验定律求解变质量问题

赵生武

(甘肃省兰州市永登县第一中学 730300)

气体实验定律是热学部分内容在历年全国卷高考中唯一的Ⅱ级要求考点，试题往往以计算题的形式考查一定质量理想气体在某一变化过程中状态参量的变化.然而在给容器充气、容器漏气、气体分装及气体压缩等情境下，伴随着气体质量的变化，借助这类情境考查学生科学思维能力和运用所学知识解决实际问题能力是近年高考命题的趋势.那么，如何正确地求解变质量问题？笔者结合自己的教学实践做以下的归类剖析.

一、充气问题

充气问题中，相对于容器而言，气体的质量增大.假想用一个无形的容器把待充入的气体收集起来，原容器中的气体和假想容器中气体的整体在状态变化过程中质量保持不变.所以，把这一整体作为研究对象，就将变质量问题转化为一定质量的问题.

例1 一个篮球的容积是2.5 L，用打气筒给篮球打气时，每次把105Pa的空气打进去125 cm3.如果在打气前篮球内的空气压强也是105Pa，那么打30次以后篮球内的空气压强是多少？(设打气过程中气体温度不变)

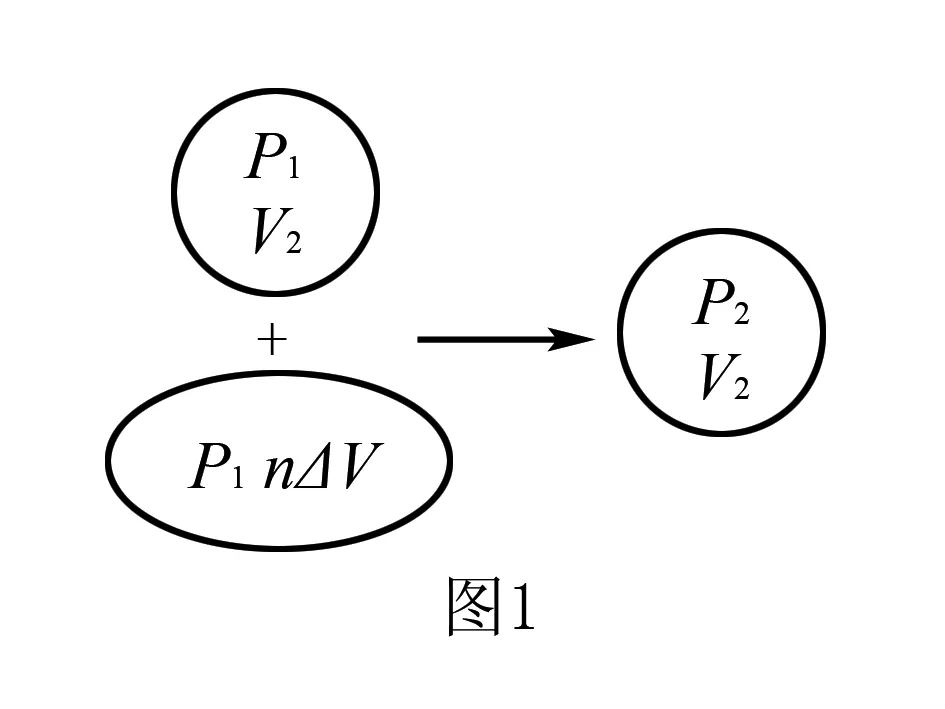
解析将篮球内原有气体和待充入气体的整体为研究对象.

设篮球容积为V2，总的气体体积为V1，则V1=V2+n·ΔV=6.25L.

压强为p1=105Pa时，体积V1=6.25L

压强为p2时，体积V2=2.5 L

由玻意耳定律得：p1V1=p2V2，联立解得：p2=2.5×105Pa

评析将篮球内的原有气体和被充入的气体整体作为研究对象是求解问题的关键.思维导图如图1所示.

二、用气或漏气问题

容器用气或漏气的过程中，容器中气体的质量不断减小，无法直接用气体实验定律求解.假设被用或漏出的气体“出而不走”，被一个无形的大容器收集起来，则容器内剩余气体和已用(或已漏)气体的总质量保持不变.可以将容器内剩余气体和已用(或已漏)气体的整体作为研究对象，使变质量问题转化为一定质量气体状态变化问题.

例2 [2016·全国卷Ⅰ]一氧气瓶的容积为0.08 m3，开始时瓶中氧气的压强为20个大气压.某实验室每天消耗1个大气压的氧气0.36 m3.当氧气瓶中的压强降低到2个大气压时，需重新充气.若氧气的温度保持不变，求这瓶氧气重新充气前可供该实验室使用多少天.

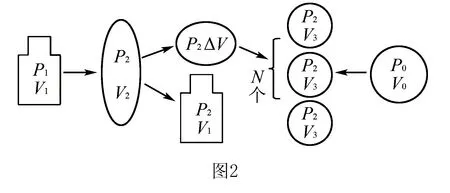
解析将原有氧气瓶中的氧气作为研究对象，设压强为p1(20个大气压)时，体积为V1(0.08 m3)；压强为p2(2个大气压)时，体积为V2.由玻意耳定律得：p1V1=p2V2

设被用去氧气在压强p2(2个大气压)时的体积为ΔV，则ΔV=V2-V1.

每一天消耗的氧气为研究对象，设压强为p0(1个大气压)时，体积为V0(0.36 m3)，压强为p2(2个大气压)时，体积为V3，则p0V0=p2V3.

评析1.运用“出而不走”的假设思想，将原有总的气体为研究对象，将变质量问题转化为一定质量问题.2.“中间状态”(压强为2个大气压)的确定是分析问题的桥梁.将原有总氧气、被用去氧气和一天消耗的氧气的体积均转化为中间状态的体积，便于求解可供使用的天数.思维导图如图2所示.

三、气体分装问题

将一个大容器中的气体分装到多个小容器中时，大容器中的气体质量减小，属于变质量问题.若将大容器中的气体和多个小容器中原有气体的整体作为研究对象，整体的质量不变，属于一定质量问题.

例3 某容积为20 L的氧气瓶装有30 atm的氧气，现把氧气分装到容积为5 L的小钢瓶中，使每个小钢瓶中氧气的压强为5 atm，若每个小钢瓶中原有氧气压强为1 atm，问能分装多少瓶？(设分装过程中无漏气，且温度不变)

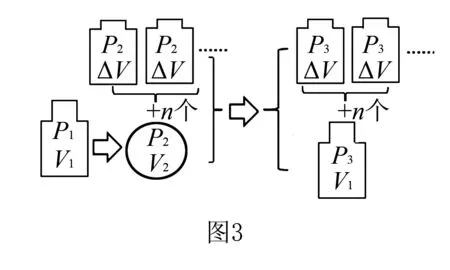
解析将分装前氧气瓶中的氧气作为研究对象，设在压强p1=30atm时，体积V1=20L，压强p2=1atm时，体积为V2，则由玻意耳定律得：p1V1=p2V2，解得V2=600L.将氧气瓶中氧气和所有小钢瓶中的氧气的整体作为研究对象(设分装n瓶)，压强p2=1atm时，体积V2′=V2+5n，压强p3=5atm时，体积为V3=V1+5n，由玻意耳定律得：p2V2′=p3V3，联立解得：n=25(瓶).

评析1.将氧气瓶中氧气和所有小钢瓶中的氧气的整体作为研究对象，使变质量问题转化为一定质量问题.2.设定中间状态(压强p1=1atm)，应用玻意耳定律，把氧气瓶中氧气状态参量转化为中间状态，将氧气整体转化为同一压强，便于分析整体的状态变化.3.分装前氧气整体的体积包括氧气瓶中氧气在中间状态(压强p2=1atm)下的体积和所有小钢瓶的容积之和；分装后氧气体积包括氧气瓶的容积和所有小钢瓶的容积之和.思维导图如图3所示.

四、气体压缩问题

用压缩机将几个小容器中的气体压入大容器时，大容器中的气体质量不断增加.若将大容器中原有气体和待压入的所有小容器中的气体整体作为研究对象，整体在状态参量发生变化时总质量不变.

例4 [2019·全国卷Ⅰ]热等静压设备广泛用于材料加工中.该设备工作时，先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中，然后炉腔升温，利用高温高气压环境对放入炉腔中的材料加工处理，改变其性能.一台热等静压设备的炉腔中某次放入固体材料后剩余的容积为0.13 m3，炉腔抽真空后，在室温下用压缩机将10瓶氩气压入到炉腔中.已知每瓶氩气的容积为3.2×10-2m3，使用前瓶中气体压强为1.5×107Pa，使用后瓶中剩余气体压强为2.0×106Pa；室温温度为27℃.氩气可视为理想气体.

(1)求压入氩气后炉腔中气体在室温下的压强；

(2)将压入氩气后的炉腔加热到1227℃，求此时炉腔中气体的压强.

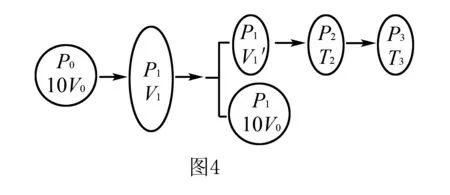
解析(1)10瓶氩气整体为研究对象，压强p0=1.5×107Pa时,体积10V0=10×3.2×10-2m3，压强p1=2.0×106Pa时,体积V1，由玻意耳定律得：10p0V0=P1V1，解得V1=2.4m3.

被压入炉腔中的氩气为研究对象，设压强p1=2.0×106Pa时，体积V1′=(V1-10V0) ，压入后室温下的压强为p2，体积V=0.13m3，则p1V1′=p2V，解得p2=3.2×107Pa.

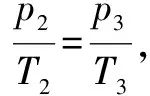
解得p3=1.6×108Pa .

评析1.由于炉腔抽真空，所以待压入的10瓶氩气为研究对象，压入后包括炉腔内氩气和瓶中剩余氩气两部分.

2.氩气压入之前先假设所有氩气整体发生等温变化，求出压强为p1=2.0×106Pa时的体积V1，此状态下将体积V1′=V1-10V0的氩气压入炉腔，这部分氩气先发生等温变化，后发生等容变化，分别求出室温下的压强和加热后的压强.思维导图如图4所示.

通过以上剖析可以看出，应用气体实验定律处理变质量问题时，巧妙确定研究对象，将变质量问题转化为一定质量问题是分析问题的关键；假设某一中间状态，分析中间状态下的参量是求解问题的桥梁.分析问题时画出思维导图，能够更加清晰地理解气体状态变化过程，便于选用合适的气体实验定律列方程求解.