基于人工神经网络的压水堆燃料破损状态监测

肖 维，尹楚轩，李宏轩，董 冰，尹俊连，王德忠

(上海交通大学 核科学与工程学院，上海 200240)

燃料元件包壳是反应堆安全的重要屏障[1]，它的状态与反应堆运行安全密切关联。反应堆运行过程中，在定位格架磨蚀、异物冲击等因素作用下，燃料包壳有可能发生破损[2]，破损发生后包壳间隙中的放射性裂变产物会通过破损释放到冷却剂中，引起一回路剂量上升，从而对核电站的安全、经济性造成恶劣影响。因此，燃料包壳的破损问题是国际上一重要的研究课题[3-5]，有必要在反应堆运行过程中快速、准确地通过一回路冷却剂中裂变产物比活度判断燃料包壳是否发生破损以及燃料包壳的破损程度[6-7]。

现有方法一般在一级动力学释放模型基础上[8]，基于冷却剂中两种裂变产物比活度的比值预测燃料包壳破损状态，例如131I/133I、133Xe/135Xe的比值判断燃料包壳的破损程度；134Cs/137Cs的比值判断破损燃料棒的燃耗[9-11]，不同学者关于比活度比值范围对应的包壳破损状态并无统一意见，并且在燃料包壳破损预测中存在误判[12]。

针对上述问题，本文使用Booth模型[13]和一级动力学模型[8]建立不同包壳破损程度下冷却剂中裂变产物比活度的数据库，使用该数据库构建人工神经网络，由一回路冷却剂裂变产物比活度判断燃料棒包壳是否破损及其破损等级，并与现有的碘同位素比值法进行比较，旨为燃料包壳破损预测提供一种新方法。

1 模型建立

1.1 裂变产物释放模型

裂变产物i在燃料芯块中产生和消失的平衡方程为：

(1)

式中：Xi为核素的原子密度，cm-3；NU为UO2的核子密度，cm-3；σf为UO2的微观裂变截面，b(1 b=10-28m2)；Yi为核素i的裂变产额；Iji为核素j到核素i的分支比；λj为核素j的衰变常量，s-1；φ为平均中子注量率，cm-2·s-1；fji为j吸收中子变为i的份额；σk为平均中子吸收截面，b。

裂变产物从燃料芯块到包壳间隙的释放率使用Booth模型计算，该模型将燃料芯块内的UO2晶粒近似为球形，以1个燃料小球为控制体建立球坐标系下的扩散方程：

(2)

式中：Bi为裂变产物i在燃料小球内的产生速率，cm-3·s-1；D为裂变产物在UO2晶粒内的扩散系数，cm-2·s-1。

通过求解方程(2)可得到裂变产物在燃料芯块的释放产生比(R/B)：

(3)

式中：Ri为裂变产物i在燃料小球内的释放速率，cm-3·s-1；a为UO2晶粒的平均直径，cm。

燃料包壳间隙中的裂变产物i浓度NGi的平衡方程为：

(4)

式中，νi为裂变产物从包壳间隙到一回路的逃脱率系数，s-1。

一回路中的裂变产物i浓度NCi的平衡方程为：

(5)

式中：qi=Q/W·ηi+βi+L/W为一回路中裂变产物i的消失率，s-1，其途径有净化、调硼补水、泄漏等；Q为冷却剂总流量，m3·s-1；W为冷却剂总体积，m3；ηi为净化效率；βi为调硼补水导致的裂变产物消失率, s-1；L为冷却剂泄漏流量，m3·s-1。

燃料元件加工过程中在包壳外表面存在沾污铀，沾污铀在反应堆运行过程中同样产生裂变产物释放到冷却剂中。沾污铀对一回路比活度贡献的裂变产物i浓度NTi的平衡方程为：

(6)

式中：φc为冷却剂中的平均中子注量率，cm-2·s-1；Yi为核素i的裂变产额；σf为UO2的微观裂变截面，b；ε为沾污铀的释放份额，基于保守假设，ε取值为0.5。

1.2 神经网络模型

本文使用Back Propagation(BP)神经网络建立包壳破损状态预测模型，BP神经网络是一种对连续非线性问题具有优异拟合能力的，采用误差反向传播算法的多层前馈人工神经网络。目前已证明，BP神经网络能以任意精度逼近任何非线性连续函数[14]，其结构如图1所示。

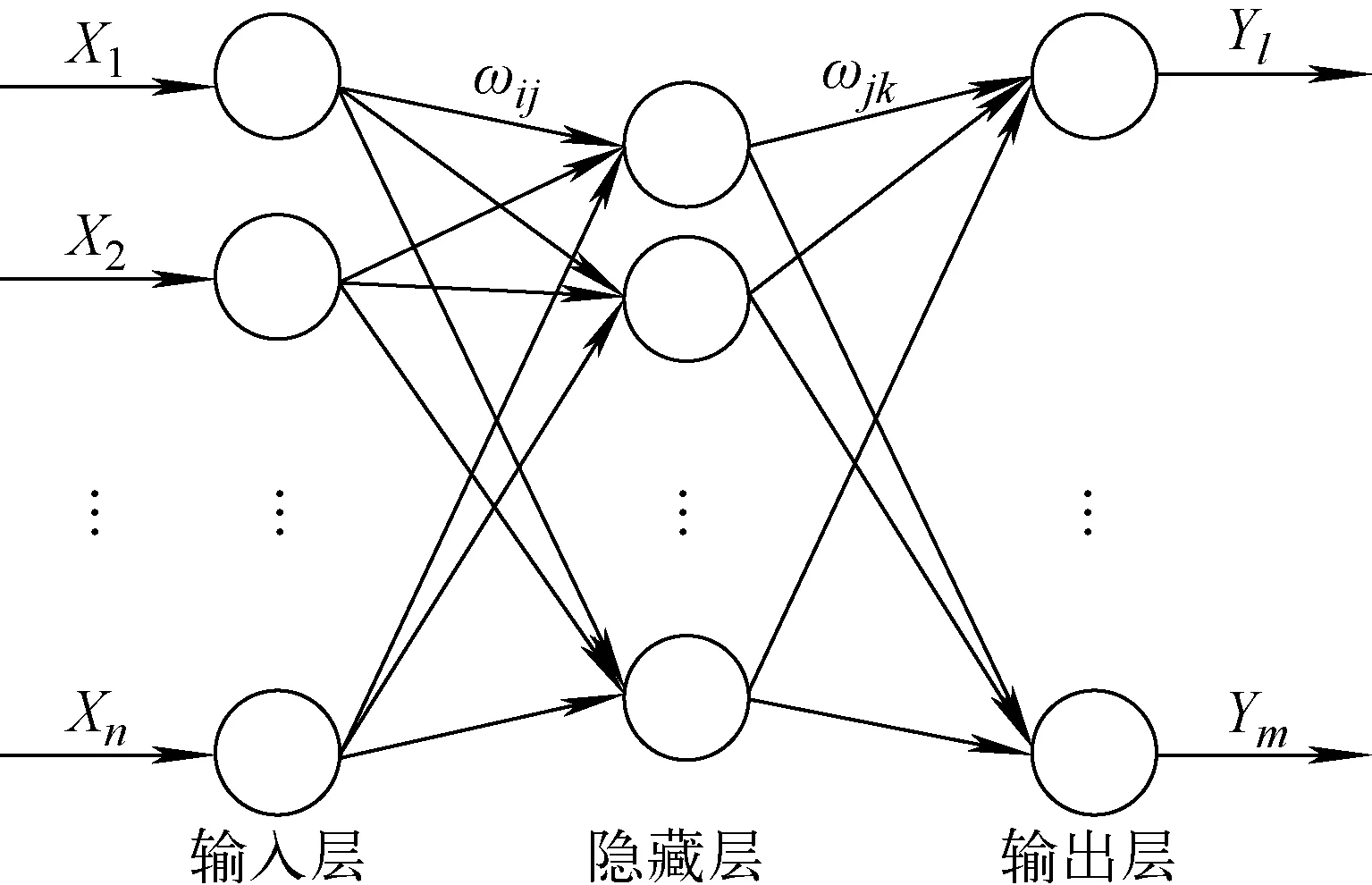
图1 3层BP神经网络原理框架图Fig.1 Principle framework of three-layer BP neural network

BP神经网络中隐藏层节点数量可使用经验公式确定[15]，m、n、l分别为输出层、输入层和隐藏层节点数：

l=

(7)

BP神经网络的激活函数选用Sigmoid函数：

(8)

BP神经网络在训练过程中一般使用梯度下降算法，权重ω沿梯度反向调整。但实际使用中，梯度下降算法收敛速度慢且易陷入局部最小值。相比梯度下降算法，Levenberg-Marquardt(L-M) 算法具有不易陷入局部最小值、稳定性高、收敛速度快的特点，故本文使用L-M算法训练BP神经网络，其权重更新规则为：

ωk+1=ωk-[JTJ+μI]-1Je

(9)

式中：J为Jacobian矩阵；I为单位矩阵；e为误差向量。

本文使用两个串联的BP神经网络，第1个用于判断包壳是否破损，第2个在包壳发生破损后判断包壳的破损等级。

2 判断包壳破损情况

2.1 训练神经网络

根据裂变产物正向释放模型，构建用于判断包壳是否破损的神经网络的训练集，设定19个不同的包壳破损时间，计算得到108s内23种裂变产物在冷却剂中的比活度作为训练集的输入向量，对应的输出向量破损时刻前为0，破损时刻后为1。根据式(7)，隐藏层节点数设定为9。

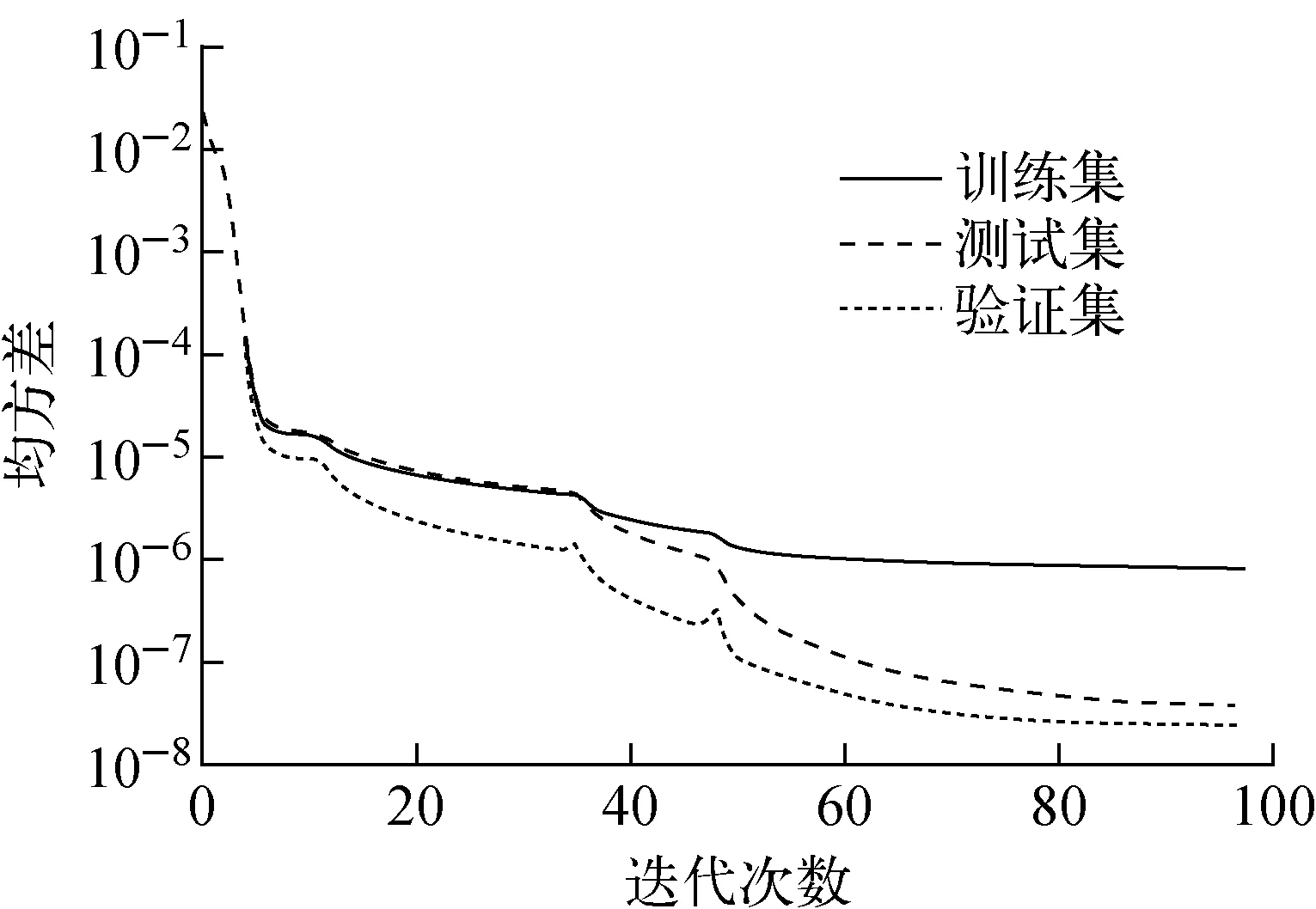
图2 包壳破损的神经网络均方差收敛图 Fig.2 Mean squared error of neural network for cladding failure

使用神经网络判断是否发生破损的阈值设置为0.5，即输出向量值小于0.5认为包壳未发生破损，输出向量值大于0.5认为包壳发生破损。图2为神经网络训练过程的残差曲线，神经网络能快速收敛到较低的错误率。测试结果表明，训练好的神经网络判断包壳破损状态的错误率为5.3×10-7。表1列出几个典型测试集中破损时间与神经网络反演结果的对比，神经网络能根据23种裂变产物的比活度判断包壳是否发生破损，因而可及时发现包壳破损。

表1 破损时间预测Table 1 Defect time prediction

2.2 敏感性分析

为测试所建立神经网络的健壮性，考察了数据扰动和特征核素的选取对神经网络预测结果的影响，并关于沾污铀质量、单棒功率两个因素对神经网络进行了敏感性分析。

给测试集分别增加5%、10%、30%的随机扰动，然后用神经网络进行反演，结果列于表2，神经网络对于有扰动的测试集预测效果很好，即使数据的随机扰动达到30%，预测误差仍在非常低的水平，错误率为2×10-4。

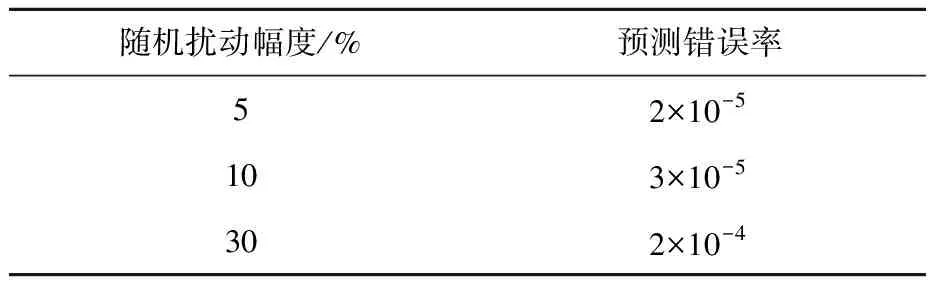
表2 神经网络对于有扰动的测试集的预测结果Table 2 Prediction towards perturbed test set by neural network

由于部分裂变产物半衰期短、特征γ射线能量较低，需对作为输入向量的核素进行进一步的筛选。表3列出考虑半衰期和特征γ射线能量筛选后作为燃料元件破损反演的关键核素。

根据式(7)，确定神经网络隐藏层节点数为5。经测试，该神经网络对于原训练集的状态的判断错误率为2.1×10-6，略高于使用23种特征核素训练得到的神经网络的错误率5.3×10-7，但仍属于极低的水平。即使仅选取6种特征核素作为输入向量，神经网络模型仍能以2.1×10-6的错误率准确反演包壳是否破损。

不同沾污铀质量对神经网络反演的结果表明，在沾污铀质量0.5 g的条件下，使用裂变产物比活度作为输入向量训练得到的神经网络，对于其他沾污铀质量条件下比活度对应包壳是否破损无预测能力。

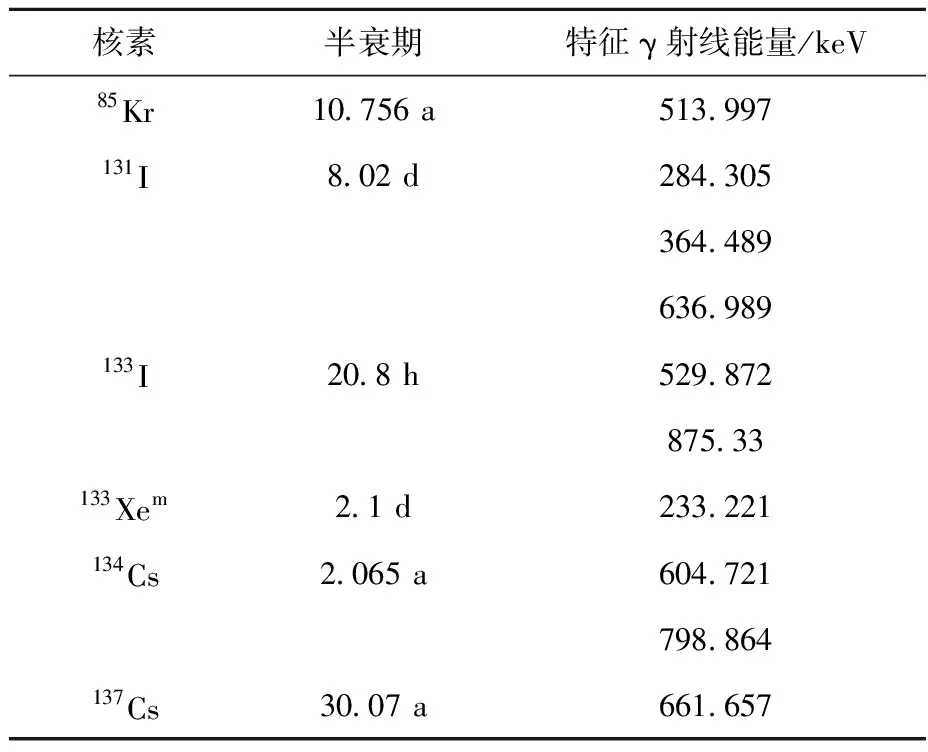
表3 进一步筛选得到的特征核素Table 3 Further selected characteristic nuclide

考虑到沾污铀对一回路裂变产物比活度的贡献与其质量呈正比，根据式(10)，使用归一化后的比活度作为输入向量，可消除沾污铀质量的影响。

(10)

仍使用沾污铀质量为0.5 g时生成的训练集，使用式(10)对比活度归一化后，再用其作为输入向量训练神经网络。测试结果表明该神经网络能准确判断不同沾污铀质量条件下对应包壳是否破损。

选取77、90、100、110、120 kW等5组单棒功率生成测试集，用训练好的神经网络分别对其进行反演，预测错误率列于表4。

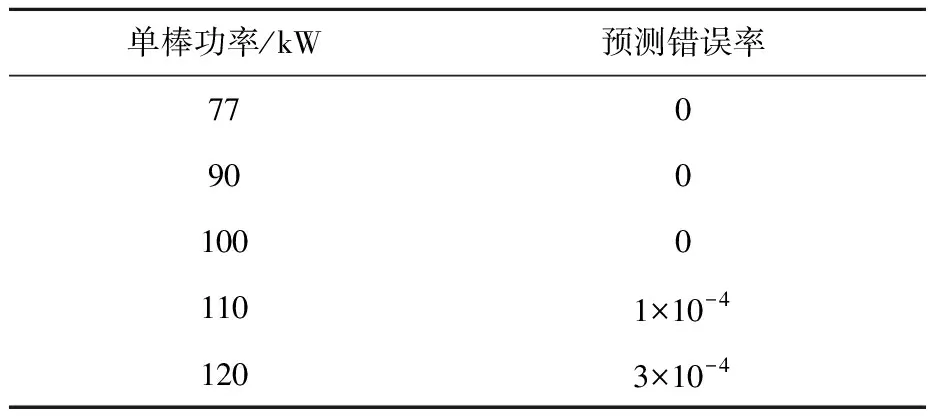
表4 不同功率下的预测结果Table 4 Prediction result at different rod powers

从表4可看出，随着功率的增大神经网络反演的误差增大，但在功率最大(120 kW)时，神经网络的反演准确率仍处在较高水平，因此在77～120 kW的范围内，功率变化对于神经网络的反演准确度影响可忽略。

3 判断包壳破损程度

3.1 训练神经网络

燃料元件的破损程度由惰性气体裂变产物的逃脱率系数来表征。基于神经网络的特点和逃脱率系数的取值范围，将破损情况分为5个等级：等级1，逃脱率系数小于1×10-7s-1；等级2，逃脱率系数处于1×10-7～1×10-6s-1之间；等级3，逃脱率系数处于1×10-6～1×10-5s-1；等级4，逃脱率系数处于1×10-5～1×10-4s-1；等级5，逃脱率系数大于1×10-4s-1。5个等级对应该神经网络输出向量的5个分量，分量的最大值将被视为判断结果。

通过设定不同的破损时间、逃脱率系数，生成192组数据作为训练集。为减少训练集数据量、提升训练效率，在启堆初期、破损初期密集采集数据，减少其他相对稳定时刻的数据采集密度。图3为神经网络训练过程中均方差的收敛情况。测试结果表明，训练好的神经网络判断包壳破损等级的正确率为99.48%。该神经网络能准确地对破损严重情况进行分级。

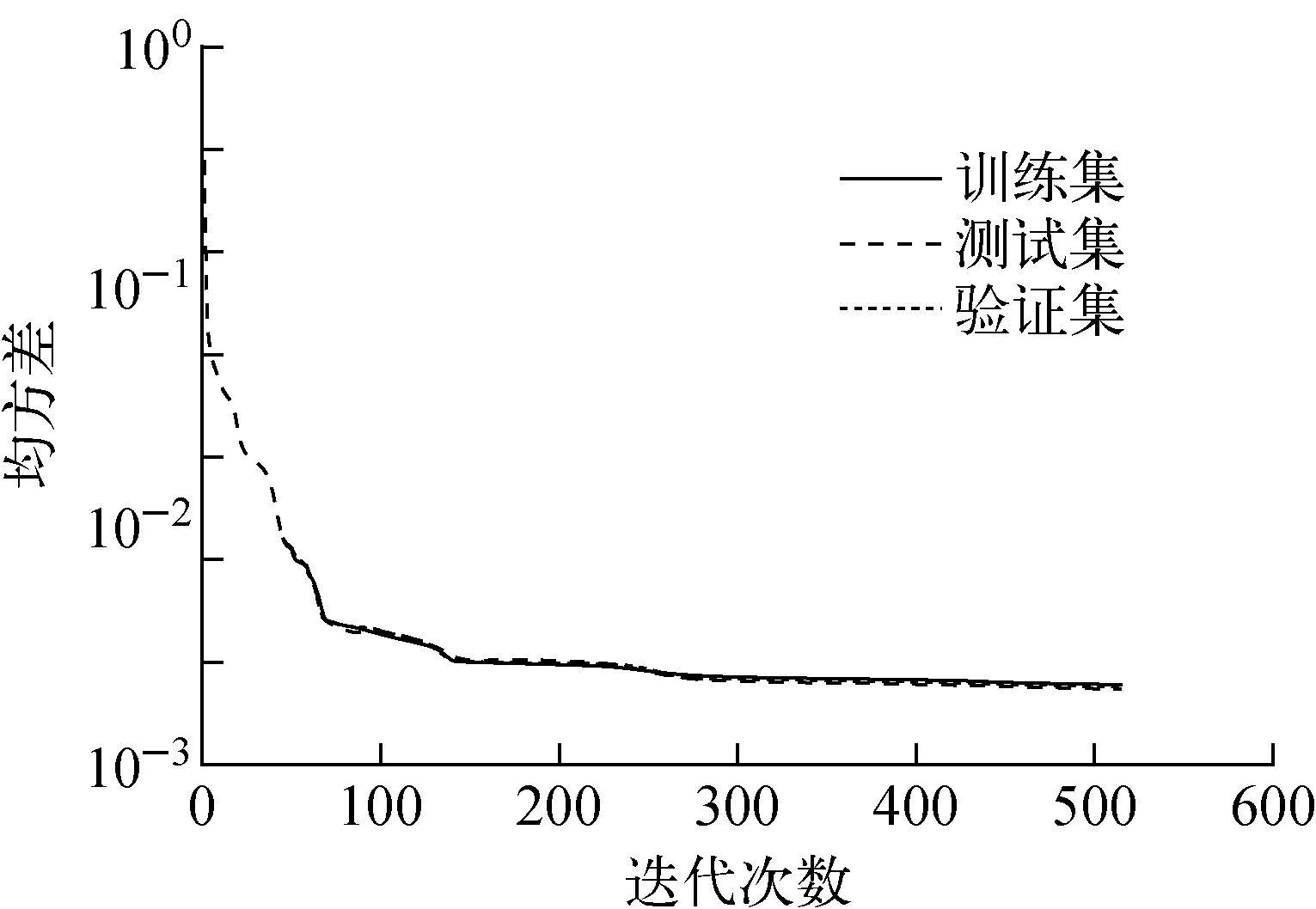
图3 包壳破损程度的神经网络均方差收敛图 Fig.3 Convergence graph of mean squared error of neural network for degree of cladding failure

3.2 敏感性分析

选取沾污铀质量不同的测试集，对该模型进行测试。表5列出对于测试集的测试结果。结果表明，用沾污铀质量为0.5 g的训练集训练得到的神经网络，在沾污铀质量不同的情况下，仍能对破损等级进行准确分级。

选取单棒功率不同的测试集，对该模型进行测试，功率范围为77～120 kW。表6列出对于测试集的测试结果。结果表明，单棒功率的变化对于判断准确率的影响较小。用单棒功率为77 kW的训练集训练得到的神经网络，在功率变化的情况下，仍能对破损等级进行准确分级。

表5 对于沾污铀质量不同的测试集的分级错误率Table 5 Error rate of classification towards test sets with different masses of tramp uranium

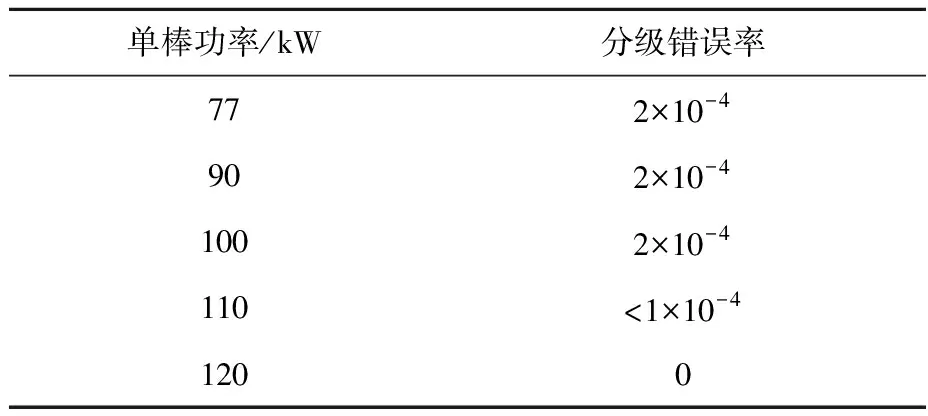
表6 对于单棒功率不同的测试集的分级错误率Table 6 Error rate of classification towards test sets with different rod powers

选取2.2节中的6种特征核素进行训练神经网络。测试结果表明，基于6种核素所训练得到的神经网络，对训练集的判断正确率为98.76%，略低于使用23种核素训练所得的神经网络的正确率99.48%，但仍表现出优越的性能。

4 与碘同位素比值法比较

碘同位素比值法是在反应堆运行经验基础上建立的判断燃料包壳破损程度的方法。

有国内学者指出：对于无燃料破损的堆芯，131I/133I的比活度比约为0.1；对于出现小破损的堆芯，131I/133I的比活度比约为1；对于出现大破损的堆芯，131I/133I的比活度比约为0.6[10]。

而美国西屋公司经验总结认为：131I/133I比活度比在0.1～0.2是开孔或大破损；在0.3～0.5是小孔眼程度的破损；大于0.5是针孔或很小的裂纹[9]。

两种判断依据最主要的区别在于131I/133I比活度比在0.1时对应的包壳破损程度。与模拟数据进行对比后发现：沾污铀质量为0时131I/133I比活度比的模拟结果与后者一致；而沾污铀质量不为0时131I/133I比活度比的模拟结果则与前者接近。故认为后者的判断依据是在未考虑沾污铀或沾污铀质量极小的情况下得到的，本研究中选择前者作为判断依据。

图4为不同沾污铀质量和不同逃脱率系数情况下，6.324×107s包壳发生破损后，所计算的131I/133I比活度比。可看出，当沾污铀质量较大但包壳破损较小时，131I/133I比活度比在0.2～0.3之间，此时比值法难以准确判断包壳的破损状态。

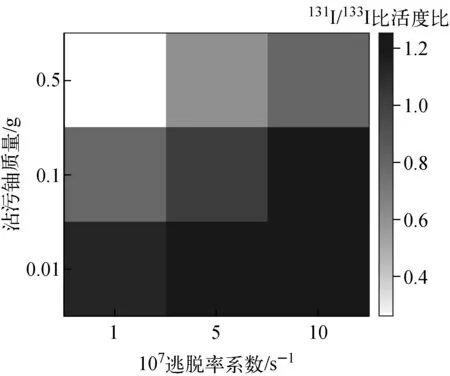
图4 碘同位素比值法结果Fig.4 Prediction result by iodine isotope ratio method

取沾污铀质量为0.5 g，破损时间为106s，逃脱率系数为10-7s-1，在破损时间较早、逃脱率系数较小的情况下，比较神经网络法与传统比值法的预测性能，如图5所示。

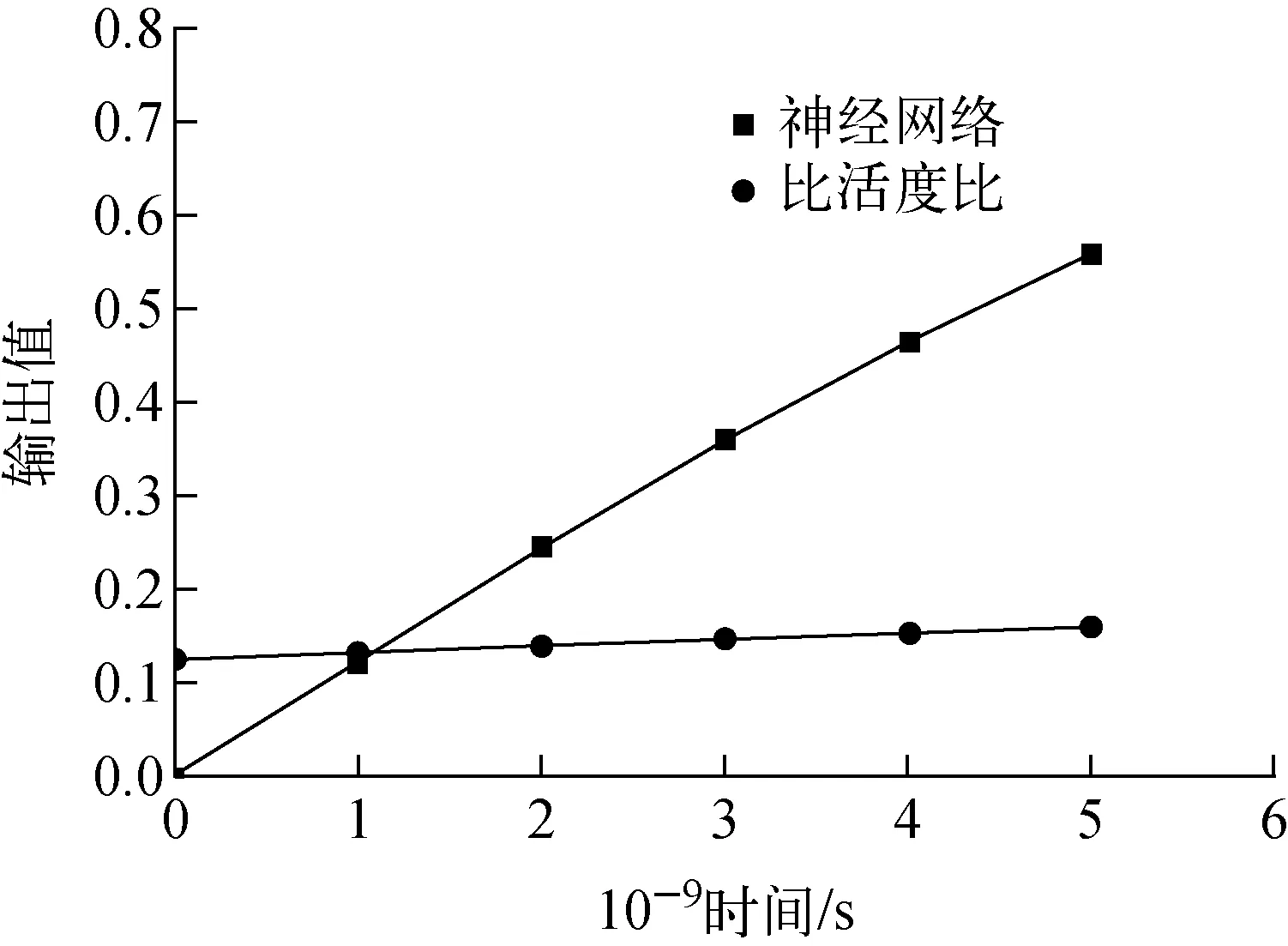
图5 发生破损后神经网络与碘同位素比活度比输出值变化Fig.5 Output of neural network and specific activity ratios of 131I and 133I after defecting

由图5可知，在上述条件下，神经网络输出的状态值上升较快，仅在5×103s后就达到了破损的判断阈值，即神经网络判断的破损时间为1.004×106s，与真实情况仅相差4×103s。与之相比，碘同位素比活度比上升较为缓慢，在1.005×106s时，比活度比仅0.159 98。经过8×104s后，该比活度比也仅上升至0.35，不能准确判断其破损状态。

在中小破口的情况下，相比于碘同位素比值法，神经网络对于包壳破损程度判断响应更快，准确度更高。

5 总结

本文基于BP神经网络，建立了通过压水堆一回路中裂变产物比活度判断燃料包壳是否破损以及破损程度的模型。通过敏感性分析，得到如下结论：

1) 用于判断包壳是否发生破损的神经网络，能在燃料棒参数发生变化的情况下，准确地判断出发生破损的时间。

2) 用于判断包壳破损等级的神经网络，能在燃料棒参数发生变化的情况下，准确地判断包壳破损的严重程度。

3) 与碘同位素比值法相比，在小破口的情况下，神经网络方法能更快、更准确地预测包壳的破损情况。

综上所述，人工神经网络可用于预测反应堆燃料包壳是否发生破损以及破损程度。