基于模糊多模型的堆芯功率控制

2020-05-07曾文杰姜庆丰谢金森

原子能科学技术 2020年3期

曾文杰，姜庆丰，谢金森，于涛,*

(1.南华大学核科学技术学院，湖南衡阳 421001；2.南华大学核燃料循环技术与装备湖南省协同创新中心，湖南衡阳 421001)

核反应堆堆芯具有非线性、参数时变性和各种扰动的不确定性等特点，基于单一功率水平处的堆芯局部模型难以准确描述扰动工况下的堆芯功率控制过程。目前，PID控制器因简单直观、容易实现，广泛用于堆芯功率控制。然而，传统PID控制器不具备参数的自适应功能，其控制参数一经取定，在堆芯功率变化过程中将不再改变，因此控制效果往往不太理想[1]。为使PID控制器达到更好的控制效果，出现了模糊PID、内模PID等多种交叉形式的PID控制方法[2-4]。

本文基于堆芯非线性模型，利用微扰理论对堆芯非线性模型进行线性化，建立堆芯传递函数模型。并基于堆芯局部模型和三角隶属度函数，建立堆芯模糊多模型，与模糊PID控制器相结合，设计堆芯功率控制系统，实现对PID控制器控制参数的在线修正。以三哩岛(Three Mile Island, TMI)型压水堆堆芯为对象，在不同初始稳态功率水平下开展堆芯功率控制的仿真及分析。

1 堆芯模糊多模型建立

1.1 堆芯非线性模型

依据核反应堆点堆建模原理，不考虑碘氙等毒物效应，建立堆芯非线性模型。该模型包括点堆动力学模型、热工水力学模型和反应性模型[5-7]：

(1)

式中：Pr为堆芯相对功率，Pr=P/P0，P0为堆芯稳态功率；cr为先驱核相对密度，cr=c/c0，c0为稳态缓发中子先驱核密度；ρ为引入堆芯的总反应性；β为缓发中子总份额；λ为缓发中子先驱核衰变常量；Λ为堆内中子代时间；ff为燃料产热总份额；Tc为冷却剂平均温度；Tf为燃料平均温度；Tin为堆芯冷却剂进口温度；μf为燃料的总热容量；μc为冷却剂的总热容量；Ω为燃料和冷却剂间的换热系数；M为质量流量热容量；αf为燃料的多普勒系数；αc为冷却剂温度反馈系数；Tf0、Tc0分别为稳态时刻堆芯燃料温度和堆芯冷却剂平均温度；ρrod为控制棒引入的反应性。

1.2 堆芯传递函数模型

利用微扰理论[8-9]对堆芯非线性模型进行线性化处理，建立堆芯状态空间模型：

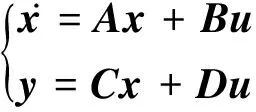
(2)

式中：u=[δρrod，δTin]T为输入量；y=[δPr, δTc]T为输出量；x=[x1,x2,x3,x4]T=[δPr,δcr,δTf,δTc]T为4×1状态变量阵；A为 4×4系统矩阵；B为4×2输入矩阵；C为 2×4输出矩阵；D为 2×2零矩阵。

A、B、C和D的表达式为：

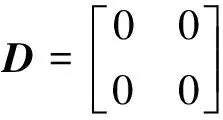
利用状态空间与传递函数转换关系式，可得到传递函数矩阵(即双输入双输出系统)的表达形式为：

(3)

1.3 堆芯模糊多模型

上述所求得的堆芯传递函数模型，在整个堆芯运行范围内，均仅在一个小的功率区间内适用，当功率发生大范围变化时，适用性低。为建立适用整个功率运行范围内的模型，选择20%FP(满功率)、40%FP、60%FP、80%FP、100%FP等5个功率水平下的线性模型GP1、GP2、GP3、GP4、GP5建立堆芯局部模型。利用三角形隶属度函数求取在整个功率水平范围内的堆芯模糊多模型。在整个功率水平范围内的堆芯模糊多模型隶属度函数如图1所示[10]。图1中，第i条规则的描述为：Zi：ifPrisMithenyoi=GPi(i=1,…,5)。式中：Zi为第i条模糊规则；M1、M2、M3、M4和M5分别为功率水平20%FP、40%FP、60%FP、80%FP和100%FP处的模糊集；GPi为对应于模糊集Mi的线性模型。μMi(Pr)为Pr隶属于Mi时的隶属度，权重qi为：

(4)

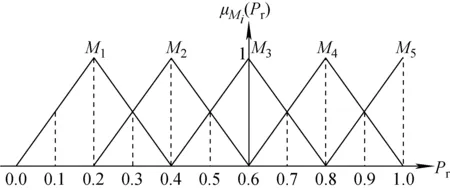
图1 三角隶属度函数Fig.1 Trigonometric membership function

因此，在整个功率水平范围内的堆芯模糊多模型表达式为：

(5)

2 堆芯功率控制

2.1 堆芯功率控制系统设计

1.2节中堆芯传递函数模型是双输入双输出的，虽然控制棒反应性和堆芯进口温度均是堆芯的输入量，但仅前者(即控制棒的反应性)为可控量，堆芯的进口温度不可控[11]。通过控制堆芯功率可实现对堆芯冷却剂平均温度的控制。因此可单独采用堆芯功率反馈控制，如图2所示。

2.2 堆芯功率控制系统开发

以TMI型压水堆堆芯为对象，其堆芯结构参数列于表1[5-6]。

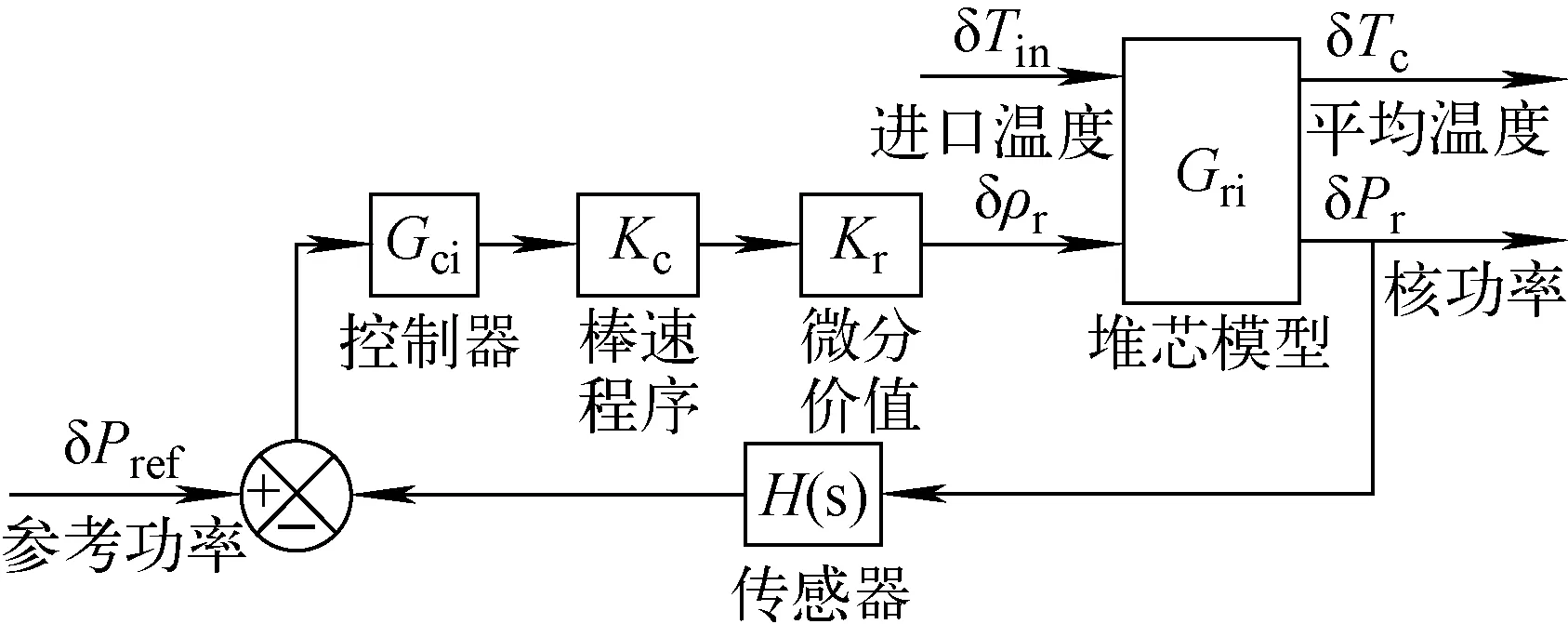
图2 基于核功率反馈控制的棒控系统Fig.2 Rod control system based on nuclear power feedback control

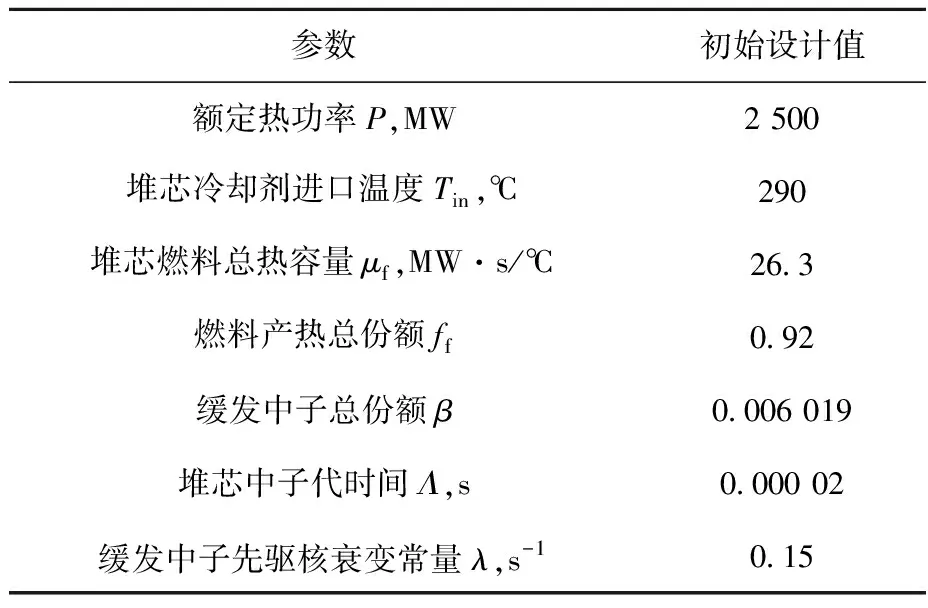
参数初始设计值额定热功率P,MW2 500堆芯冷却剂进口温度Tin,℃290堆芯燃料总热容量μf,MW·s/℃26.3燃料产热总份额ff0.92缓发中子总份额β0.006 019堆芯中子代时间Λ,s0.000 02缓发中子先驱核衰变常量λ,s-10.15

考虑到方程组中，参数Pr0随着功率的变化而改变。当功率变化时，参数αf、αc、μf、μc、Ω与M均会随着堆内温度的变化而改变[5-6]。

(6)

(7)

M(Pr)=(28.0Pr+74.0)×106

(8)

αf(Pr)=Pr-4.24

(9)

αc(Pr)=-4.0Pr-17.3

(10)

通过将20%FP、40%FP、60%FP、80%FP、100%FP等5个不同堆芯功率水平处的传递函数模型以及对应功率下所设计的控制器进行三角隶属度加权整合，基于MATLAB/Simulink[12]开发堆芯功率控制系统，如图3所示。仿真系统通过设计参考功率、模糊PID控制器，实现了堆芯实际功率与参考功率的对比输出。

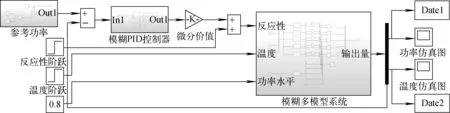
图3 基于模糊多模型的堆芯功率控制系统仿真框图Fig.3 Simulation block diagram of core power control system based on fuzzy multi-model

3 仿真结果及分析

在80%FP、100%FP两个初始稳态功率水平下，模拟在50 s以前，系统按初始稳态功率运行。在50 s时，堆芯功率水平阶跃下降10%FP并稳定运行60 s后阶跃恢复至原功率水平，仿真结果如图4所示。从图4可见，在不同初始功率水平下，堆芯功率发生10%FP的阶跃变化时，系统在模糊PID控制下可迅速做出反应，减小实际功率与参考功率之间的误差，此过程所消耗的时间较短。从温度变化图中可知，堆芯冷却剂平均温度偏差与堆芯相对功率同步变化，变化趋势相同，最大冷却剂平均温度偏差均为-1.3 ℃。

在30%FP初始稳态功率水平下，模拟在50 s以前，系统按初始稳态功率运行。在50 s时，目标负荷以5%FP/min的速率线性上升20%FP，然后，稳定运行210 s后，以5%FP/min 的速率线性下降至稳态初始功率，仿真结果如图5所示。从图5可知，对系统进行堆芯功率追踪时，堆芯功率的运行参考值与堆芯功率模糊PID控制值相接近，未出现大的偏差。堆芯冷却剂平均温度偏差的变化与堆芯相对功率的变化同步。由此可见，模糊PID控制器可实现对堆芯功率的良好跟踪。

a——80%FP-70%FP-80%FP功率变化；b——100%FP-90%FP-100%FP功率变化图4 80%FP、100%FP堆芯功率水平下相对参考功率阶跃变化10%FP仿真结果Fig.4 Simulation result of relative reference power step change of 10%FP at 80%FP and 100%FP core power level

图5 30%FP稳态初始功率水平下的功率跟踪响应Fig.5 Power tracking response at steady-state initial power level of 30%FP

在100%FP初始稳态功率水平下，模拟在300 s以前，系统按初始稳态功率运行。在300 s时，目标负荷以15%FP/min的速率线性下降75%FP。然后，稳定运行。仿真结果如图6所示。从图6可知，即使加大功率线性变化速度，堆芯功率的运行参考值依旧与堆芯功率模糊PID控制值相接近，且堆芯冷却剂平均温度偏差与相对功率同步。由此可见，采用模糊PID进行不同初始稳态功率下的局部控制是可行的。

在100%FP功率水平下，引入堆芯冷却剂进口温度阶跃2、5 ℃扰动时，得到如图7所示的响应曲线。在10 s时刻，引入堆芯冷却剂进口温度阶跃扰动时，相对功率迅速下降，在模糊PID控制器作用下，堆芯相对功率缓慢上升，最后趋于稳定。从温度变化图中可知，温度变化趋势渐渐减小，最后趋于稳定。并且稳定值与引入堆芯冷却剂进口温度阶跃值相近。这是由于经过一段时间后，系统产生的反应性反馈抵消引入堆芯进口温度阶跃扰动对功率的影响，堆芯功率水平最终回到初始稳态水平，系统达到能量平衡。此时，堆芯冷却剂出口温度与堆芯冷却剂进口温度的变化相同。

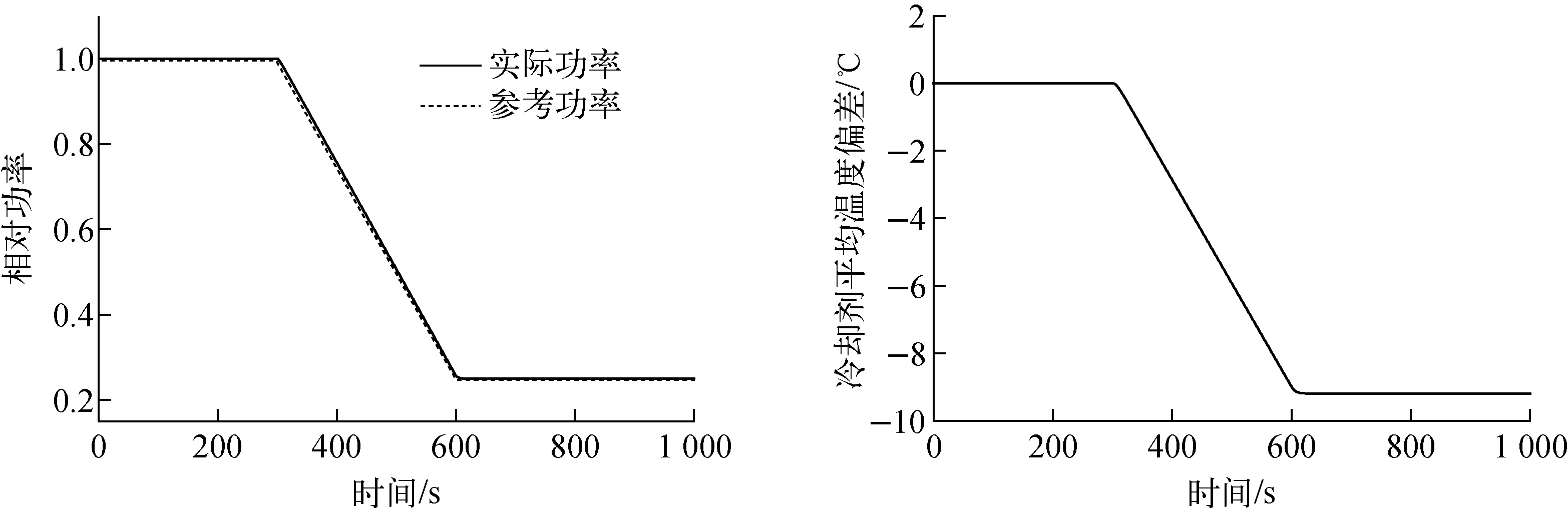
图6 100%FP稳态初始功率水平下的功率跟踪响应Fig.6 Power tracking response at steady-state initial power level of 100%FP

a——2 ℃堆芯进口温度阶跃扰动；b——5 ℃堆芯进口温度阶跃扰动图7 100%FP稳态初始功率下的堆芯进口温度扰动响应Fig.7 Response of core inlet temperature perturbation at steady-state initial power of 100%FP