堆内辐照氚增殖剂球床有效热导率分析

骆贝贝，王玉林，葛艳艳，占 勤，杨洪广

(中国原子能科学研究院 反应堆工程技术研究部，北京 102413)

在氘-氚反应的聚变反应堆中需不断地为聚变反应提供氚核素，是聚变反应堆商业化的关键技术，为此在聚变反应堆的外围设计可产生氚核素的固体包层，即固态氚增殖剂包层[1]。作为固态增殖剂包层的推荐材料，正硅酸锂(Li4SiO4)产氚能力较强，具有良好的机械性能和抗辐照性能。其中由Li4SiO4小球堆积形成的球床形式的包层是我国聚变反应堆重点研究的固态氚增殖剂包层形式之一[2-3]。在运行中，氚增殖剂球床在堆内辐照时处于高温环境[4]，由于球床内由Li4SiO4小球堆积形成的特殊离散结构形式，球床内的传热行为十分复杂，需综合考虑气体和固体的导热、小球间的接触导热及辐射换热等因素。一般用随温度变化的有效热导率来表征球床的导热能力。国内外已开展了相关的堆外实验研究，一般采用稳态热流法[5]或瞬态热线法[6]对外加热源的氚增殖剂球床进行有效热导率的测量。在中国先进研究堆(CARR)上首次开展的氚增殖剂球床组件辐照实验，完成了在堆内辐照情况下球床有效热导率的测量[7]。本文结合堆内辐照实验中不同反应堆功率下球床内的温度分布和中子物理计算所得的球床发热功率，反推计算得到Li4SiO4球床的有效热导率，并将该结果与有关球床内有效热导率理论计算结果及实验结果进行对比分析。

1 辐照实验组件结构

在CARR开展氚增殖剂球床组件辐照实验时，综合考虑辐照处的中子通量密度及孔道的实际使用情况，选择内径为φ70 mm的垂直孔道开展相应实验研究，该孔道与堆水池联通，内部无强迫冷却，依靠孔道外部的重水箱为辐照组件提供冷却。在孔道内架设辐照工艺管，将辐照组件与孔道内的水隔离。图1为球床组件在垂直孔道中的横截面示意图。

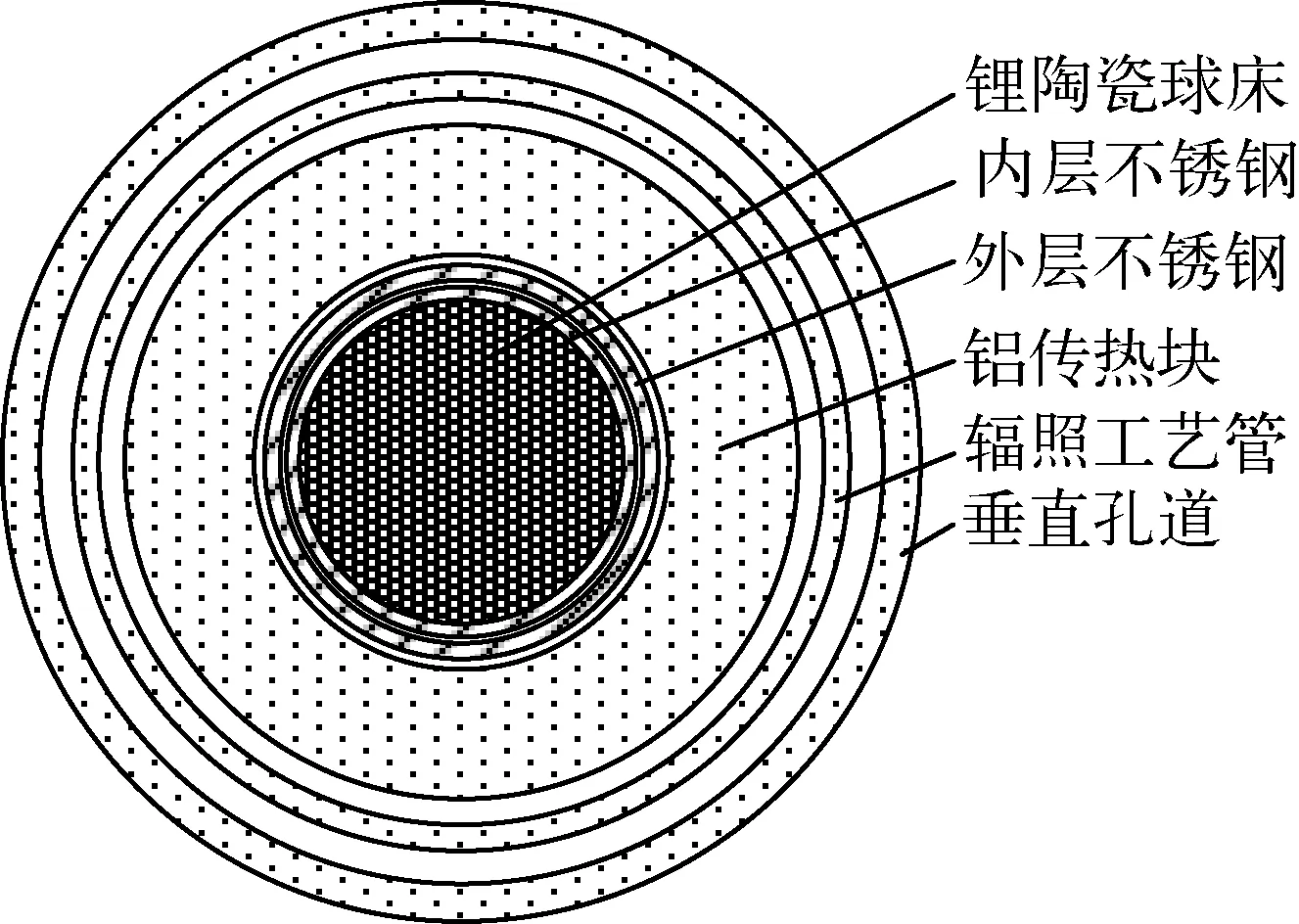
图1 球床组件横截面示意图Fig.1 Schematic of cross section for pebble bed assembly

实验中使用的球床由Li4SiO4陶瓷小球(6Li的富集度为7.5%)在不锈钢容器中堆积形成。Li4SiO4陶瓷小球采用湿法制备，经筛分选择球径为0.95～1.0 mm的小球，小球的真实密度为2.29 g/cm3。球床的高度为120 mm，直径为33.2 mm，堆积系数为56%。球床的不锈钢外壳即内层不锈钢外另设1层不锈钢，两层不锈钢间为渗透气隙，其中的气体成分与球床中的吹扫气体一致，均为氦气。由于球床在堆内辐照的过程中发热量较大，为保证组件安全，利用金属铝具有较好的导热特性，在球床外部设置铝传热块，长度为650 mm。外层不锈钢与铝传热块间、铝传热块与辐照工艺管间为调温气隙，根据实验要求可选取氦气或氩气等作为调温气体。球床组件中的气体间隙均与单独的气体回路连接，以实现在线氚提取、氚渗透测量及辐照温度调节功能。根据孔道内中子通量密度分布及前期大量物理-热工验证计算确定了球床组件在CARR垂直孔道的位置[8]，为得到最佳的辐照实验结果，将球床的底部放置于堆内标高为+1.3 m的位置，铝传热块的底部放置于堆内标高+1.2 m的位置(堆芯中心标高为+1.2 m)。图2示出由MCNP计算所得的反应堆功率为20 MW时球床和铝传热块高度方向上平均中子通量密度分布。图中坐标0 cm对应堆内标高+1.2 m。由图2可知，由于锂陶瓷球床为中子的强吸收体，球床与其对应的铝传热块高度上的中子通量密度的分布均呈现中间低、两边高的趋势。

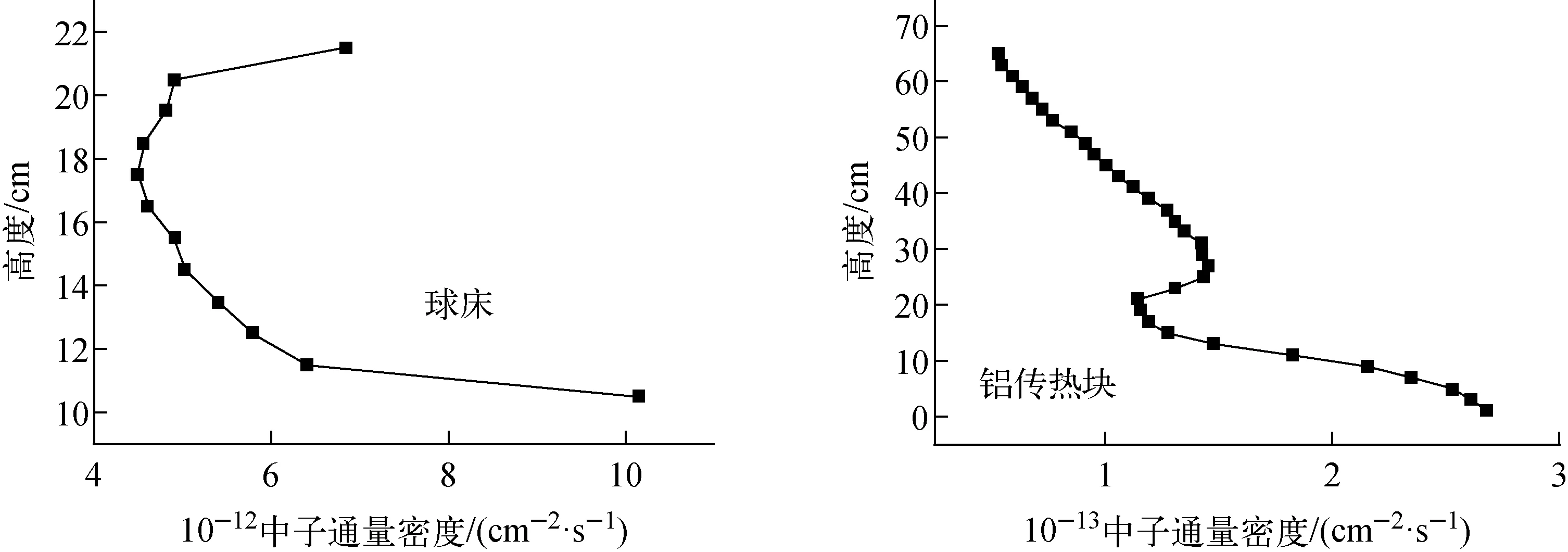
图2 球床和铝传热块高度方向上平均中子通量密度分布Fig.2 Average neutron flux density distribution for different heights of pebble bed and aluminum heat transfer block

为实现球床内测温热电偶的准确定位，在堆积球床的上方设置热电偶的定位孔。在球床高度的中心位置，分3个角度(0°、120°和240°)的扇面安装3组，每组5只K型热电偶，热电偶均匀分布在球床的半径方向上，用于测量在不同反应堆功率下的球床温度分布。在不同扇面上同一半径处测得的温度可减少后续有效热导率求解时的误差。图3为球床组件的结构示意图。

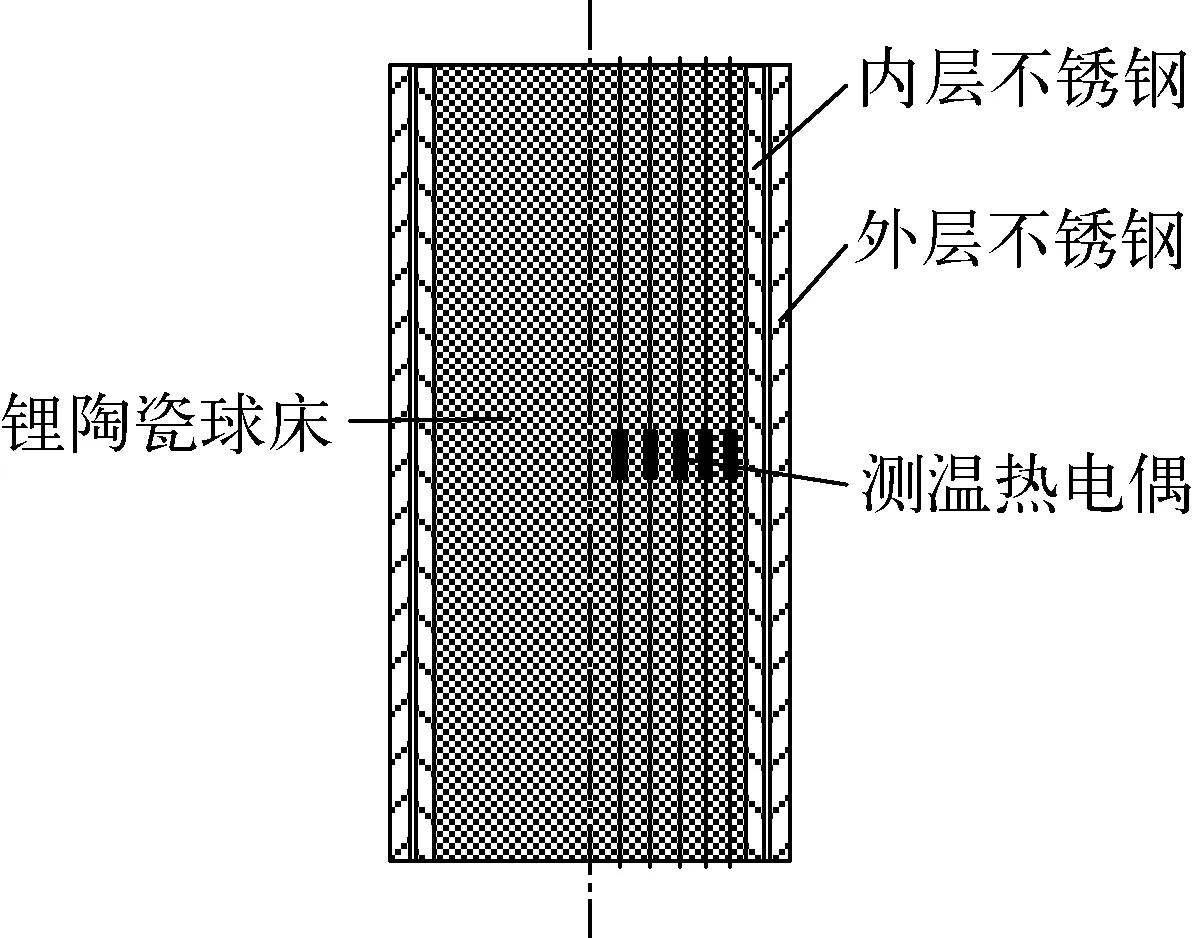
图3 球床组件结构示意图Fig.3 Structure schematic of pebble bed assembly

实验中通入球床内的吹扫气体压力约为100 kPa，流量为200 mL/min。吹扫气体的流速非常低，可近似认为球床内的气体为滞止状态。实验中采用反应堆加热及改变调温气体成分的方式调节球床内温度。根据CARR运行情况以及材料辐照安全的要求，在反应堆运行条件下要求球床内温度不得高于850 ℃。

2 辐照实验过程

为确保反应堆安全及辐照组件的完整性，并获得不同温度下球床的有效热导率数据，进行两轮升功率-降功率实验，第1轮实验中使用导热性能较好的氦气作为调温气体，球床的温度较低；第2轮实验中使用氩气，球床的温度较高，实验中需关注高功率时温度是否超过辐照球床的最高限制温度850 ℃。实验的主要步骤如下：

1) 实验开始前完成辐照装置的抽真空操作，并按照实验要求对各间隙进行载气配置，辐照组件中的球床吹扫气体为氦气，调温气体为氦气，监测压力、流量、湿度等参数，保证其满足有效热导率测量实验的要求；

2) 启动反应堆，按照0.5、5、10、20和30 MW的台阶提升功率。在反应堆达到目标功率后记录各测点温度，每个功率台阶稳定15～30 min，直至各测点的温度趋于稳定，记录稳定后的球床温度分布等参数；

3) 依上述功率台阶下降反应堆功率，记录每个功率台阶稳定后相应的实验参数；

4) 根据第1轮实验测量数据，调整调温气隙内的成分为氩气，重复反应堆升功率-降功率过程，记录实验数据。

3 实验结果及数据处理

图4示出采用氩气为调温气体时球床内各测点在不同反应堆功率下达到稳定时的温度测量值。由实验结果可知，在反应堆功率为30 MW时球床内最高温度在辐照安全限值850 ℃以下，堆功率越高，不同方向同一半径处的温度测点间的测量值差别越大。

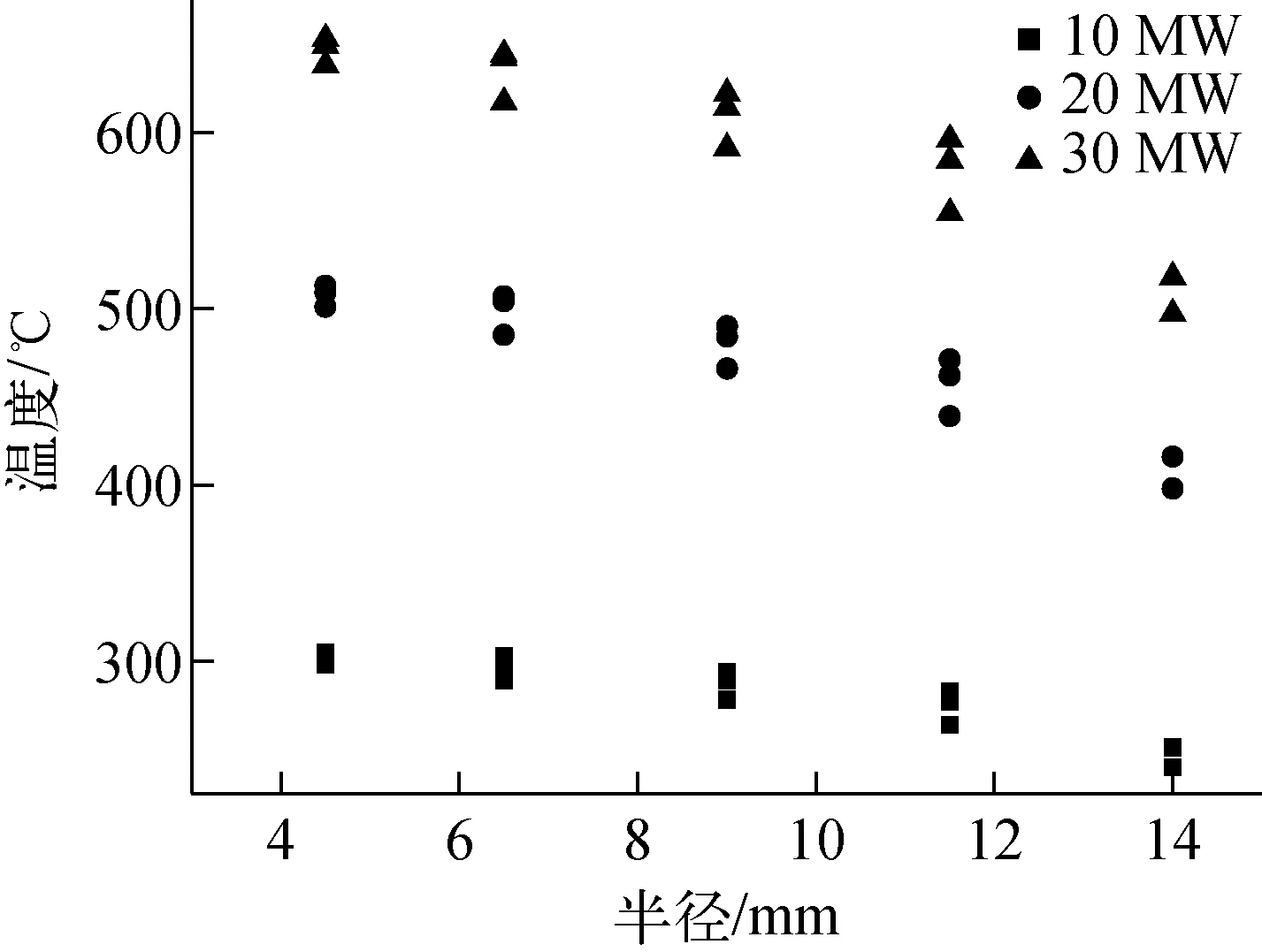
图4 不同反应堆功率下球床内温度测量值Fig.4 Measurement value of temperature in pebble bed under different reactor powers

在堆外球床有效热导率测量的稳态热流法实验中，外加热源的功率一般较低，以保证在球床内产生较小的温度梯度，可近似认为该温度区间内的有效热导率为一定值。而堆内辐照情况与堆外实验用外加热源不同，球床的导热过程为含内热源的导热，球床内的发热功率很高，温度梯度较大，且无法通过直接测量得到球床的发热量，需结合中子物理计算得到的球床发热功率进行有效热导率的反推。

计算球床内有效热导率使用的公式为含有内热源的圆筒导热公式：

(1)

式中：r1、r2分别为对应圆筒的内半径和外半径，m；T1、T2为对应于内半径和外半径位置上的温度，K；Qin为圆筒内部包容物的发热功率，W；λ为热导率，W/(m·K)。

图5为根据MCNP计算得出的反应堆功率为20 MW时，球床中心高度处以球床中心为坐标原点0 mm向外的球床径向发热功率分布，由图5可看出，由于球床外Li4SiO4小球对中子的吸收，使球床内部中子通量密度降低，即中子的自屏效应，这样就使球床中心部分的发热功率远低于外边界部分的。计算时假设球床的发热总功率与反应堆功率呈正比。

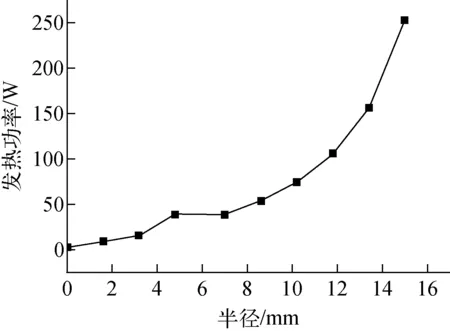
图5 球床径向发热功率分布Fig.5 Radial heating power of pebble bed

计算中根据球床中热电偶的位置对球床径向进行节点划分。由球床在径向上的发热功率分布以及不同反应堆功率下球床的温度测量数据，计算得到每两个相邻热电偶之间平均温度对应的有效热导率，在去除误差较大的计算值后对有效热导率的结果进行线性拟合。

图6为球床有效热导率的实验值及其线性拟合。由线性拟合得到的堆内辐照环境下锂陶瓷球床有效热导率随温度的变化的计算公式为：

λeff=0.758+4.074×10-4tm

(2)

式中：λeff为球床的有效热导率，W/(m·K)；tm为球床温度，℃。

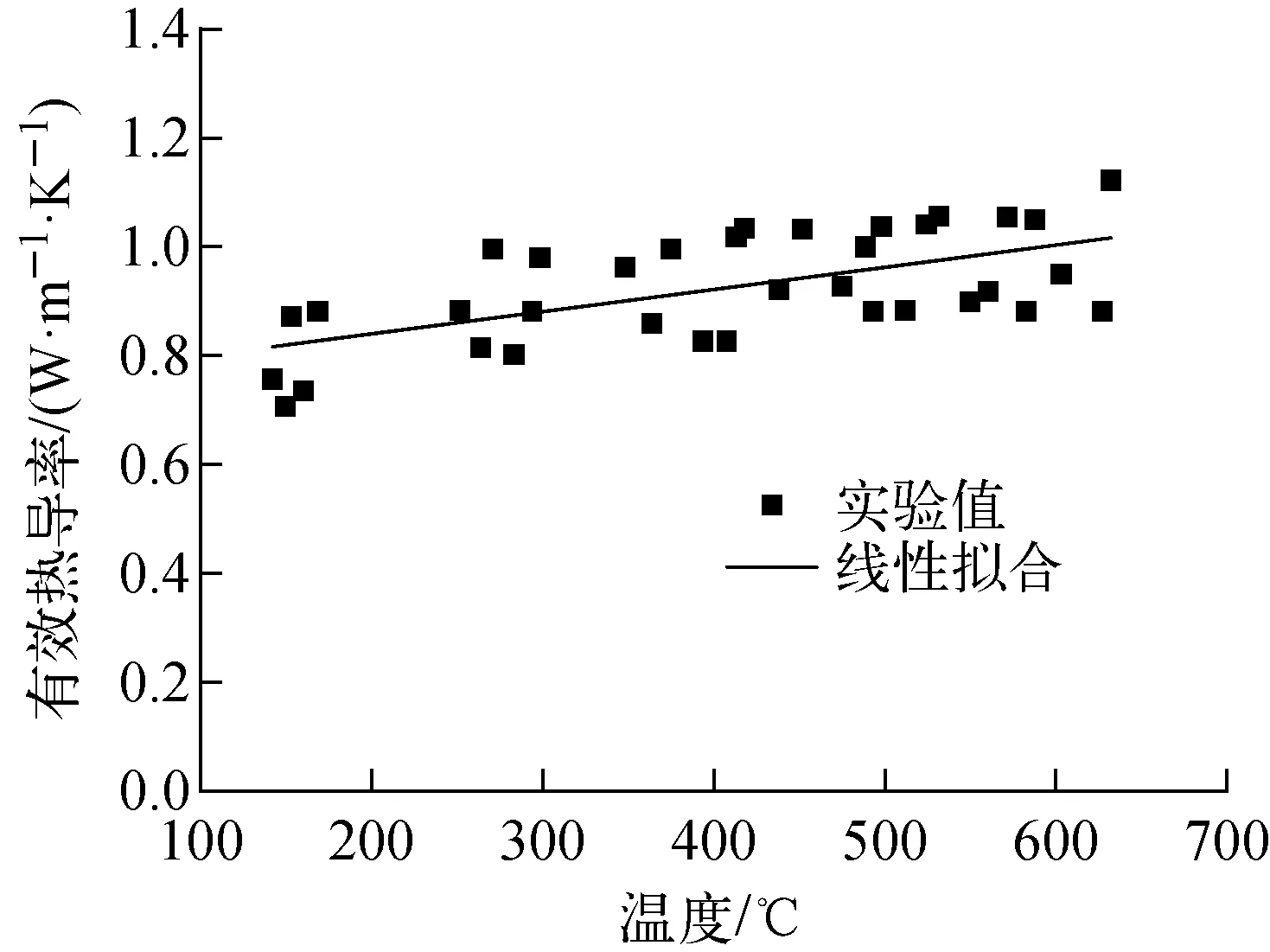
图6 球床有效热导率的实验值及其线性拟合Fig.6 Results of experiment and linear fitting of effective thermal conductivity in pebble bed

由图6可看出，实验值较为分散，实验值与线性拟合的最大偏差为11.6%左右。分析其原因可能是在计算中采用了按周向均匀分布的球床径向释热率计算结果，而在实际堆内辐照过程中由于在球床面对堆芯方向和背对堆芯的方向存在中子注量率“阴阳面”的问题，球床径向不同方向的发热功率分布并不相同。因此在不同径向方向同一半径处的体积释热率是相同的这一假设是较为粗糙的。

图7示出采用C语言编写的含内热源圆柱的一维温度分布计算程序使用上述锂陶瓷球床有效热导率公式计算得出的球床内温度分布与实验值的对比。由实验值及由有效热导率计算得到的球床径向温度分布可知，二者符合较好，最大相对偏差为6.7%，验证了球床有效热导率计算值的准确性。

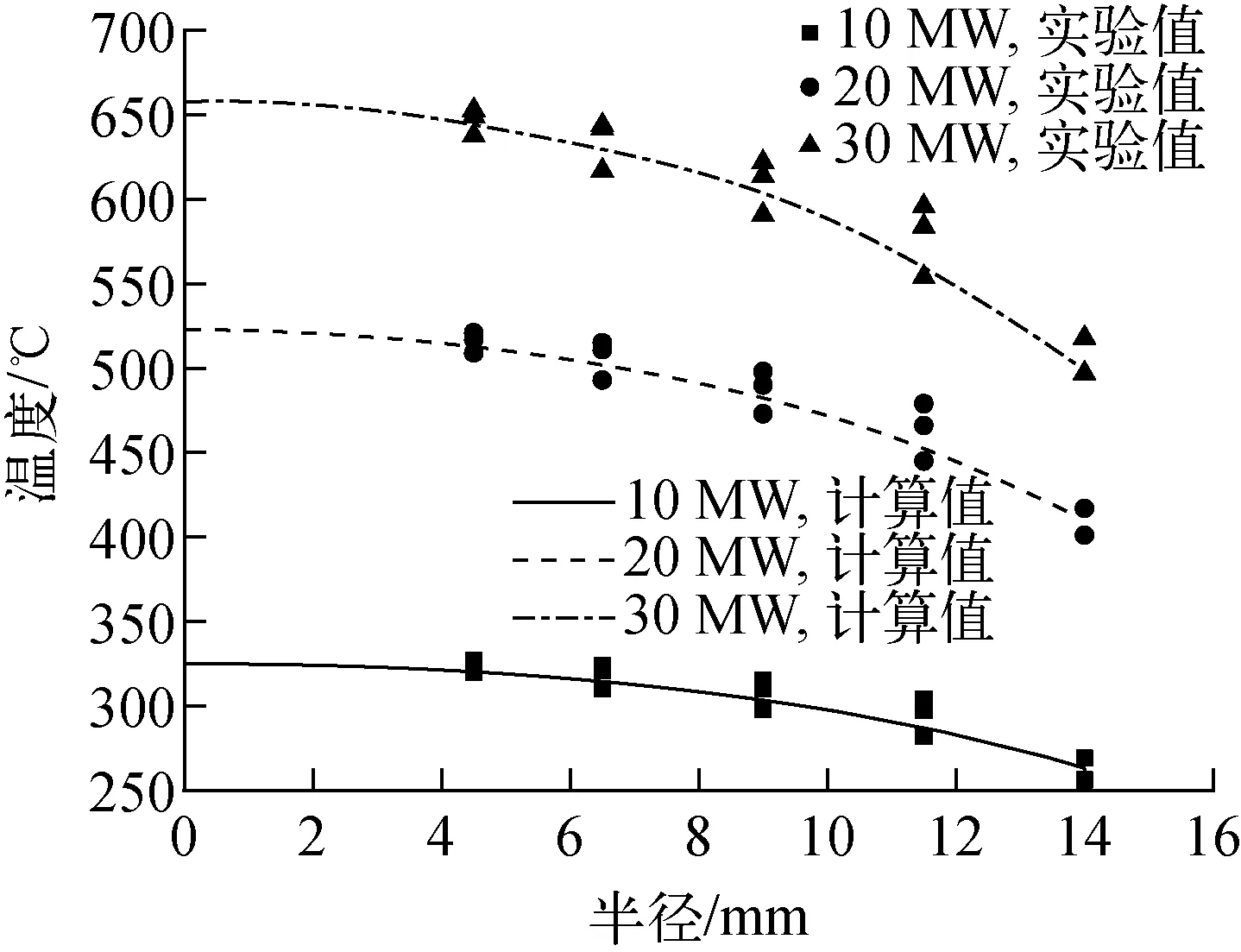
图7 不同堆功率下球床内温度实验值与一维程序计算值比较Fig.7 Comparison of experiment value of temperature and result of 1D code calculation in pebble bed under different reactor powers

4 球床有效热导率的理论模型

在工程上已有较为成熟的应用于球床有效热导率计算的公式[9]。理论分析中将球床中的热量传递分为3种方式，即通过气体和固体的导热、辐射换热及通过小球间接触面的导热。根据这3种传热机理，将有效热导率分为3个部分：

(3)

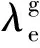
(4)

式中，κ为固相热导率λs与气相热导率λf的比值，即：

κ=λs/λf

(5)

参数B与球床孔隙率ε有关：

(6)

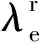
(7)

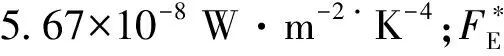
(8)

Λ=λs/4dpσT3

(9)

式中，dp为球床中小球的直径，m。

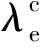
(10)

(11)

(12)

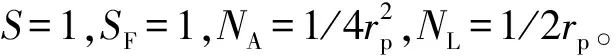
通过计算以上3种不同传热机理导致的有效热导率之和即为考虑接触面传热的改进型ZBS模型。根据Donne等[13]对Li4SiO4物性参数的研究，计算中取锂陶瓷的热导率为：

λs=(1.98+850/T)(1-p0)/

[1+p0(1.95-8×10-4T)]

(13)

式中，p0为锂陶瓷小球中的孔隙率。

吹扫气体氦气的热导率[14]为：

λf=0.39×10-2T0.645

(14)

5 结果与讨论

Donne等[5]采用稳态热流法测量了吹扫气体为氦气、小球直径为0.25～0.63 mm、堆积系数为65%的Li4SiO4球床的有效热导率。由实验测得气体压力在100～300 kPa范围内球床的有效热导率与平均温度的关系为：

λeff=0.768+4.96×10-4tm

(15)

Liu等[15]测量了氦气压力为100 kPa、小球直径约为1 mm、堆积系数为59.7%的Li4SiO4球床的有效热导率，并将其实验结果进行了线性拟合，得出球床有效热导率随平均温度的变化规律为：

λeff=0.753+5.17×10-4tm

(16)

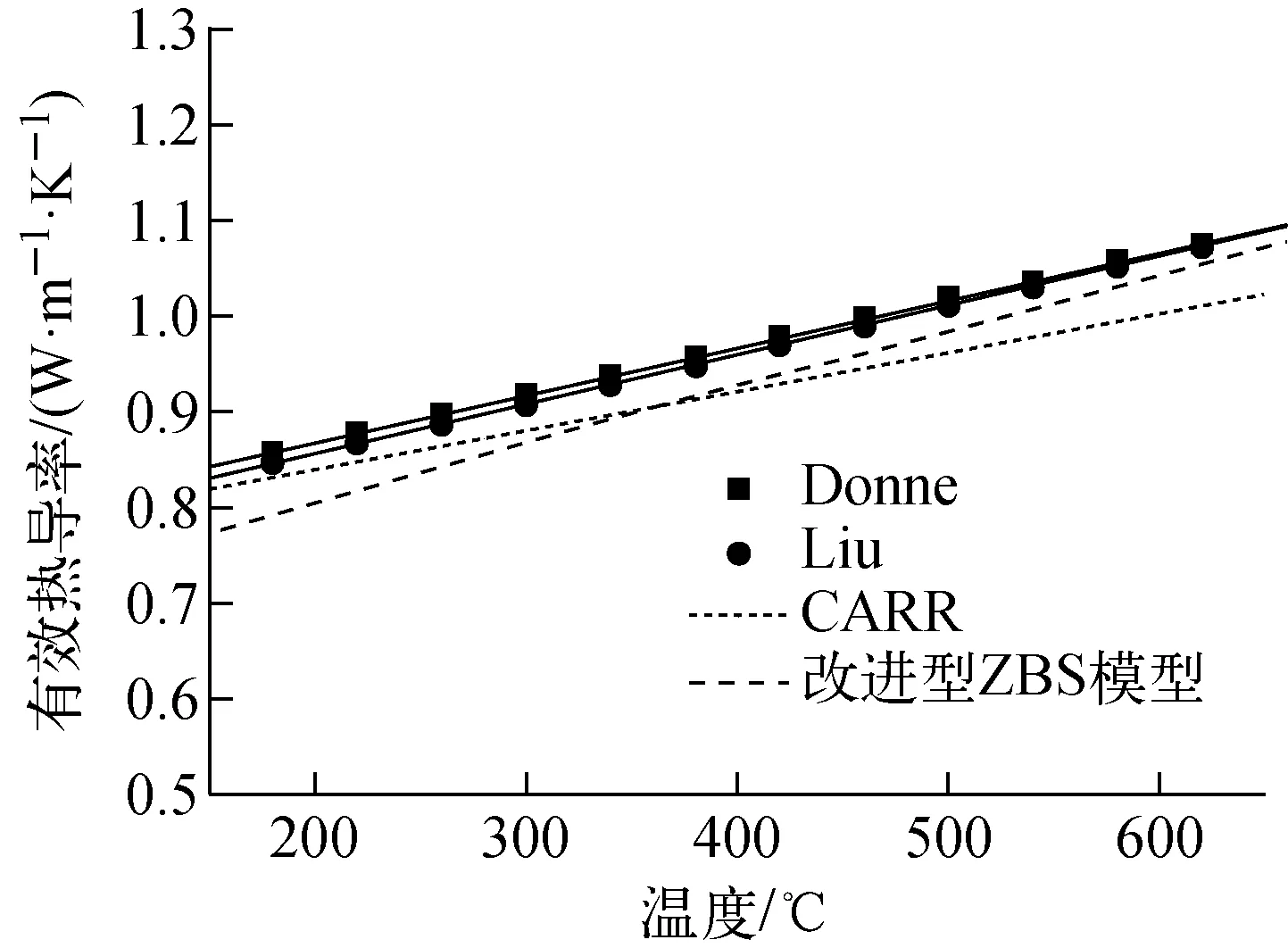
图8 Li4SiO4球床有效热导率的理论值与实验值比较Fig.8 Comparison of theoretical and experimental results of Li4SiO4 pebble bed

图8为由改进型ZBS模型(堆积系数为60%)计算、Donne等的实验、Liu等的实验以及CARR内辐照实验测得的Li4SiO4球床的有效热导率的对比。可看出，在堆内辐照实验测量的温度区间(150～650 ℃)，实验值与理论值差别较小，且球床的有效热导率随温度有着相同的变化趋势。由图8可看出，CARR内辐照实验测得的球床有效热导率实验值略小于堆外实验值，与改进型ZBS模型计算所得的理论值也存在偏差，在温度为650 ℃时二者的相对偏差约为4.5%，分析其原因如下：1) 球床的有效热导率受堆积系数的影响较大，而堆外实验所使用的球床堆积系数均大于堆内实验所使用的；2) 各实验中Li4SiO4陶瓷小球的制造存在差别，必然会导致小球本身的热导率的不同，进而影响球床的有效热导率；3) 在辐照过程中陶瓷小球的性状可能发生改变，辐照肿胀及小球的破裂等均会影响球床的有效热导率，而在改进型ZBS模型中未考虑该效应，应借助辐照后检验技术对球床进行进一步检查。

6 结论

本研究根据在CARR内辐照时氚增殖剂球床在不同功率下的温度分布结果，结合MCNP计算得出的球床发热功率进行了球床有效热导率随温度变化的计算公式的求解。根据一维程序计算得出的球床内温度分布与堆内实测温度的对比，实验所得的球床有效热导率和与改进型ZBS模型、堆外实验结果的对比分析，可得出以下结论。

1) 由一维导热程序得出的球床内温度分布的计算值与堆内辐照实验测得的温度分布较好吻合，证明采用不同温度测点间的平均温度以及MCNP计算所得的热量反推得出球床有效热导率这一方法的合理性。

2) 根据堆内实验得出的Li4SiO4球床的有效热导率符合堆外实验以及改进型ZBS模型计算得出的理论值的变化趋势，在实验的温度范围内，堆内实验得出的球床有效热导率略低于堆外实验值，可能是由于堆内实验中球床堆积系数较低造成的；实验值与理论值存在一定的偏差，可能是由于高温辐照环境下球床内小球的性状发生了改变，在后续研究中需结合辐照后检验技术进行证实和分析。