微生物燃料电池数学模型的研究进展

米广宇，尹 立，吕洪凤*

(1.中国农业大学烟台研究院，山东 烟台 264670；2.中国农业大学理学院，北京 100083)

能源危机、环境污染正在严重危害着人类的生活。微生物燃料电池(MFC)可以借助微生物的催化作用直接将有机酸、糖类等有机物的化学能转化为电能，且同时实现对污染物的处理，具有原料来源广泛、操作条件温和、生物相容性好等优点，近年来已成为清洁高效发电装置研究的热点之一。MFC的研究主要集中于产电厌氧细菌、电极材料、电池反应器构型、电子受体类型等方面，在废水处理、重金属回收、生物修复等领域具有广阔的应用前景。如，MFC可以利用海底淤泥中的有机物和微生物，在海底为无人值守产电装置产电；也可以利用少部分血糖为超微型心脏起搏器供电[1]。

目前对MFC的研究大多处于实验阶段，系统内部的各种生化反应及相关参数对MFC产电效率的影响仍不是很清楚。实验研究各参数或参数间组合对MFC的影响既费时又费力，且未必有理想的效果；而在仿真环境下，数学模型可以相对容易地修改参数，也可以解决低容量和反应堆不稳定等问题[2-4]。虽然MFC数学模型的发展正渐趋成熟，但仍存在一些不足，如描述阳极侧生物膜内物质、能量、电荷关系的研究仍需改进[5]。根据反应所需极室个数，将数学模型分为两大类：单室模型和双室模型。作者介绍了MFC数学模型的近期研究概况，论述了MFC数学模型的几种代表性单室模型和双室模型的研究进展。

1 MFC数学模型简介

MFC是一个动态变化装置，其工作过程由代谢物和细菌介质间的生化过程、电极间氧化还原反应的电化学过程和物质运输过程三部分组成。MFC数学模型的建立需从生化动力学、电化学、物质平衡三方面入手，分别结合Monod方程、Nernst方程、Butler-Volmer方程等进行详细的表达。相应地，模型有稳态/动态、单物种/多物种、一维/多维等多种组合方式。

根据产电机制不同，MFC可分为单极室MFC和双极室MFC。单极室MFC阴极暴露在空气中，无阴极室物质，在单室阳极处被微生物氧化，电子从阳极经由外电路到达阴极，氧气作为直接的电子受体，质子转移到阴极并经过质子交换膜到达阴极。双极室MFC由质子交换膜连通的厌氧室和好氧室组成，阴极、阳极的外部通过导线连接构成循环电路。在厌氧室，物质被微生物氧化，电子被外加载体或者介体转移到阳极，或直接通过微生物呼吸酶转移到阳极；在好氧室,电子通过外电路、质子通过质子交换膜分别到达阴极化合形成水[6]。

根据MFC的分类标准，将MFC数学模型分为以阳极侧为基础的MFC单室模型和包括厌氧室、好氧室两个电极室的MFC双室模型，各MFC数学模型的表达式见表1。

2 以阳极侧为基础的MFC单室模型

传统的以空气作为阴极的单室MFC，省略了阴极，由空气中的氧气作为电子的最终受体。以阳极侧为基础的MFC单室模型建立在阳极，假设所有阳极产生的电子和质子全部消耗在阴极进行氧化还原反应。经典MFC单室模型见图1。

2.1 一维稳态单物种模型

1995年，Zhang等[7]利用Monod方程、Nernst方程、Tafel方程构建了第一个一维单物种模型，用介质2-羟基-1,4-萘醌来传输电子。通过模拟，他们发现电流的输出量主要取决于底物浓度和介质浓度，MFC电流输出量与遵循法拉第电解定律的化学反应有关。该模型还预测了底物电流输出和介质浓度等其它变量之间的关系。该模型的优点在于，充分考虑了代谢物和介质间的一级反应，并建立起输出功率和外部介质浓度之间的关系；不足在于，忽视了微生物生长这一因素对产电量的影响，未考虑MFC中存在混合菌种微生物的情况，忽略了生物膜固体与阳极电极间的传荷阻力，忽略了微生物内源呼吸产生的电子。

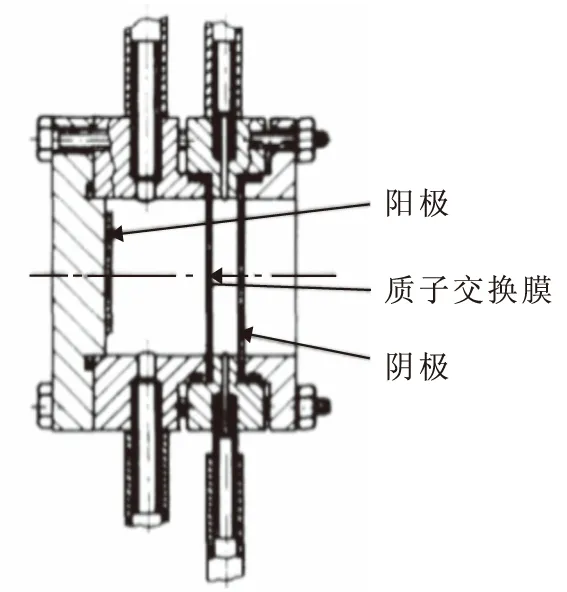
图1 经典MFC单室模型Fig.1 Classic single-chamber model of MFC

随后，Kim等[13]提出了一些特殊微生物可以进行电子转移的设想。实验表明，厌氧生长的Shewanellaputrefaciens菌株表现出电化学活动。这一设想被Picioreanu等[14]的三维混合物种模型所证实。

2.2 多维稳态混合物种模型

Picioreanu等[14]利用Monod方程、Nernst方程、Butler-Volmer方程建立的三维混合物种模型描述了悬浮微生物、附着微生物和多种可溶解微生物在氧化还原介质上的生长情况。该模型可以精确算出不同条件下电流及电压的产出量，并可给出各条件下电压、底物消耗量和微生物增长量等参数之间的关系。依据实验，他们提出介质浓度和醋酸浓度会影响产电微生物和产甲烷微生物的生长，微生物在阳极室可以进行电子转移，这些为后期研究提供了有力的理论基础。该模型的优点在于，利用偏微分方程详细地描述了生物膜阳极混合物种的情况，考虑到阳极产生的质子可能会酸化，从而导致MFC产电量不准确，引入了pH值这一变化参数，使得计算结果更加精确；不足在于，该模型只适用于理想的较薄的细胞膜和扩散系数较大的介质，并且模型复杂、计算时间长，从而较难投入到实际操作中。

Picioreanu等[14]还利用Nernst-Planck方程构造了多维模型，描述了pH值、溶质浓度和生物膜随时间产生的电流的变化，讨论了pH值及电极形状对产电效率的影响，模拟了单物种、多物种电活性生物膜在多孔电极上的附着状况。该模型的不足在于，忽视了离子迁移、流体运动及热传递对MFC产电效率的影响。针对这两点不足，Babauta等[15]提出通过测定同一生物膜的pH值和氧化还原电位来验证该模型的合理性。Osman等[16]提出以葡萄糖氧化酶为基础的二维模型，也可以解决上述模型存在的问题。

表1 MFC数学模型表达式一览

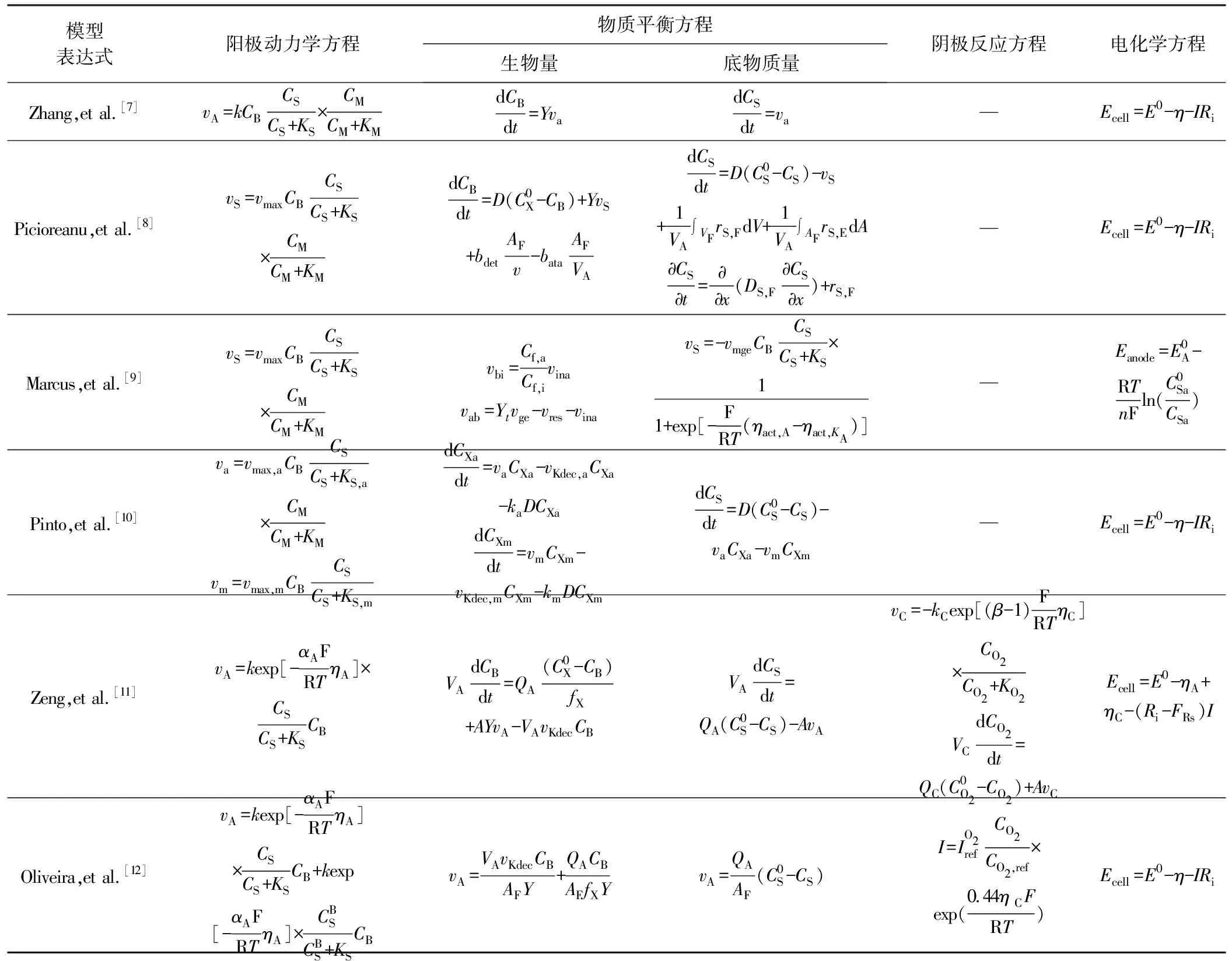
Tab.1 Mathematical models of MFC

2.3 动态混合菌种生物膜模型

Marcus等[9]构建了一维动态混合菌种生物膜模型，创新性地利用生物膜细菌的基质接收、传递电子。该模型假设通过固体基质传递电子的产电细菌有阳极潜在损失，无论生物膜是否活跃，都会争夺阳极表面的空间。他们描述了底物利用率和底物浓度/电势变量之间的关系，为电子供体的氧化速率、浓度和电势间的关系提供了理论支持。该模型的优点在于，详细描述了MFC阳极发生的电化学反应，并阐述了MFC生物膜产电细菌浓度和极化电位的局限性；不足在于，没有考虑阳极室内多个微生物种群争夺相同底物的情况，没有考虑活化损失、欧姆损失、浓度损失及扩散限制[17]。在Marcus模型基础上，Torres等[18-19]通过建立新模型证实并计算了阳极存在的潜在损失，同时高效准确地测量了电导率。Merkey等[20]在Marcus模型基础上利用Nernst-Monod表达式创建了一个二维混合物种模型，讨论了散装液体、固体电极及用矩阵参数定义的生物膜电导率对产电量的影响，阐述了最佳阳极毛耗。Hamelers等[21]将Nernst-Monod方程和Butler-Volmer-Monod方程进行了对比，发现后者与实验数据更相洽，且可预测到零电流。Sedaqatvand等[22]在Marcus模型的基础上通过整合遗传算法建立了环形MFC单室模型，最大限度地减少了模拟的差异性，适用于模拟运行的批处理。Jayasinghe等[23]将基因组规模代谢模型和Marcus模型结合起来，建立了二维混合物种模型。他们讨论了微生物及生物呼吸量对产电效率的影响、空间异质对生物代谢的影响，认为生物膜的电导率并不是限制物质传输的因素。

针对Marcus模型中未考虑阳极室内多种微生物争夺底物的情形，Pinto等[10]提出了一维两种群混合模型，阐述了阳极产电微生物和产甲烷微生物在MFC中竞争相同底物的过程：高外部阻力利于产甲烷微生物的生长，当外部阻力低于或等于内部阻力时，则更有助于产电微生物的生长。此外，他们将电荷的传输机制假设为一种发生在细胞内的传输过程，利用Nernst-Monod方程计算浓度损失，利用Butler-Volmer-Monod方程计算内部介质浓度和活化损失。该模型的优点在于，通过改进依赖于阳极微生物生物量密度的电化学参数，提高了预测的准确性，易于实践，可优化和实时控制操作流程；不足在于，忽视了生物膜的浓度梯度，忽视了将电子传递到阳极进行反应的介质[24]。为进一步优化产电量的影响因素，Hernández-Fernández等[25]在前期模型的基础上建立了新模型，并讨论了单产电微生物、单产甲烷微生物、两种微生物共生三种情况下的底物消耗率，得出结论：在较高浓度的废水中，产甲烷微生物消耗底物的速率要大于产电微生物，通过调节两种微生物的比例可达到最佳产电状态，且串联的MFC有利于提高产电效率。

Recio-Garrido等[26]在Pinto模型的基础上建立了新的生物电化学模型，可以描述MFC的快、慢两种动力过程，还可以通过“离线”、“在线”两种模式进行模拟，前者适用于优化各操作条件，后者可利用已知MFC输出电压来估计模型的其它具体参数。两者结合的新模式有利于更精确地模拟快、慢两种动力过程，同时有利于预测底物浓度的输出。

以上代表性单室模型，虽存在影响因素单一、计算过程复杂等不足，但可为后续模型发展提供有力的理论支持和构建基础。

3 含厌氧室、好氧室的MFC双室模型

MFC双室模型是在同时研究阴、阳两极双室反应进程的状况下讨论MFC的控制因素。双室MFC结构为“H”型 ，两边为阳极室和阴极室。阳极室由阳极和产电厌氧细菌构成，其中为保证产电厌氧细菌的生存，常在阳极室内充有一定量的惰性气体。阴极室由阴极材料和催化剂构成，两室之间由质子交换膜间隔的通道连接。经典MFC双室模型见图2。

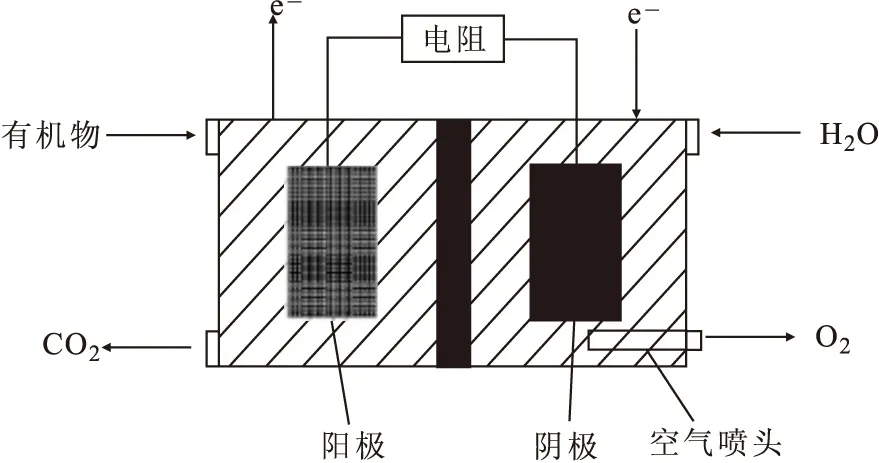
图2 经典MFC双室模型Fig.2 Classic dual-chamber model of MFC

Zeng等[11]通过综合生化反应、电荷平衡来模拟MFC的稳态和动态行为，用Monod方程结合Butler-Volmer方程和Nernst方程在阴极和阳极分别建立模型，构建了一维单物种数学模型，讨论了电压、功率密度、燃料浓度等多个参数对产电效率的影响，同时引入了阴极电子传输系数这一关键影响因素。该模型的优点在于，具有可操作性，有利于微生物燃料电池规模化发展；不足在于，该模型不能深入研究阳极侧生物膜的形成，没有考虑扩散因素及微生物对底物及空间的竞争影响[27]。在Zeng模型框架的基础上，Sirinutsomboon[28]利用纯度较低的基质来建模，用菲克第二定律描述了氧气、蔗糖、质子的扩散过程，深入探讨了生物膜活性对MFC产电量的影响。

Oliveira等[12]利用Monod方程和Tafel方程建立的MFC双室一维单物种模型，除了电荷平衡、质量平衡、生物膜生长和氧化还原反应等常规要素外，还研究了热传递对MFC的影响，考虑了阴阳两极的热平衡及热损失。该模型的优点在于，可以计算整个电池内温度在阳极电极、生物膜、阳极液、阴极液、阴极电极的分布；不足在于，忽略了生物膜的浓度梯度及对流过程，仿真结果表明其阴极过电位过高，并且会随着电流密度增大而上升。

Ou等[29]提出利用Nernst-Monod方程和Nernst-Planck方程分别在阳极和阴极建立一维混合物种模型，阳极稳态模型用来讨论化学物种的扩散和电子迁移对产电量的影响，阴极模型用来得出功率密度和极化曲线，两极室结合来讨论MFC的产电性能。该模型的优点在于，提出电化学活化、欧姆电阻、物质运输损失、衬底交叉是影响阴极室工作的主要原因；不足在于，提高电流时，阴极过电位的增加量是阳极过电位的两倍。

相比单室MFC，双室MFC产电功率密度较低，在以往的模型研究中双室模型没有得到重视，但此类模型对于产电因素的确定具有重要意义。后期双室模型需进一步确定影响产电量的因素，并研究生物膜对产电过程的影响。

4 结语

MFC数学模型研究的发展趋势主要包括以下几个方面：(1)从最初的单菌种研究到后期的多种群菌种研究，对微生物种群的研究逐渐呈多样性；(2)从忽视生物膜影响的Picioreanu模型到研究生物膜电导率的Marcus模型，对生物膜性质的优化研究在不断进行；(3)从忽视微生物生长对产电量影响到对温度、pH值等多重影响因素的研究，对MFC产电影响因素的研究在不断细化。此外，微生物的代谢方式、细胞内电子传递方式、内部细胞抗性、不同离子的膜透性、生物膜浓度梯度等因素对产电量影响的研究仍有待深入。

目前，MFC的主要问题是产电性能不够理想，而优化构型是提升其性能的经济有效的方法。强化传导介质、提升比表面积和降低内阻等方法通常用于单室MFC的改进，而组建多室 MFC和构建MFC电池组则是提升性能的良好方法。在实践中常常是通过阳极立体化、减小电子传递距离等措施来实现的。综上，MFC相比传统能源，具有环保性强、利用率高、安全性强等优点，具有十分光明的应用前景。