圆中的基础图形

郭振钦

【摘要】初中数学教学要以发展学生数学核心素养为导向，突出数学本质，应关注内容主线之间的关联以及同一个内容主线中重要知识点之间的关联。注重知识背后的数学思想、方法的贯通，注重形、数之间的结合，引导学生进行学习内容逻辑线索的梳理。本篇借助圆中的基础图形，引导学生进行一题多解，一解多题。进一步强化在数学实践活动中综合运用数学知识的能力。

【关键词】核心素养  圆  直角三角形

【基金项目】本文系福建省中青年教师教育科研项目研究成果，项目编号：JZ180233（福建教育学院资助）。

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2020）02-0129-02

初中几何学习“始于点，而终于圆”。圆象征圆满、完美，也有自在的含义。初中几何最后一章为圆的学习，实际上是新旧知识间的融合，是总结，也是一种包容。如何让我们在圆的学习中自在起来呢？简单的以圆中的直角三角形为切入点，略谈一二。

在圆中构造直角三角形是一种重要的解题技能，圆中一些题目，添线构造直角三角形，可使隐含条件显露，将分散条件集中，从而帮助学生迅速打开思路，化归到解直角三角形。而在圆中构造基础图形——直角三角形，初中阶段最常见的是垂径定理和直径所对的圆周角为直角这两种方法。

同样的直角三角形，垂径定理的应用侧重于求边与边之间的关系，而直徑所对的圆周角更侧重于角度有关的计算。但在圆的综合应用中，这两者的关系并没有分得那么细，更取决于学生当时的第一反应。而学生的反应与判断则来源于平常的学习和探究。如何提高学生的数学思想及解题能力？这就要求教师平时要帮助学生进行归纳总结，借助圆中的基础图形，引导学生进行一题多解，一解多题，进一步自我提升，择优解题。

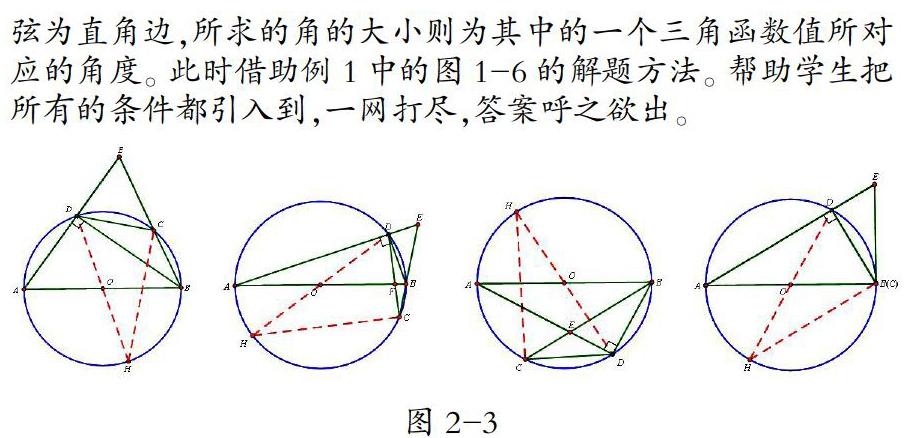
对于第2小题，参考第1小题的方法，让学生去发现圆上的弦CD在动，实际是位置的变化，但形状并没有变化，等式关系依然存在。最终2个问题呈现在我们面前的实际上是这样一种情况（图2-3）。从例1延续到例2，实际上是一解多题的呈现。

一题多解，可以开阔学生思路、发散学生思维，使学生学会多角度分析和解决问题;而多解归一，可以加深学生对数学原理、通性通法的认识，提高解题技巧与能力。这些想法，做法要得以实施，需要我们在日常教学中，依托基础知识，逐步推进，让学生“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”。

参考文献：

[1]《福建省初中学科教学与考试指导意见》

[2]《数学例题》

[3]《泉州中考真题》

[4]《山东中考真题》