儿童哲学视野下质疑能力的培养

何佳

摘要：质疑能力低下已经成为中国学生素养的一个缺陷。究其原因，传统的教学模式使学生的思维形成了定式，严重制约了学生思维的发展。基于儿童哲学视野，结合数学实验教学案例，从实践层面进行策略架构，在实验课中通过鼓励、批判、问学等方式培养学生的质疑能力。

关键词：儿童哲学;质疑能力;小学数学实验教学

20世纪70年代，美国著名哲学家李普曼创建了“儿童哲学”，其主要的意义是为儿童提供哲学训练，使儿童学会像哲学家那样思考，从日常思维转向反思性思维，从不假思索转向深思熟虑，从常规思维走向批判性思维[1]。《义务教育数学课程标准（2011 年版）》也明确指出教师要经常思考“如何引導学生善于与同伴合作交流，既能理解、尊重他人的意见，又能独立思考、大胆质疑”[2]。

基于儿童哲学和课程标准的要求，我们这样理解质疑能力：学生在认知活动中，对意识到的一些难以解决的、感到疑惑的实际问题，能主动产生怀疑、困惑、焦虑、探究等心理状态的能力。质疑的产生是探索的开始，它有利于培养学生追求科学的精神，有利于发挥学生的创造思维能力。在小学数学教学中培养学生质疑的习惯和能力，是全面推进创新教育的开端，是培养创新型人才的关键[3]。

那么，在具体的数学实验教学中，如何培养学生的质疑能力呢？为此，我们有必要作一些探讨和实践。

一、鼓励：为质疑能力的萌发提供土壤

（一）放飞儿童心灵，细心呵护质疑意识的生发

在日常课堂教学中，时常有学生冒出令人意想不到的质疑发问。如果教师以成人的眼光看学生，那么学生的很多新颖奇特的质疑都可能被忽视，长此以往，学生便会将心中的质疑放在头脑里，不愿将它提出来。

要改变学生这种害怕质疑的现状，就必须创建和谐的师生关系。“放飞儿童心灵”，不是说说而已，而应落到实处。教师要在心灵深处平视学生，用“儿童的大脑”去思考，用“儿童的眼光”去看待，用“儿童的情感”去体验……真正站到学生那边去，走进学生的世界，认真倾听，细心体会，做一个欣赏者、引导者和保护者，鼓励并善待学生的质疑发问，让学生在温馨的课堂中，体验数学学习的快乐和美好。

（二）善待儿童过错，用心保护质疑因子的生长

德国哲学家黑格尔指出，错误本身乃是“达到真理的一个必然的环节”[4]。无论学生提出的质疑有无价值，我们教师首先需要做的是对这种质疑行为给予充分的肯定，然后从学生的质疑中找到积极、合理的因素，从而增强学生质疑问难的勇气和兴趣。

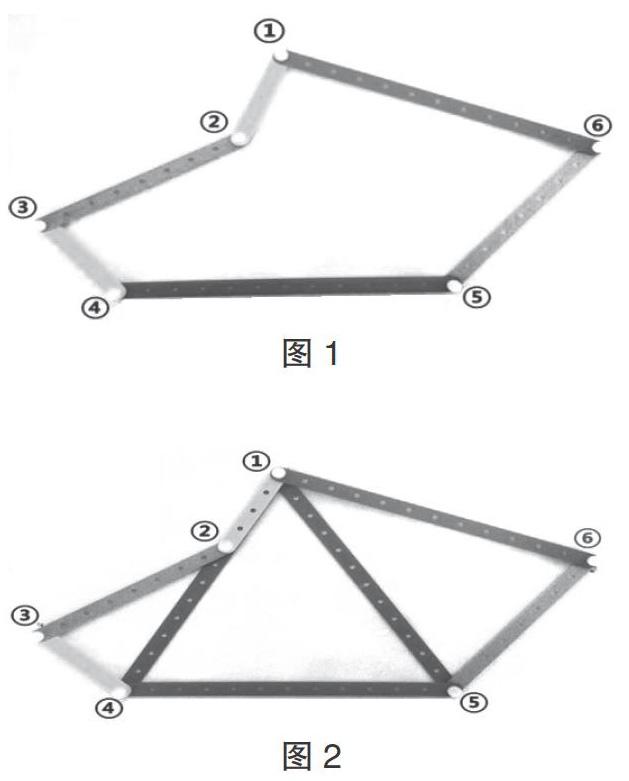
依托苏教版数学教材四年级下册中的“你知道吗”，笔者执教了一堂检验性数学实验课“三角形的稳定性”。在提出“如果要使六边形不变形，至少需要加上几根拼接条？”这一问题后，笔者让学生先猜想，然后动手验证。汇报时，学生们纷纷拿着“成功”的作品向全班同学展示，结果都是“至少需要加上3根拼接条”。正当笔者准备下结论时，“意外”出现了。一位学生举手示意自己找到了反例。怀着忐忑的心情，笔者请他说说自己的想法和做法。只见这位学生拿着“反例”充满自信地跑上讲台，边讲边演示：“这是一个六边形（如图1），用一根拼接条连接顶点①和⑤，再用一根拼接条连接顶点①、②、④，像这样添加两根拼接条（如图2），就能使这个六边形不变形……”全场哑然。笔者在一旁，从“惊吓”到“惊喜”，首先肯定了这位学生敢于质疑的勇气，然后启发全班学生“这到底是不是一个反例呢？”通过全班的探讨，大家发现添加的第2根拼接条与原来六边形的一条边重合了，重合的那条边也相当于是添加了一根拼接条，因此这并不是一个“反例”，而恰恰再一次验证了“六边形至少需要添加3根拼接条才能使它不变形”这一结论的正确性。

教师要从科学的角度理解学生的各种差错，要肯定他们敢于质疑的勇气，评价在对错之外，重在激励学生探究。如此，在课堂上学生才敢于发表自己的意见，教师才能听到学生思维的真实的声音。

（三）激发儿童思考，精心守护质疑精神的生成

学源于思，思起于疑。苏霍姆林斯基说：“教学的技巧并不在于能预见课堂所有的细节，而在于根据当时的情况，巧妙地在学生不知不觉中做出相应的变动。”[5]教学中要因势利导，在学生有疑问，正要提出质疑而苦于不知道怎样表达的时候，真正做到想学生之所想，帮助学生理清思路，明确方向，推动思维的发展，让课堂教学在适时调控中推进。

在苏教版数学教材六年级上册“分数乘整数”的教学中，笔者采用数学实验开展教学，首先直接提出问题：“如果用（b≠0）表示分数，用n表示整数，凭直觉，大胆猜想一下，你认为像这样的分数乘整数，可以怎样计算？”引发学生提出三种猜想：

对这些猜想，笔者给予了充分赞赏和肯定。此时，有部分学生紧锁眉头，似乎对某个猜想感觉很困惑。于是，笔者便顺水推舟，提出问题：这三种猜想都需要一一验证吗？这时紧锁眉头的学生一下兴奋了起来，提出质疑：“猜想①肯定不合理，因为根据分数的基本性质，等式右边还是等于，跟左边不相等。”紧接着，便又有学生质疑：“我觉得猜想③也不合理，根据乘法的意义，等式左边×n表示n个相加，和应该大于，而等式的右边明显小于。”两位学生的质疑赢得了全班学生的热烈掌声。正是因为有了这样的质疑和推想，接下来学生们只需综合运用举例验证、反例求证、演绎推理等方法来验证猜想②是否合理。如此基于课堂生成理念下的课堂教学，焕发了从未有过的生机和活力，一课下来，令笔者感动不已。课堂之所以是充满生命活力的，就因为学生不再是按部就班，被教师牵着走，而是在平等、自由、真诚的对话场景中敢于猜想、质疑，勇于探究、实践。

二、批判：为质疑能力的生长撒下良种

（一）转变，让儿童从“看客”走向“创客”

数学学习中，以节约时间提高效率为由，许多课堂都是以教师的讲解演示居多，学生扮演的大多是看客，没有真正亲身经历数学学习的完整过程，因此便没有了内心真切的想法，质疑能力也就慢慢消退了。而数学实验则是以学生的个别学习为基础的一种学习方式，学生能全员、全程参与到探索和研究活动中去[6]。学生经历知识的再创造，有了深切的体验和感受，对于与自己不同的想法自然便能提出自己独特的见解。

教学“三角形的稳定性”，笔者为每个学生准备了实验所需的工具——拼接条，并且通过开展序列化的实验活动，让学生通过猜一猜、围一围、比一比、拉一拉、说一说等环节，数学化地经历三角形稳定性的建构过程，帮助学生经历数学知识发生、发展的过程，形成自身对此内容的个性化理解。探讨如何在不改变四边形四条边的情况下使得四边形不变形时，联系三角形的稳定性，学生容易想到添加一根拼接条分出一个三角形，便可以使四边形不变形;但个别学生在实际操作中提出质疑：添加一根拼接条将原来的四边形分成了两个四边形后，也“拉”不动（如图3）。这一质疑声引起了全班学生的热烈讨论和深入思考。一石激起千层浪，因为一个特例，激发一群学生的好奇心和探究欲，带动了学生“疑中精进”……在这样的数学实验课堂中，学生俨然从问题的看客变成新知探索的创客。

（二）逆袭，让儿童从“习惯”走向“反思”

习惯性思维是根据自己的经验形成某些结论。教师培养学生的质疑能力，首先要改变学生的思维习惯。教学苏教版数学教材六年级上册“动手做”中的内容——“长方形面积的变化”时，笔者提出“如果长方形的长增加，宽减少，面积会有怎样的变化呢？”大部分学生看到一个量增加，另一个量减少，不假思索地认为面积不变。静静等待15秒后，一个学生提出质疑：“面积变了，虽然分率都是，但是它们的单位‘1不相同。我们可以通过数学实验来解决这个问题。”果然，学生们通过画图、大量举例、用字母推理、利用数学模型等（如图4）进行分析后，发现面积减少了。

（三）生发，让儿童从“定式”走向“发散”

教学的主要任务不是积累知识，而是发展思维。在日常教学中，师生都容易形成一套固定的考虑问题的模式和与之相适应的经验，即思维定式。思维定式有时会禁锢思维，造成思维的惰性，成为质疑能力最大的障碍。教师应鼓励学生灵活调整原来的思维方式，改变思考问题的角度和方向，按照不同的思路来分析、解决问题。

在教学苏教版数学教材三年级下册“长方形和正方形面积的计算”时，其中有一个环节：正方形的面积可以怎样计算？学生思考后，一般会呈现这样的方法：用边长1厘米的小正方形铺满正方形（如图5①）。教师在肯定学生的这种方法后，顺势提出质疑：“有的学生准备的小正方形比较少，铺不满怎么办呢？”立马有学生想到：用边长1厘米的小正方形铺一行和一列，就能知道每行有几个，有几行，同样能得出正方形的面积（如图5②）。还有学生提出：“我没有用小正方形去铺，也可以得出正方形的面积计算公式，我是依据‘正方形是特殊的长方形直接推理证明的（如图5③）”……看似不经意的质疑让学生的思维变得活跃，有效地训练了学生的发散思维。教师以实验的方式，让学生在亲自经历实验的过程中，真实体验知识的产生和形成过程。

三、问学：为质疑能力的成熟续足养分

培养学生的問题意识是学生形成质疑能力的前提和基础。教师要鼓励学生敢于提问，善于提问，激励学生因问而学、善问而学，从而达到问学合一。

（一）引导“善问而学”，在实验中质疑和反思

《礼记》中指出：“善问者如攻坚木：先其易者，后其节目;及其久也，相说以解。不善问者反此。”[7]培养学生的问题意识是学生形成质疑能力的前提。教师的教学设计不仅要考虑自己教得方便、教得精彩、教得舒畅，而且要更多地思考学生如何“学”，突出学生自己提出问题、解决问题的过程，课堂教学的顺畅性在动态生成的互动学习中真实发生。

教学苏教版数学教材六年级上册“长方体的体积”这一课时，笔者确立了“立足于学生的已知，激发起学生灵动的思维”的教学追求，让学生知无不言，言无不尽。大部分学生在学之前就已经知道了长方体体积的计算公式，但少数学生很困惑，提出质疑：“为什么长方体的体积等于长乘宽乘高呢？”这一问题催生了学生有价值的探究。接着根据大部分学生初步探究的困惑状况，教师指点迷津：“我们能不能运用实物进行操作呢？”，让学生在实验中自求自得。通过实验，学生各抒己见。观点在碰撞，智慧在飞扬，对体积公式的理解步步深入。在质疑和反思中，学生们的操作能力、思辨能力、表达能力都得到了提高。整个实验活动过程本质上是一个引导学生不断克服困难，经历自主探索，形成良好思维品质的过程。

（二）提倡“刨根问底”，在实验中推演和论证

李普曼认为，儿童带着强烈的好奇心和求知欲进入学校，而这种好奇心和求知欲在随后的学校生活中消失殆尽，这是传统教育的结果[8]。作为教师，我们要充分开发儿童身上的潜质，鼓励他们不断质疑答疑，刨根问底，教会他们思维。

教学分数加减法练习时，有这样一个题组：

学生通过观察、计算，不难发现：分子是1，分母只有公因数1的两个分数相加减，得数的分母是两个分母的积，分子是两个分母的和或差。教学在这便结束了吗？不！这只是根据4个例子得出的一个猜想，还需要进一步的验证。学生举了大量的例子，发现都符合猜想。这时教师引导学生质疑：例子举得完吗？能分别用一个式子来表示这里的加法和减法吗？学生容易想到用字母来表示：+=（a， b）=1和-=（a， b）=1。教学到这可以结束了吧？不！“知其然，知其所以然。”笔者引导学生提出质疑：“为什么这类特殊的分数加减法能得到这么有意思的结果呢？”通过思考、推演，学生很快能联系分数加减法的计算法则进行论证：+=+=（a， b）=1、-=-=（a， b）=1。其实，这类特殊分数的分母的最小公倍数就是它们的乘积，也就是说公分母是它们的乘积，所以分母为两数之积，分子为两数之和或之差。不完全归纳法得出的结论不一定正确，这里“刨根问底”，深入挖掘规律的内在缘由，不仅仅停留在合情推理的层面上，而是让学生联系计算法则，进行演绎推理，证明猜想一定是正确的，从而得出结论。

现代教育家陶行知说：“发明千千万，起点是一问。”[9]只有“问了”，才能深入思考;只有深入思考了，才能不断产生问题……这样，学生的学习能力、探究能力就在“质疑—答疑—再质疑—再答疑”的循环往复中不断提高。

（三）鼓励“标新立异”，在实验中超越和创造

创新精神和创新能力是可以通过教育来完成的，而质疑能力是创新的前提和内核。数学实验教学中，我们教师除了要培养学生的质疑能力和精神，还要创造机会，激发并最大限度地挖掘学生身上的创造潜能，鼓励他们“天马行空”的想法，放飞他们的“奇思妙想”。

笔者在教学苏教版数学教材六年级下册“大树有多高”时，直接抛出问题“我们学校的教学楼有多高？”课前预习过的学生立马回答：“可以利用教学楼的高度与其影子之间的关系来解决这个问题。”其他学生默认。这个问题本身没有唯一正确的答案，笔者鼓励学生质疑、思辨，令人意想不到的是，学生想到了很多其他的办法：将每一层楼的高度测量出来后相加;打電话询问建造大楼的设计师;爬到楼顶，然后放卷尺下来测量;放个氢气球上去，到楼顶时给绳子做上标记，再拉下来量一量……学生的想法独特且有创意，不再被教材中的唯一解法所束缚。实践证明，让学生学会像数学家那样去思考、去表达，能真正激发他们的创造潜能，发展他们的质疑能力。

在数学学习中保有一颗鲜活敏感的心灵，不断追问下去，问题就会层出不穷，创新也会连续不断。

参考文献：

[1]华堂生.儿童哲学的内涵及其哲学预设[J].学前教育研究， 2014（6）：45.

[2]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社， 2011：48.

[3]陈书芳.浅析小学生数学质疑能力的培养[J].亚太教育， 2015（8）：18.

[4]钱燕.借“错”发挥 精彩纷呈[J].小学教学参考，2018（5）：70.

[5]苏霍姆林斯基.给教师的建议[M].杜殿坤，译.北京：教育科学出版社， 1984：222.

[6]张辉.数学实验：小学数学教学的新视界[J].江苏教育， 2015（17）：36.

[7]乐正克.学记[M].高时良，译.北京：人民教育出版社， 2016：6.

[8]郅庭瑾.为何而教——超越知识与思维之争[D].上海：华东师范大学， 2001：90.

[9]周鲁辉.生本课堂模式下小学英语课堂提问的有效设计[J].中国校外教育， 2019（7）：84.

责任编辑：石萍