深挖活用，借题发挥

杨芳铃 顾晴晴

【摘要】教师在教学中要深入研究练习题的题型、内容、结构，要善于对教材中的练习题进行再创造，适当调整、必要补充、合理重组，用好用活这些好素材、典型题。小题大做：对教材的习题进行精细化改编。借题发挥：挖掘教材习题的内涵进行重组活用。大题小做：“偷工减料”，把教材相关联的练习题精选压缩整合。

【关键词】小题大做（改编）借题发挥（重组） 大题小做（整合）

教材中配备的练习题为练习教学提供了好的素材。教师在教学中要深入研究练习题的内容、结构，进行适当调整、必要补充、合理重组，用好这些习题。在深挖活用时，教师要着眼于学生的学习兴趣、知识理解、思维发展、技能形成，努力使练习题精细、多样、新颖，使练习教学走向丰富，走向深入，走向学生。

一、小题大做——使知识的理解走向深刻

教材中有的练习题相对简单，教师可以根据实际需要，进行精细化改编。改编时要考虑单元教学的体系、把握本课时教学目标，更要从细微处入手，挖掘每一道练习题的功能，通过小题大做，设计富有启发性的练习题，让学生学精、学细。

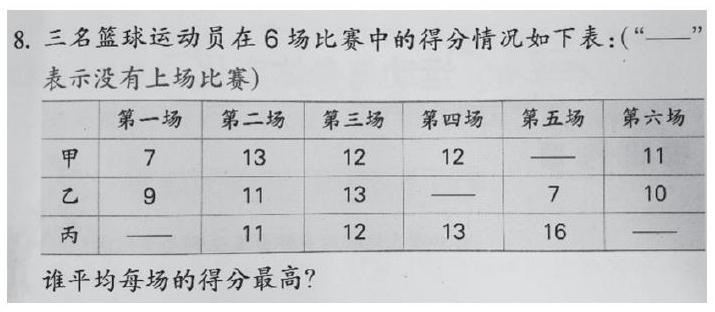
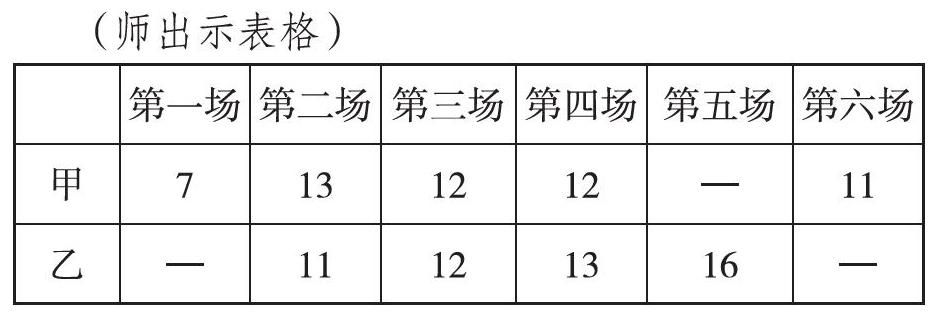
如四年级上册第53页第8题“平均数”练习题，求谁平均每场的得分最高。为了让学生对平均数意义的理解更加深刻全面，让他们感受到平均数既是一组数据的整体反映，又受原始数据的变化而变化，体会平均数与总数之间的联系，教师对这一题进行了改编：

师：不计算，猜一猜甲平均每场得分大概是多少？乙呢？说说你的想法。

生：甲平均每场得分比12分低，乙平均每场得分比12分高。把甲的第二场13分给第六场1分，那么有4个12分，第一场是7分，所以平均每场得分会比12分少。把乙第四场13分给第二场1分，那么有3个12分，第五场是16分，所以平均每场得分会比12分多。

（2）计算判断，谁平均每场得分高？

生：甲： （7+13+12+12+11）÷5=11（分），乙：（11+12+13+16）÷4=13（分），11分<13分，乙平均每場的得分高。

师：为什么计算甲平均每场得分除以5，乙除以4？

生：上场场次不同。

（3）如果丙平均每场得分也是11分，估计他第三场得了多少分？

生：应该比11分多。因为9分和7分比11分少，所以第三场只能比11分多，平均分才能达到11分。

师：丙第三场到底应得多少分？

生：11×4=44（分），44-（9+11+7）=17（分）。

（4）填空：在横线上填大于、等于或小于。

假设丙参加了第六场比赛：

如果第六场得分是11分，那么平均每场得分          11分，如果第六场得分是6分，那么平均每场得分          11分，如果第六场得分          11分时，那么平均每场得分大于11分。

师：这一题给你什么体会？

生：每一场次的得分都会影响到平均分。

（5）要使每场平均得分提高1分，那么第六场应多得           分，为什么？

生：要比11分多得5分。因为平均得分提高1分，相当于每场都提高1分，1×5=5分。

改编由一问到五大问，为学生搭建了一个思维平台。既有从总数到平均数的顺向思考，又有根据平均数推断总数的逆向思考，学生思维在顺向与逆向的问题之间转换，不断深化对平均数意义的理解。

二、借题发挥——使思维的发展变得灵活

教材中的每道习题都有其独特用意，但是受书面限制，呈现形式可能比较单一，这就需要教师挖掘其内涵，进行活用。教师要抓住教材重点和难点，围绕学生学习中的薄弱之处、关键之处有针对性地设计开放性、多元化的练习题，激活学生思维，合理编排练习梯度，借题发挥强化练习，让学生学实、学活。

二年级下册“两位数加两位数口算”第60页想想做做，共有五题。如果教师按照教材的编排依次进行练习，会形成单调乏味的计算疲劳感和被动状态。而且，本课是在学生学习了两位数加两位数进位加笔算的基础上教学的，可以对这些练习题进行升级，以促进学生形成口算技能，提升思维水平。于是在学生完成想想做做第1、2题的基础上，教师对教材中的第3、4、5题练习题做了如下重组：

第3题：请说出下面算式的得数是几十多。

54+14      6□+25      49+37      32+4□

其中，6□+25和32+4□两题具有一定的开放性。由于一个加数个位上的数不确定，这就促使学生运用已有经验去分析不同的情况：当个位上相加不满10，那么得数就是八十多，当个位上相加正好等于10，那么得数就是九十，当个位上相加超过10，那么得数就是九十多。

第4题：出示商店购物主题图，玩具飞机每架37元，玩具汽车每辆42元，玩具轮船每艘2□元。

师：请小朋友根据线索：37+2□=6□（元），猜猜一艘玩具轮船可能是多少钱？你是怎么想的？

猜价格让学生经历了一次逆向思维，有效突破了进位的难点：根据得数6□，观察两个加数的十位上是3+2=5，判断这是一道进位加法题，从而判断出个位上7+□应该满10，再来猜一艘玩具轮船的价格可能是多少元。

猜完，教师揭示一艘轮船的价格是29元。然后提出第二问，你喜欢购买哪两样玩具，共应付多少钱？

第5题：班级选拔跳绳运动员，有四名同学参加了选拔，成绩如下表：

（1）你首先会选谁参加比赛？

（2）强强和军军，你会选谁参加比赛？你怎么想的？

（3）出示数据，计算四名运动员共跳了几下？

这题的设计更加开放，留给学生思考的空间更加宽广。特别是第二问，学生在选的时候，乍一看都会选军军，因为军军是四十几加三十几，而强强是三十几加三十几。但仔细分析会发现，如果三十几加三十几的个位上都是比较大的数，就有可能是进位加，那么得数也会是七十多;而如果四十几加三十几的个位上都是比较小的数，就有可能是不进位加，那么得数也是七十多，这样一共的个数也有可能强强多于军军。最后公布数据，通过计算，发现强强一共跳了78下，军军一共跳了75下，果然强强比军军跳得多。

这样的重组，始终围绕着进位加这一重难点。但是形式多样了，有助于激发学生的学习兴趣。问题开放了，有利于开启思维的阀门。学生在这样的练习中扎实算法，发展数感，丰富经验，逐步走向算理算法融会贯通。

三、大题小做——使应用的意识成为自觉

教材中的习题层次分明，要求明确。但有时，也因为明确而少了一点自觉意识。这时教师不妨来个“偷工减料”，把相关联的练习题精选压缩整合到一起，以大问题形式抛向学生，引发思维冲击，让学生在领悟方法和锻炼能力中学通、学透。

以上是四年级下册第38页整理与练习第1～3题，属于第三单元三位数乘两位数的练习题。如果按书上的习题进行教学，第1题学生会口算，第2题会用竖式计算，第3题会根據积的变化规律写出得数，看上去十分顺利。但是，学生活用口算、估算、竖式计算的意识没有得到很好的培养。因此，教师把这3题优化组合成一组习题，进行如下整合：

出示：

14×300         198×72          308×61

14×150         580×19          40×201

师：如果想知道这些算式的得数，你会用什么办法？

生1：竖式计算。

生2：有些可以直接口算，有些需要竖式计算。

师：你能找出哪些算式可以直接口算出得数的？口算出结果。

生：14×300=4200，40×201=8040。

师：你是怎么想的？

生：14×300可以看作两位数乘一位数14×3=42，得数后添2个0，40×201可以看作三位数乘一位数，4×201=804，得数后添1个0。

生：14×150也能口算出结果，等于2100，因为14×300=4200，150是300的一半，14×150的得数也是4200的一半。

师：通过刚才的计算，你有什么发现？

生：先仔细观察，再灵活运用计算方法，可以提高速度。

师：请你把剩下3个算式的得数从大到小排排队。

198×72     308×61    580×19

（师巡视，有的学生开始进行竖式计算，有的则很快排好顺序了）

师：你怎么这么快就排好了呢？

生：我把198×72看成200×70=1400，把308×61

看成300×60=1800，把580×19看成600×20=12000，只要估算就可以知道它们的得数大约是多少了。

师：你怎么会想到用估算呢？

生：因为只要知道得数的大概大小就能排出大小，不必要知道精确得数。

师：这道题告诉你什么经验？

生：如果不需要精确的结果，那么可以运用估算快速解决问题。

师：想知道198×72的实际得数比1400多还是少，可以怎样？

生：用竖式计算出得数。

如此整合，看似习题少做了，实则学生自主运用知识的选择多了。学生在解决这些问题时所展现出来的应用意识、思维水平是不同的，正是这些不同的表现，在学生之间形成了思维冲击，一部分学生获得了成就感，一部分学生受到了启迪，感受到了口算、估算、竖式计算的各自用途，也强化了自觉运用的意识。