展示图形无穷魅力?培育几何直观素养

《义务教育数学课程标准》（2011年版）明确指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。”如何借助几何直观促进课堂教学改进，使学生真正地深度学习，本文以教材中一道例题的教学为例，展示培育学生几何直观素养的重要性。

一、问题呈现

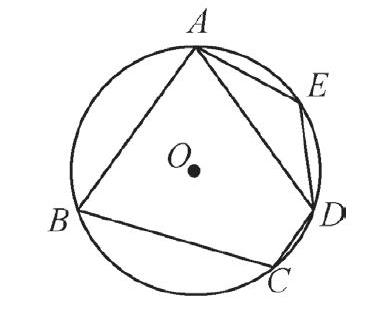
（苏科版教材九年级上册第二章2.4圆周角第59页“例4”）如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=110°，若点E在上，求∠E的度数。

二、教学分析

本题要求∠E的度数，常見的教学方法是教师引导学生先观察图形，根据题目的已知条件和要求，找出它们之间的关系，为正确解题做准备。教师如果尝试将例题的条件减少，那么题目的难度自然就降低，同时图形也由繁变简。教师如果再尝试将例题的条件改变，那么题目难度降低的同时，图形也变为学生有认知基础的图形。学生就可以依托看到的图形进行思考，展开想象，探索解决问题的思路，预测结果。因而帮助学生提升几何直观能力应成为教学中关注的目标。

三、教学过程

环节1 理清条件要求

请分析例题的条件与要求。

分析：审题是解题的前提，通过审题，分析例题的条件和要求。本题的条件是在⊙O的内接四边形ABCD中，AB=AD，∠C=110°，若点E在上，要求∠E的度数。根据题目的已知条件和要求，找出它们之间的关系，为正确解题做准备。

环节2 降难简化图形

（1）降低例题的难度，即减少一个已知条件，例题将变成什么问题？

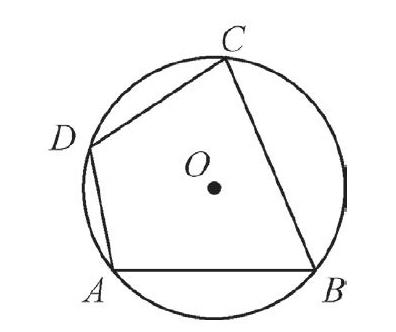
（2）如图，在⊙O的内接四边形ABCD中，∠A=110°，求∠C的度数。

分析：将例题的条件减少，可以降低题目的难度，同时图形也由繁变简。例题的条件有两个：一个是“AB=AD”，另一个是“∠C=110°”。将例题中的已知条件“AB=AD”删除，将“∠C=110°”更改为“∠A=110°”，求“∠E的度数”更改为求“∠C的度数”，即问题（2）。如何解决问题（2）呢？学生尝试利用“圆内接四边形的对角互补”，因为∠A+∠C=180°，所以∠C=180°-∠A=70°。降低例题的难度，简化图形，学生成功解决问题（2），为解决例题打下了坚实的基础。

环节3 借助图形思考

（3）改变例题的已知条件，例题将变成什么问题？

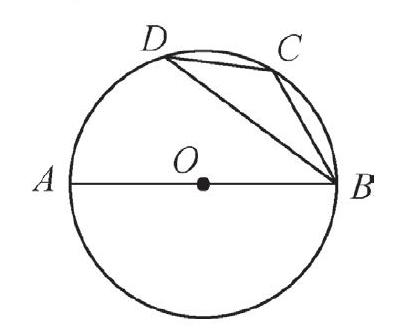
（4）如图，已知AB为⊙O的直径，点C、D在⊙O上。若∠ABD=30°，求∠BCD的度数。

教学片段1：

教师：例题的已知条件改变了，你们能谈谈哪些条件改变了吗？

学生1：例题中的已知条件“AB=AD”更改为“AB为⊙O的直径”，“∠C=110°”更改为“∠ABD=30°”，求“∠E的度数”更改为求“∠BCD的度数”。

教师：你们能解决问题（4）吗？

学生2：条件改变后，题目的难度降低了，图形也是之前熟悉的图形。连接线段AD，由直径所对的圆周角是直角，就构造了Rt△ABD，得∠ADB=90°，则∠DAB=90°-∠ABD=60°。根据“圆内接四边形的对角互补”可得出∠BCD=180°-∠DAB=120°。

教师：这位同学通过添加辅助线，巧妙解题。连接线段AD的原因是什么？

学生2：通过观察图形，我发现图中缺了条线段AD，因为直径所对的圆周角是直角，线段AD既是直角三角形的边，也是⊙O内接四边形ABCD的边。

教师：利用数形结合的思想解决问题，很好。你们仔细观察例题的图形，能顺利找到解决例题的方法吗？

学生3：我仔细观察了图形，与问题（4）类似，缺少一条线段。如果连接线段BD，可以构成等腰△ABD和⊙O内接四边形ABDE。因为在⊙O的内接四边形ABCD中，∠BAD+∠C=180°，所以∠BAD=180°-∠C =70°。又因为AB=AD，∠BAD=70°，所以∠ABD=∠ADB=55°。又因为题目中还构造了新的⊙O内接四边形ABDE，所以∠E=180°-∠ABD=125°。

教师：用类比问题（4）的解题方法，用图形思考问题，通过添加辅助线，得到一个⊙O内接等腰三角形和两个⊙O内接四边形，回答正确。

分析：将例题的条件改变，可以适度降低题目的难度，图形也变为学生有认知基础的图形。

几何直观需要逻辑推理的支撑，学生通过看图形，猜想出可能的论证思路，这是学生合情推理能力提升的表现。学生能够类比问题（4）的解题方法解决例题，把抽象的思考对象直观化，这是学生几何直观素养提升的表现。

环节4 寻找基本图形

（5）如图，在Rt△ABC中，∠ABC=90°，点M是AC的中点，以AB为直径作⊙O分别交AC、BM于点D、E，求MD与ME的大小关系？

教学片段2：

教师：能谈谈这个图形由哪些基本图形构成的吗？

学生4：由⊙O、四边形ABED、△ABC、△DME、△ABM、△BMC组成。

教师：你能利用这些基本图形解决问题（5）吗？

学生4：能。因为∠ABC=90°，AM=MC，所以BM=AM=MC，所以∠A=∠ABM。又因为四边形ABED是圆内接四边形，所以∠ADE+∠ABE=180°，且∠ADE+∠MDE=180°，所以∠MDE=∠MBA。同样的方法可证∠MED=∠A，所以∠MED=∠MDE，由等角对等边可得MD=ME。

教师：这位同学能从基本图形出发，利用直角三角形斜边上的中线等于斜边的一半，圆内接四边形的对角互补，等角对等边等知识点解决问题（5），思路清晰。

分析：基本图形是解决数学问题的“足”，无“足”寸步难行，有“足”健步如飞。引导学生从复杂的图形中找出基本图形，依托基本图形解决问题，这应贯穿在学生数学学习的整个过程中，更是教师教学过程中始终关注的目标。

环节5 让图形动起来

（6）如图，圆外接于正方形ABCD，P为上一点，且AP=1，PB=2，求PC的长。

教学片段3：

教师：能谈谈这个图形由哪些基本图形构成的吗？

学生4：由圆、正方形ABCD、△ABP、四边形ABCP等组成。

教师：这些基本图形是对称图形吗？

学生4：圆和正方形既是中心对称图形，又是轴对称图形。

教师：你能利用对称图形的性质解决问题（6）吗？

学生4：能。把△ABP绕点B顺时针旋转90°，得到CBP?。因为四边形ABCP是圆内接四边形，所以∠PAB+∠PCB=180°，且由旋转的性质知∠PAB=∠P?CB，所以∠P?CB+∠PCB=180°，所以P、C、P?三点共线。又因为旋转前后的图形全等，所以P?C=PA=1，PB=P?B=2，△BPP?是等腰直角三角形。根据勾股定理可以顺利求出PP?=4，则PC=3。

分析：常见的图形运动包括平移、翻折、旋转，图形位置的变化可以引起条件或结论的改变，也可以集中分散的条件，为解题提供有利的条件。学生会用动态的眼光看待图形，能够通过改变图形的位置创造条件，便于在新的图形中分析图形之间的关系。

环节6 特殊图形作用

（7）已知：如图，面积为2的四边形ABCD内接于⊙O，对角线AC经过圆心，若∠BAD=45°，CD=，求AB的长为多少？

教学片段4：

教师：能谈谈这个图形由哪些基本图形构成的吗？

学生4：由⊙O、Rt△ADC、Rt△ABC、四边形ABCD组成。

教师：这些基本图形具有特殊性吗？

学生4：有。Rt△ADC、Rt△ABC有特殊角直角，⊙O内接四边形ABCD有特殊角45°，可利用特殊角45°构造等腰直角三角形。

教师：很好。你能叙述解题思路吗？

学生4：延长BC，过点D作BC延长线的垂线，两线交于点E。过点D作AB的垂线交AB于点F。根据问题（5）的解题经验，∠DCE=∠BAD=45°，因此 △DCE、△ADF均为等腰直角三角形。此时，图形中还出现了矩形FBED，根据矩形对边相等，FD=BE，这样线段AD、AB、BC、DC之间的关系就建立起来了，利用Rt△ADC、Rt△ABC的面积和为2就能求出AB的长。

分析：学生通过观察图形、动手画图将抽象的思考对象直观化，直观便于形象思维的展开，为解题开山辟路。逻辑推理能力和几何直观能力的提升都应该是教师孜孜以求的目标。两种能力相互交织的关系，可谓“你中有我”“我中有你”。

环节7 回顾总结通法

请回顾7个环节的全过程，描述我们的历程？

分析：教师引导学生梳理解题方法，总结解题经验，在教学中具有画龙点睛的作用。这个教學环节的实施，让学生具有融会贯通的能力，是教学任务成功完成的表现。

四、教学价值与功能分析

1.养成画图习惯，培育几何直观素养

在教学中，教师要有意识地培养学生画图的习惯，因为图形可以把抽象的思考对象直观化，直观便于把复杂的问题形象化，不仅为学生解题开山辟路，还可以使学生预测结果。如何帮助学生养成画图的习惯？这是一个循序渐进的过程。教师在教学中应不断寻找恰当的契机，鼓励学生画图，再运用图形解决问题;教师引导学生挖掘画图的价值，如学生在解决问题（4）时，教师追问：“你能告诉同学们为什么连接线段AD吗？”就是引导学生挖掘“连接线段AD”给解题带来的价值;教师利用各种途径，如多媒体等，有意识强化画图为后续解决问题和反思交流带来的便利。

2.寻找基本图形，培育几何直观素养

基本图形是构成复杂图形的基本元素，基本图形分为理论型和经验型：理论型基本图形是课本中的概念、公式、定理等所对应的图形;经验型基本图形由两个或两个以上的简单理论型基本图形组合构成。学生最棘手的就是看到复杂图形无从下手，教师作为引导者，应适时点拨学生，如何分解复杂图形，即从复杂图形中分解出基本图形，化繁为简，轻松解决问题。如学生在解决问题（5）时，教师先问：“你们能谈谈这个图形由哪些基本图形构成的吗？”学生找出基本图形后，教师追问：“你能利用这些基本图形解决问题（5）吗？”学生以基本图形为抓手，快速把题目的信息重组，轻而易举解决问题。教学中，教师要有意识培养学生掌握基本图形的习惯，有意识强化基本图形的灵活运用，关注学生运用基本图形发现、描述问题的能力是否提高应成为永恒的目标。

3.利用图形变换，培育几何直观素养

图形变换包括图形的平移、翻折、旋转，图形变换前后的图形位置虽然改变，但大小并未改变，属于全等变换。图形变换后位置、大小均改变，不属于全等变换。教学中，如果遇到题目给出的条件分散或不明显时，可以利用图形变换解决问题。如学生在解决问题（6）时，教师先问：“你们能谈谈这个图形由哪些基本图形构成的吗？”教师继续追问：“这些基本图形具有特殊性吗？”“你能利用对称图形的性质解决问题（6）吗？”学生在教师的引导下让图形动起来，利用图形的旋转，引起图形位置的改变，把题目分散的条件有效整合，顺利解决了问题。学生利用图形变换可以挖掘出题目中的隐含条件，以此为抓手，实现问题实质的突破。教师要有意识地培养学生用动态的眼光看待图形，让图形在头脑中动起来。

4.数形相互转化，培育几何直观素养

几何直观包含图形和直观两层意思，直观不仅指直接看到的东西，更重要的是借助现在看到的和以前看到的东西进行思考和想象，它的本质是一种通过图形所展开的想象能力。几何直观就是依托、利用图形进行数学的思考和想象。几何直观是具体的，与数学内容紧密联系。很多数学内容、概念既有“数”的特征，又有“形”的特征。数形结合包含以数助形和以形助数，“数”与“形”就是数学的左膀右臂，缺一不可。数的严谨性与形的直观性完美结合使复杂问题简单化，因此解题的道路变得平坦。本节课所有问题就是通过数形结合这种思想方法解决的。教学中，教师要有意识培养学生巧用数形结合解决问题的习惯，培育学生的几何直观素养。

刘冬艳   江苏省泰州市明珠实验学校，一级教师。