例谈解析几何中的“隐形圆”问题
2020-05-03许万成
高中数学教与学 2020年5期
许万成
(江苏省建湖县第二中学,224700)
解析几何中的圆在历年高考中都会出现.对于那些简单的圆的问题,很多学生能够快速并且准确地解答;但有些问题的条件中没有直接给出圆方面的信息,而是隐藏在题目中,需要通过分析和转化才能发现的圆,再利用圆的知识来解决问题.后一类问题不妨称为“隐形圆”问题,它常使学生束手无策,需要同学们对此类问题有个清晰的认识.本文举例说明在相关问题中发现隐形圆的常用策略,供参考.
题型1利用圆的定义确定隐形圆




题型2利用动点P对两定点张角为直角确定隐形圆
例2若实数a、b、c成等差数列,且点P(-1,0)在动直线ax+by+c=0上的射影为点M,定点N(3,3),则线段MN长度的最大值是______.
解因为a、b、c成等差数列,所以2b=a+c,即0=a-2b+c,直线ax+by+c=0恒过定点Q(1,-2).




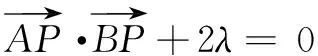


题型4利用两个定点A、B,动点P满足PA2+PB2=D(常数)确定隐形圆.
例4在∆ABC中,A、B、C所对的边分别为a、b、c,若a2+b2+2c2=8,则∆ABC面积的最大值为______.


评注若A、B为动点,动点P满足PA2+PB2=λ(λ>0),很快可得到点P的坐标符合圆的一般方程.






