浅析圆锥曲线中的探究性问题

赵善华

(华东师范大学附属周浦中学，201318)

探究性问题是一种开放性问题,其特点是命题中缺少一定的条件或无明确结论,需要经过猜测、归纳并加以证明的题型.圆锥曲线的探究性问题主要是结论探究的开放性问题,如探究位置关系、研究对象的存在性、定点问题等等,其结果有结论存在和结论不存在两种情形.这类题型在考查圆锥曲线基础知识及几何性质的同时,能很好地考查学生的运算求解、推理论证等数学能力,对学生的综合能力要求较高.本文举例说明求解圆锥曲线中探究性问题的常见解题思路,不到之处敬请同行批评指正.

一、数形结合,注重特殊与一般

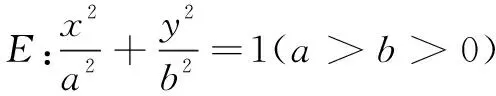
(1)求椭圆E的方程；

(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.

(2)解法1 假设存在定点M满足条件,由对称性可知点M必在x轴上,可设M(t,0).

评注本例在探索定点M的存在性时, 由图形的对称性得到M存在时必定在x轴上,由此可减少未知数的引入，降低问题求解的难度.解法2以特殊情况探路,再对一般性验证,使探索目标更加明晰,能有效考查学生的数学抽象、逻辑推理等数学核心素养.

二、引参消参,借力设而不求

(1)求椭圆C的方程；

(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA、PB、PM的斜率分别为k1、k2、k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.

=2k-1.

评注引参消参、设而不求是求解解几问题的重要方法与手段. 本题通过引入直线AB的斜率k,借助点A、B的坐标为桥梁,用k去表示k1、k2、k3,将k1+k2=λk3转化为关于k的方程.该方程有解，则说明实数λ存在，否则λ不存在.本题也以先考虑特殊情况k=0探索出λ=2,再对一般情形验证.

三、类比推理,优化计算

(1)求C1、C2的方程；

(2)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA、MB分别与C1相交于点D、E.

(i)证明:MD⊥ME;

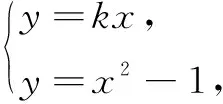
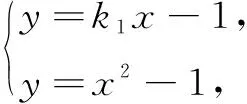
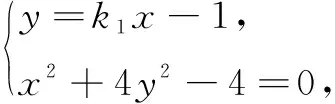
评注本题用k1去表示点A、B、D、E的坐标及面积S1、S2时,根据计算途径的相似性运用类比推理,极大地优化了计算的进程.

总之,圆锥曲线中的探究性问题的常用解题策略有两种：一是先假设研究对象存在或结论成立，然后引进未知数、参数并建立与其有关的等量关系，若能求出相应的量，则表示研究对象存在或结论成立，否则表示研究对象不存在或结论不成立；另一种方法是在假设研究对象存在或结论成立的前提下，利用特殊情况作出猜想，然后加以验证.另外，简化计算过程也是解答解几问题过程中需要考虑的要素.