一类分式型三角函数最值问题的探究

李蓉芳

(甘肃省临泽县职教中心，734200)

求解三角函数的最值问题是高考的热点题型之一.解决这类问题，不仅要用到三角函数的定义域、值域、单调性、图象和三角函数的恒等变形等知识,还常常涉及到函数、不等式、方程、几何等众多知识，综合性很强，许多同学面对这类问题常觉得难以下手.但只要熟悉三角函数的特性,掌握三角函数与方程、导数之间的转化,最值问题也就迎刃而解了．本文结合一道高考变式题,从不同的解题角度,探究该类题型的解题方法．

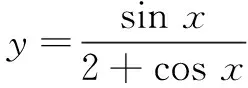
解法1 (利用三角函数的有界性求最值)

∴sinx-ycosx=2y，

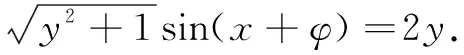
又∵|sin(x+φ)|≤1，

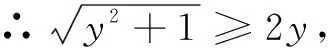
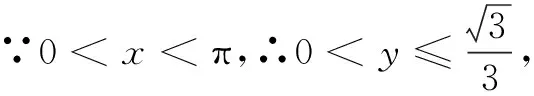
评注 解法1是从三角函数有界性即正弦函数值域小于或等于1出发,对原函数进行变形,利用有界性将三角函数最大值问题变成解不等式．

解法2 (利用二次方程的判别式求最值)

两边平方整理，得

(y2+1)cos2x+4y2cosx+4y2-1=0

Δ=4y4-4(y2+1)(4y2-1)≥0，

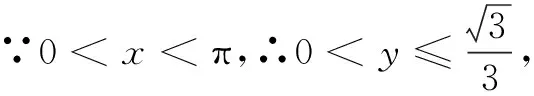
评析 解法2是把三角函数最值问题转化成了同学们掌握更为牢固的二次方程问题．首先对函数进行变化整理,变成一个关于cosx的二次方程,再根据二次方程有解的条件借助判别式解出最大值．

解法3 (利用换元转化为均值不等式求最值)

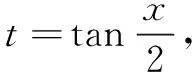
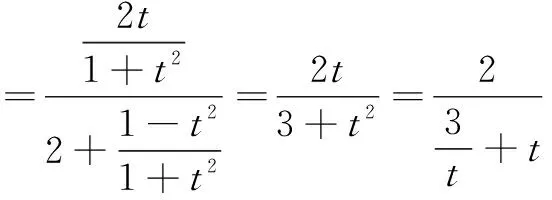
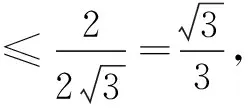
评注 解法3利用换元,将sinx和cosx变成t的函数,使得转化后的函数中仅含一个三角函数,此时再解不等式即可得出最值．

解法4 (利用导数求最值)

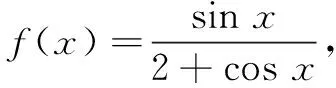
f′(x)

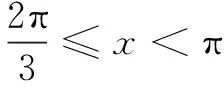
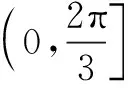
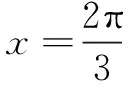
评注 不管是三角函数，还是其他函数,本质上都是函数,所以求三角函数最值问题也都是求函数最值问题．而求导就是求函数最值问题最基本思路之一,故也可用于解答此题．

解法5 (利用数形结合求最值)

如图1的单位圆中,∠MOP=x(其中x∈(0,π).

P(2,0),M(-cosx,-sinx)

PA为单位圆切线,当M位于切点A时,PM斜率最大.

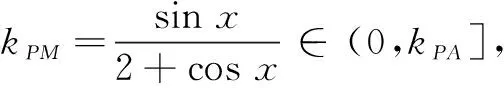
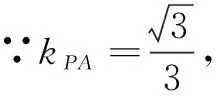
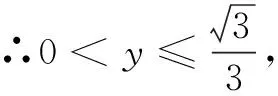
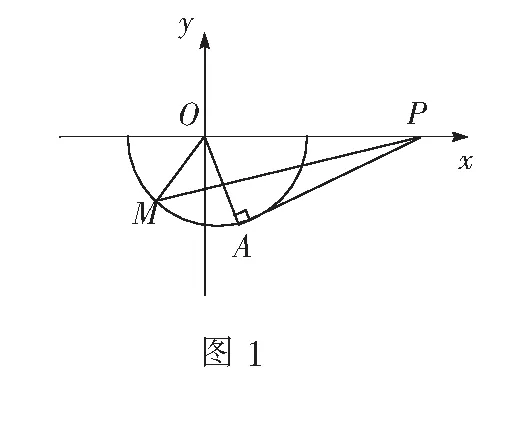
评注 此解法是一种特殊解法,利用了数形结合的思想,将函数问题转化为图形问题,借助直线斜率求得最大值．

综上所述,分式型三角函数的最值问题,对数学思维要求高,综合性强,解法多样,但其基本思路是将最值问题转化为解不等式问题．对于大多数最值问题,可采用解法1、2的解题思路,即通过简单转化,将最值问题转化为大家熟知的三角函数、二次函数等问题,再通过解不等式得到答案,这两种方法都是容易掌握的．解法3需要熟悉三角函数之间的恒等变形,要有一定的变形能力．最后两种方法则是对于某些特别的分式型三角函数有用,可让同学们了解，这有利于思维拓展.总之，如何解决应根据其结构特点灵活选择．