平面几何两个名题及其妙解
2020-04-30李伟帅
李伟帅
(山东省青岛胶州市第八中学 266300)
一、引言
平面几何作为数学王国中重要的一部分,研究者众多,很多有名的数学家,大学教授和学者都研究过平面几何.但关于平面几何名题方面研究得较少,我查资料所得到的结果为:中国学者高希尧著《世界数学历史名题一百例》,中国科学技术大学杜锡录著《平面几何中的名题及其妙解》等.
纵观其研究,大部分学者都是研究古今数学名题供人们阅读或参考,但突出其妙解的材料并不是很多.所以我这次特对部分古今中外平面几何中有名的题目进行巧妙解法的探索,以提高探索解题方法,解题能力,从而进一步认识数学,感受数学思维的巧妙之处,激发同学们对数学学习的兴趣.
二、两个名题及其妙解
1.哥尼斯堡七桥问题
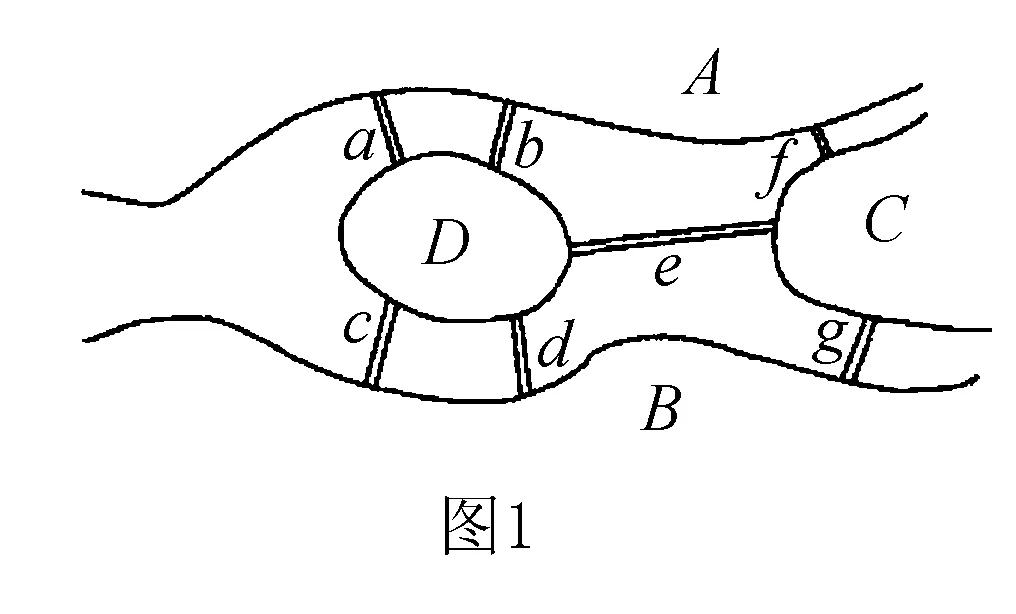
哥尼斯堡镇有一座小岛,一条名叫普雷格尔的小河分两支流进小镇,从小岛两旁流过,然后汇成一支流出小镇,如图1所示.图中D表示小岛A,B,C表示镇中三块陆地.在小岛D和陆地A之间有两座小桥,这两座小桥用a,b表示;在小岛D和陆地B之间有两座小桥,这两座小桥用c,d表示;在小岛D和陆地C之间有一座小桥,用e表示;在陆地A和陆地C之间有一座小桥,用f表示;在陆地B和陆地C之间有一座小桥,用g表示.问题是:能否一次通过全部的七座桥,而每座桥只走一次?
欧拉对哥尼斯堡七桥问题做了详细的研究,于1736年发表了题为《与位置几何有关的一个问题的解》的文章.文章中它给出了判断可能不可能把所有的桥走一次的简单法则:
如果有奇数座桥通过的地方不止两个,满足要求的路线是找不到的;
如果有奇数座桥通过的地方只有两个,满足要求的路线是可以找到的,不过必须从这两座有奇数座桥可通过的地方之一出发,最后从另一座有奇数座桥通过的地方结束;
如果没有一个地方是有奇数座桥通过,满足要求的路线可以找到,并且可以从任何一座桥出发.
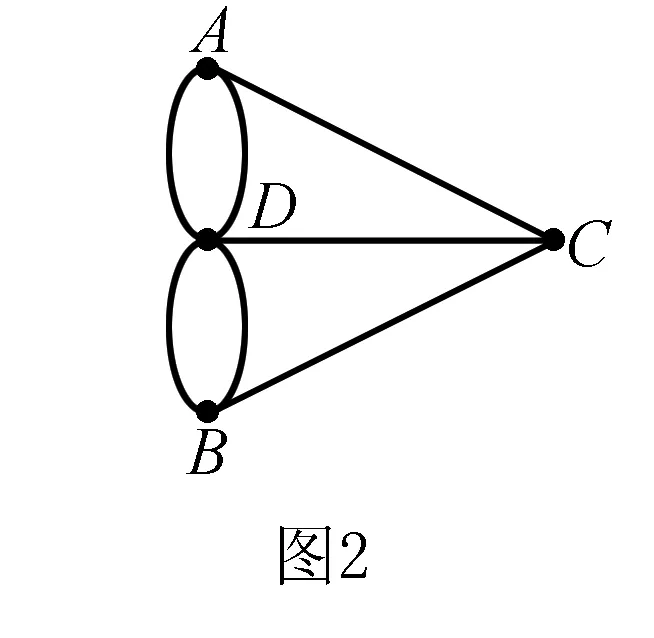
按照欧拉给出的法则,不难知道要想一次通过哥尼斯堡镇的所有七座桥,而每座桥只走一次是不可能的.如果把七桥问题抽象出来,其实它就是一个笔画问题.事实上,由于不关心小岛和陆地的漫记大小,所以可以把它们看做点,而对于桥,由于不关心其长度、宽窄大小,可以把桥看做一段曲线.所以问题就成为:有四个点A,B,C,D,连接D,A有两条线段,连接D,B有两条线段,连接D,C有一条线段,连接C,A有一条线段,连接C,B有一条线段,如图2所示.
问题就转化为能否一笔画画出这个图,每条线段只画一次,而且在画时笔不允许抬起来离开纸.
把所有奇数条线段通过的点叫做奇数点;偶数条线段通过的点叫做偶数点.例如在图2中,通过点A的线段有3条,通过点B的线段有3条,通过点C的线段有3条,通过点D的线段有5条,所以它们都是奇数点.
判断可能不可能一笔画的最简单法则为:
如果奇数点多于2个,则不可能一笔画出来;如果奇数点共有2个,则可以一笔画出来,而且必须从一个奇数点起笔,从另一个奇数点止笔;如果没有奇数点,全部是偶数点,则一定可以一笔画出来,可以从任何一个点起笔,从另外的任何一个点止笔.
2.费马点
费马是法国数学家,1601年8月20日生于图卢斯附近的波蒙特,1665年1月12日卒于卡斯特尔.费马是解析几何的两个发明者之一.在笛卡儿的《几何学》发表之前,他在1629年就已经发现了解析几何的基本原理.费马被誉为近代数论之父,他提出了“费马大定理”,之后三百多年,最优秀的数学家都未能给出一般性的证明,直到1994年“费马大定理”才被英国数学家怀尔斯给出了严格证明.
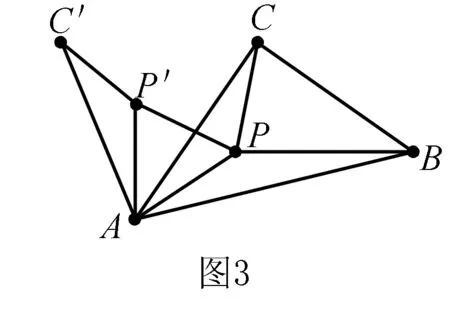
费马点已知△ABC,找一点P使得PA+PB+PC的值最小(图3),这个点P称为△ABC的费马点.
下面给出的一个简明的解法是巴克纳给出的,我们就锐角三角形的情况讨论.
证明P是锐角△ABC内任意一点.把△ACP绕A点旋转60°,得△AC′P′,使AC在AC′和AB之间.
∴△APP′是等边三角形,∴PP′=PA,P′C′=PC.
∴PA+PB+PC=PB+PP′+P′C′.
∵AC′=AC, ∠C′AC=60°,∴C′是一定点.
∴当P点在BC′上时,才有BC′=PA+PB+PC为最小.
∵∠APC′=60°,∴∠APB=120°,同样可知,当∠APC=∠BPC=120°时,PA+PB+PC为最小.
