遗传-蚁群算法在智能交通中的应用

胡清准，邱晓晖

(南京邮电大学 通信工程学院，江苏 南京 210003)

0 引 言

在复杂的交通路网中，找到一条到目的地合适的行车路径是智能交通系统的重要组成部分。更好的道路规划可以缓解交通拥堵，缓解城市交通压力，方便人们出行。行车路径规划问题也是城市智能交通的重要组成部分[1-2]。它是一种行程路径的设计与优化。现有资源再利用与配置的基础是智能停车引导系统的重要研究内容。行车路径的设计是引导车辆参考实时路况问题设计的最佳行车路线，减少驾驶者在道路上的代价消耗。合理的行车路径，一方面可以避免因路况不熟悉而造成停车使用者迷路的情况，减少车辆在复杂路网中的交通时长，优化交通流在道路网络中的分布，另一方面可以减少停车使用者因长时间找不到停车位，而选择路边非法停车，在一定程度上提高了交通安全[3-4]。

现代启发式算法中的遗传算法和蚁群算法都属于仿生学算法，两种算法对于求最短路径问题都有一定的优势，并取得了一定的成果。但同时两种算法在设计时都有各自的缺点，遗传算法通过不停的迭代进化却没有利用反馈信息，导致冗余迭代，降低了求解效率。而蚁群算法由于在初期信息素匮乏，导致算法速度慢[5-6]。通过将两种算法相结合，提取两种算法的优点，可以加快算法的迭代速度，提高求解效率。

目前，利用仿生学遗传-蚁群算法解决路径优化问题已经取得了一定的成果[7-9]。针对两种算法的优化问题，国内外很多学者对这两种算法进行改进。例如，文献[7]提出基于云模型的蚁群算法，文献[8]提出多工种蚂蚁分工的蚁群算法，文献[9]提出将蚁群算法与遗传算法中的变异因子结合，对遗传算法中的交叉长度的变化和蚁群算法中的信息素保留率进行改进。但改进的算法同样存在较多问题，如陷入局部解、收敛速度慢、求解精度低等。因此，文中从基本蚁群算法入手，结合遗传和蚁群算法的各自优点，将两种算法的寻优过程循环多次。在蚁群算法的每一次循环迭代后，将蚁群算法产生的最优解加入到遗传算法中，用以加快遗传算法的迭代速度。同时，将遗传算法算出的解设为较优路径来更新蚁群算法中的信息素分配，实现参数调整。多次相互指导能有效解决蚁群算法前期效率低和遗传算法后期冗余迭代的问题。实验结果表明，GACHA算法可以有效地避开局部较优解，加快算法迭代速度，提高求解效率。它具有良好的收敛性和求解效率并且能在复杂路网中找到合适条件的最短路径。

1 算法原理

1.1 基本遗传算法

遗传算法是由达尔文的进化论思想衍生出来的仿生学最优化算法，通过适应度函数对较优个体进行不断选择的过程。同时为保持种群的多样性和具有求全局最优解的能力，较优个体需进行交叉和变异操作产生新的种群。通过不断的选择和迭代进化，找到最优个体，也就是最优解[10-11]。

1.1.1 编 码

编码是将实际求解问题的实际参数通过编码变成遗传算法中的基因码组。在实际操作中为操作方便，经常转换成二进制基因码，通过0或1便是表示个体具体的某一个变量值。一个个体是一个二进制字符串，字符串长度由求解的精度决定。

1.1.2 确定适应度函数

设计适应度函数的目的是计算和评价每个个体在当前环境中的适应度值，然后决定该个体是被保留还是被放弃。目标函数f(x)被设置为适应度函数。个体的适应值越小，个体的素质越好。

1.1.3 交叉操作

通过将父系中剩余的染色体配对，一对配对的染色体被交叉并以交叉概率PC重组以产生后代个体。改进的两点交叉方法可以在一定程度上提高种群的多样性。

1.1.4 变异操作

变异操作是指从进化的种群个体中选择部分，然后改变个体基因码即二进制字符串的部分顺序，或者使基因码部分发生交换“突变”，以保持种群多样性，防止算法过早收敛。

1.2 基本蚁群算法

蚁群算法(ant colony optimization，ACO)是通过观察蚂蚁觅食路径选择过程而启发的路径优化算法。它源于真实蚂蚁在寻找食物时相互协作，通过信息素的调节，给后面的蚂蚁以指导启发，而得出最优路径问题。蚁群算法通过信息素的调节和转移，可以保持种群的多样性，优化全局寻优能力[12-13]。

蚁群算法是一种启发式仿生学算法，在蚂蚁觅食过程中，蚁群通过相互间的协助总能够寻找到一条从蚁巢和食物源的最优路径。图1显示了这样一个觅食的过程。

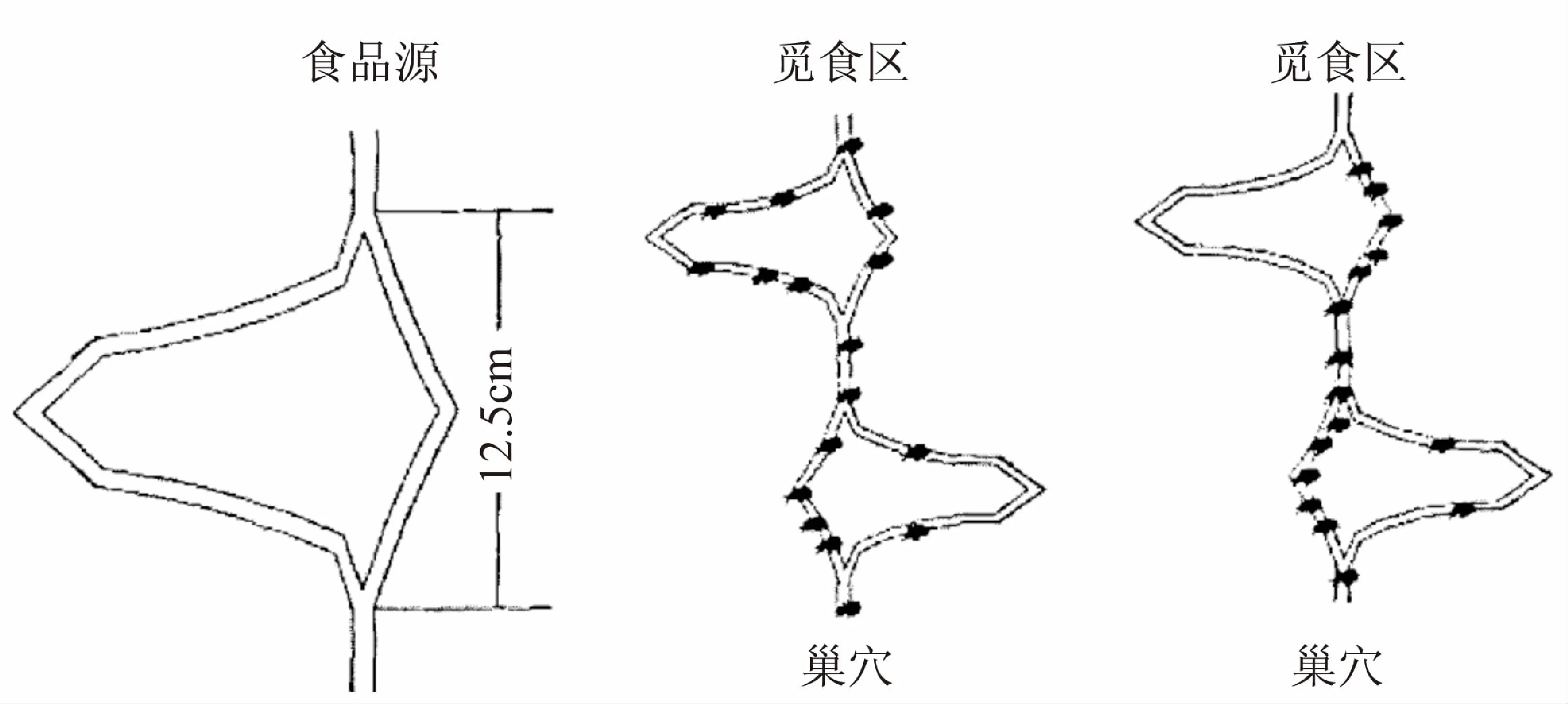
图1 蚂蚁觅食

在图1中，当蚂蚁发现一个食物源时，蚂蚁们从巢穴沿着一条直线向食物源行走，并沿着这条线返回。如果在巢穴和食物源之间突然出现另一条道路，则蚂蚁去食物源的路上将有一个岔路口，蚂蚁需要选择是向左边行驶还是向右边行驶。在最开始不知道的情况下，蚂蚁随机选择，概率相等，所以两条路的蚂蚁几乎一样多。蚂蚁走过会留下信息素用于指导后面的蚂蚁行驶，随着时间的推移，上边路段相同时间经过的蚂蚁会多一些，会留下更浓的信息素，指导这后面的蚂蚁行驶，如此形成正反馈，从而吸引更多的蚂蚁沿着这条路行驶。

蚁群算法遵循的规则：

(1)感知范围：蚂蚁只能观察到其周围一个方形区域，模拟相关参数为速度半径r，可观察和移动的范围为r×r区域。

(2)环境指导：行走的路径上可能会有障碍物或者其他蚂蚁的信息素，信息素以一定速度进行挥发。

(3)食物刺激：在周围寻找食物过程中，当食物源出现在其感知范围内，就会发现食物，否则，沿着信息素的概率比选择行驶路径，即使信息素很少仍然有较低的概率会选择，巢穴信息素指导规则相同。

(4)行动准则：蚂蚁按照信息素的比例向信息素浓度高的路径行走，信息素浓度小的路径也有小概率被行走，当完全没有信息素时按原有方向行走并记录当前位置。

(5)避开障碍：当蚂蚁行走过程遇到障碍，起初按随机概率选择前行，并留下信息素，当有信息素指引时，将按照觅食规则移动。

1.2.1 状态转移规则

状态转移规则是选择下一节点的标准。下一个节点的选择取决于两节点之间的距离和之间信息素浓度的大小。状态转移概率表示为：

(1)

其中，α表示信息素启发式因子，β表示期望值启发式因子，allowedk={0,1,…,n-1}表示蚂蚁下一步允许选择的节点，τα(i,j) 表示存储在路段L(i,j)上的信息素浓度，ηβ(i,j)表示节点i到节点j的可见度,通常取值为节点i和节点j之间距离的倒数。

1.2.2 信息素更新

当蚂蚁寻找到一条路径时，需完成对这条路径信息素的更新，之后对所经过路径上的信息素浓度进行全局更新，以确保选择最优路径的概率增加，信息素更新规则如下:

τij(t+n)=(1-ρ)τij(t)+Δτij(t)

(2)

(3)

其中，ρ∈(0，1)为蚂蚁信息素的挥发系数，τij(t+n)为(t+n)时刻路径上信息素的浓度，Δτij(t)为本次循环中最优路径上的信息素增量，Lk为本次觅食过程中蚂蚁k所走的路径长度，Q为蚂蚁k路径过程中总的信息素量，m为此次循环蚂蚁数量。

2 混合算法

2.1 混合的基本思想

经过专家和学者们对遗传和蚁群算法进行的大量实验表明，遗传算法与蚁群算法的总体进化迭代曲线如图2所示。

图2 速度-时间曲线

从图2中可以看出，遗传算法在搜索的初期(T0-Tb区间段)具有较快的向最优解靠近的进化速度，在Tc之后进化迭代速度明显下降，在到达Tg时刻之后，其开始落后于蚁群算法。相比较于遗传算法，蚁群算法由于在搜索的初期(T0-Tb区间段)信息素较少且分布平均，导致算法进化速度缓慢。随着各条线路信息素的积累，Td时刻后，蚁群算法的收敛速度开始迅速增加。通过分析,遗传算法前期虽然具有快速的全局搜索能力，但是没有反馈信息，导致后期的冗余迭代，降低了算法的求解效率。蚁群算法通过信息素的反馈，进行启发式的指导，具有更好的收敛能力。但是由于前期信息素少且分布较为平均，导致前期运算缓慢[14]。

因此通过将遗传算法和蚁群算法相结合，其主要目的是结合两种算法的优势，去除两种算法的不足，实现优势互补。为此,可以在算法多次循环迭代中，循环结合，相互指导。在蚁群算法的每一次循环迭代后，将蚁群算法产生的最优解加入到遗传算法中，用以加快遗传算法的迭代速度。同时，将遗传算法算出的解设为较优路径来更新蚁群算法中的信息素分配，实现参数调整。多次相互指导能有效解决蚁群算法前期效率低和遗传算法后期冗余迭代的问题。

遗传算法与蚁群算法相结合的优点是，当遗传算法达到一定的搜索阶段时，可以克服搜索最优解的效率低下和蚁群算法初始信息素的不足[11-13]。同时，也可以充分发挥各自的优势，寻找最佳解决方案，弥补彼此的不足。

2.2 混合算法的步骤

2.2.1 算法参数初始设置

设置算法的初始化参数，包括遗传算法的交叉概率Pc和异变概率Pm，蚂蚁的数量m，蚂蚁信息素的启发因子及期望值启发因子。

2.2.2 更新遗传种群，找出较优个体进行编码

根据适应度函数计算每一个个体的适应度，然后通过概率大小选择较优的个体。假设种群大小为m，父代种群Z={a1,a2,…,am},其中每个个体的适应度大小为f(ai)，子代群体初始状态为x=0,则具体操作过程如下:

步骤1:将所有个体按其适应度值由大到小进行排序，排序后的种群为Z'={b1,…,bi,…,bm}，其中f(bi-1)>f(bi)>f(bi+1)。

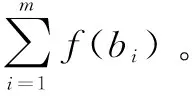
步骤3:计算出每一个个体被选取的概率:

之后对较优个体进行编码，给每一个节点一个序号，从起点到终点的一组序号列为一组编码。

2.2.3 交叉操作

系统随机产生0到1之间的浮点数，当该数小于交叉概率Pc时(一般取值0.6～0.8)，执行交叉操作。通过将父系中的基因码进行配对，两个基因码通过交叉后再重组以产生后代个体。假设父代基因码1-13-14-15-21-20-25-26-31-29-30和1-2-12-15-21-20-25-26-31-29-30随机选取片段如14-15-21片段进行交叉得到1-13-12-15-21-20-25-26-31-29-30和1-2-14-15-2-20-25-26-31-29-30两个后代。交叉操作可以在种群中添加未有却又相近的基因，从而提高种群的多样性。

2.2.4 异变操作

系统随机产生0到1之间的浮点数，当该数小于异变概率Pm时(一般取值0～0.2)，执行异变操作。通过交叉操作产生一个新基因码后，需要在基因码中随机选择若干个基因片段，然后随机修改基因的值，从而给现有的染色体引入了新的基因，突破了当前搜索的限制，更有利于算法寻找到全局最优解。

2.2.5 遗传循环操作

统计遗传算法的迭代次数，如果达到设定的最大次数则终止循环，输出若干组遗传算法较优解。否则，继续迭代循环返回步骤2.2.2更新遗传种群操作。

2.2.6 根据已知较优解分布信息素

初始各路径上的蚂蚁信息素浓度为一个常数，根据遗传算法的较优解作为初始解，通过这些较优解，调节并更新这些解的蚂蚁路径信息素分配，根据式(2)局部更新每条路径上的信息量。

2.2.7 蚁群寻路操作

将m只蚂蚁放在起点位置，从当前位置i到下一节j的选择概率根据状态转移规则概率分布进行选择。同时更新禁忌表、允许访问的节点列表和未访问的节点列表。若当前节点为终节点，则完成以此寻路过程的循环，否则继续下一节点的选择，直到m只蚂蚁完成寻路过程，同时更新路径信息素。

2.2.8 蚁群循环操作

统计蚁群算法的迭代次数，如果达到设定的次数则终止循环，输出蚁群算法若干较优解。否则，继续迭代循环，返回步骤2.2.6分布信息素操作。

2.2.9 系统循环过程

统计系统循环次数，若达到设定的最大迭代次数或者达到寻优条件，则输出全局较优解为问题最优解。否则，返回步骤2.2.2更新遗传种群操作，将蚁群算法的较优解作为精英个体加入到遗传算法群体中。

3 实验结果及分析

本仿真数据采用某市部分地图的路网信息，路网结构如图3所示，其中双向线表示城市道路。

图3 某市路网结构

路网包含的数据信息见图4，其中i、j表示路网的节点，dij为相邻节点间路段的实际距离，由于路段是双向行驶且距离基本相同，即dij=dji；tij为i、j节点的道路拥堵情况等级。

i1122334455789j213123411510788910dij550300370480450420530470460310400410650tij1123141235512

i9101011111212131414151516j18111712161315141522162117dij560510570440600470600590450970450880510tij2331213212322

ii17171819192020212122232324jj18201920272125222423243425dijdij630760700590610930590540600560580490890tijtij1234221445312

ii24252626272929292830323233jj33262731292830313032313334dijdij5203201505305601801501503003301801100600tijtij2211245122221

图4 路网包含的数据信息

将文中算法用于静态路网所得的初始路径规划结果如图5所示。

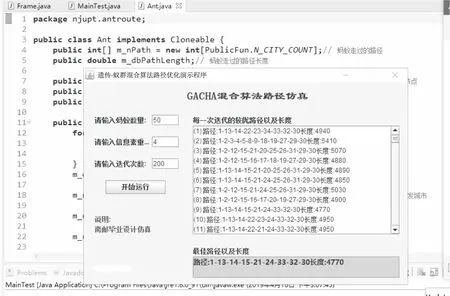
图5 静态路网下最优停车路径仿真结果

算法在静态路网下20次的效果对比如表1所示。

表1 几种算法在静态路网下20次的效果对比

在动态路网模型中，还需要提供路段上的实际交通拥堵状况从而获取动态路权。此实验中给道路拥堵情况分为五个等级，道路实际权值Lij=dij*tij是本实验提供的与初始路线相关的部分路段的动态拥挤度，用于动态路网的仿真实验。

结果见表2和图6。

表2 几种算法在动态网路下20次的效果对比

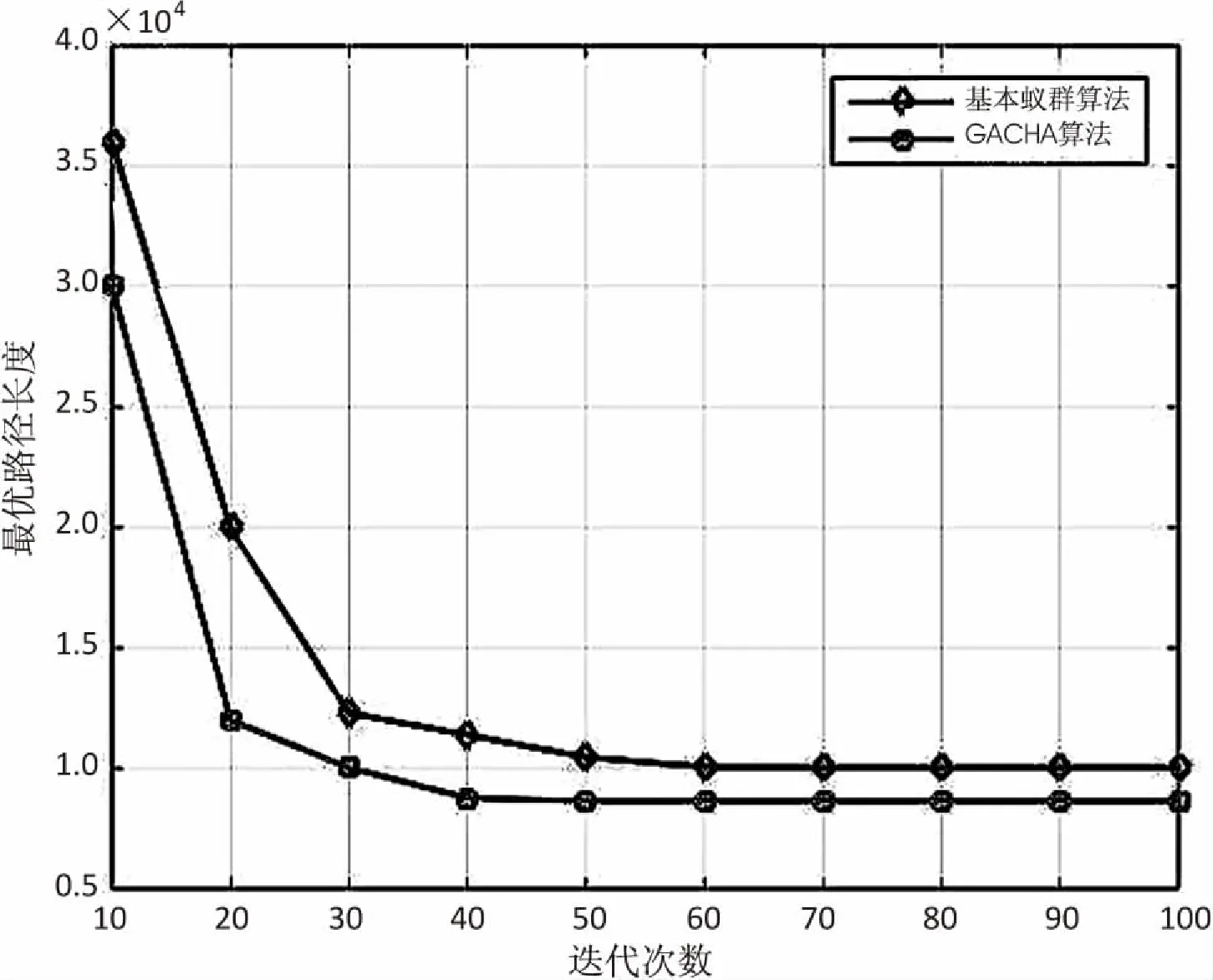
图6 实验最优解进化曲线

4结束语

首先对基本蚁群算法和遗传算法的原理、流程和步骤做了详细介绍，分析了仿生学算法在解决复杂路网下的最优路径问题的优越性。结合遗传、蚁群算法的特性和优点，设计一种混合遗传蚁群算法(GACHA)用于系统的路径规划中。从基本蚁群算法入手,将两种算法的寻优过程循环多次结合。在蚁群算法的一次迭代循环后，将蚁群算法产生的较优解代替遗传算法中的部分个体，用以加快遗传算法的迭代速度。同时，将遗传算法算出的解设为较优路径来更新蚁群算法中的信息素分配，实现参数调整。多次相互指导能有效解决蚁群算法前期效率低和遗传算法后期冗余迭代的问题。实验结果表明，GACHA算法具有良好的优化和收敛性，能够准确地找到满足路网综合要求的最优路径。