基于演化博弈的蜜罐有效性机理证明
2020-04-30赵俊楠石乐义
李 阳,赵俊楠,石乐义
(中国石油大学(华东) 计算机与通信工程学院,山东 青岛 266580)
0 引 言
随着近年来信息技术的迅速发展,计算机网络已渗透到社会工作生活的方方面面,网络安全日益受到重视并成为国家战略安全的一部分,网络攻防博弈日趋激烈。然而,传统的防御手段如防火墙、入侵检测技术等大都属于静态、固定、敌暗我明的被动防御,对于网络对抗尤为不利。在此背景下,蜜罐技术应运而生。蜜罐技术是一种网络诱骗[1]陷阱,其目的在于迷惑攻击者,研究学习攻击行为和目的,追踪监视攻击者,从而保护信息系统安全。
攻防双方作为蜜罐防护过程的参与者,策略相互依存,并根据敌手不同情况选择最佳响应策略,因而构成了博弈推理基础条件。作为一门使用严谨数学模型研究现实世界冲突对抗条件下最优决策问题的理论,博弈论可通过建模分析,对网络性能优化、安全技术有效性证明等问题进行研究[2-3]。文中旨在将演化博弈应用于网络安全领域,对蜜罐技术进行演化博弈建模,分析网络中各参与者之间的均衡策略和演变过程,对网络安全优化部署提出有效建议。
1 国内外研究现状
蜜罐作为一种主动防御手段,通过模拟真实网络环境,诱骗攻击者并分析其在蜜罐中的恶意行为。文献[4]将网络诱骗攻防视为多阶段信令博弈,对蜜罐诱骗性能进行研究;文献[5]利用不完全信息博弈,构建蜜罐攻防博弈模型;文献[6]提出基于蜜网诱骗模型的博弈理论框架,分析均衡解;文献[7]将蜜罐诱骗系统与不完全信息动态博弈结合,提出基于模糊矩阵博弈的网络安全威胁评估。Hayatle O[8]提出基于贝叶斯博弈的理论框架,模拟了蜜罐与僵尸主机控制方之间的零和非合作博弈,使防御方采取最佳响应策略;Wagener G[9]利用博弈理论改善蜜罐的自适应特性,使蜜罐改变交互行为特征,以获取更多攻击信息;Wei L[10]将蜜罐信息融合阶段视作博弈过程,集成博弈理论与信息融合技术,获知最佳安全防御决策。
孙庆文等人借鉴生物进化过程中“复制动态”思想,对非对称2×2演化博弈均衡进行渐近稳定性分析[11],并简要讨论了演化博弈框架下经济行为模式动力学意义。文献[12]从网络攻防对抗的实际情况出发,在有限理性约束下,构建非合作攻防演化博弈模型并提出最优防御策略选取算法,进而推测演化规律。张恒巍等人[13]根据攻防过程中的动态变换特征和有限理性约束条件,利用Markov多阶段攻防演化博弈模型,分析单阶段演化模型,引入贴现因子、计算折扣收益,以动态规划法求解多阶段演化均衡策略。黄健明等人[14]利用激励系数,构建基于改进复制动态攻防演化博弈模型。通过雅克比矩阵中局部稳定分析法,实现均衡点稳定性分析,获取不同情形下的最优防御策略。付世华[15]利用矩阵半张量积方法建立代数表达,研究具备破产风险和多步记忆的网络演化博弈策略优化问题,并分析时变拓扑结构下具有多步记忆的网络演化博弈稳定性。Yin Y等[16]提出了防火墙与入侵检测系统之间相互作用的博弈论模型。论文将演化博弈论引入至安全系统主动保护机制研究,认为博弈论模型行为主体是由多个参与者组成的有界理性群体。通过所提出的利润矩阵建立成本效益设置模式。在网络安全系统设备主动策略移动中考虑响应代价因素,具有很大实用价值。Huang K等人提出一种基于演化博弈机制的物理层安全协作方法[17],根据演化博弈机制定义策略(噪声/正常信号)和收益(不同安全速率);发送端通过连续调整策略使演化达到稳定状态,然后动态调整,使网络从不稳定状态向协作稳定状态演变,从而提高整个系统的安全速率。文中基于演化博弈理论,将网络服务器端视作一种简单生态环境,可为不同来访者提供服务资源,且不同来访者为环境中生存的不同种群,每个种群在网络中具备各自行为方式。通过研究混合网络系统(蜜罐诱骗系统与正常服务系统)和攻击者之间的均衡博弈策略演变,证明在网络中部署蜜罐是一种主动且有效的防御方式。
2 演化博弈
2.1 演化博弈概述
在现实社会,每次博弈情景可能极其复杂,且推理出均衡战略结果需要复杂且漫长的步骤过程。所以社会学家们逐渐从生物学中推导出一种新规则,一类根据社会演变总结出的规律——演化博弈理论。
演化博弈论(evolutionary game theory)强调一种动态均衡,从一种全新角度诠释了博弈均衡概念,不再是完全理性也非完全信息,为纳什均衡和均衡战略的选择演绎出新方法。其中最重要的概念是演化稳定策略(evolutionary stable strategy),指如果占群体绝大多数的个体选择演化稳定策略,那么小突变者群体就不可能侵入到这个群体。
2.2 演化稳定策略
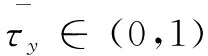
即一种演化稳定策略需要同时满足以下条件:对任意策略y≠x,具备
(1)均衡性,u(x,x)≥u(y,x)。
(2)稳定性,u(x,x)=u(y,x)⟹u(x,y)>u(y,y)。
条件(1)保证了策略x满足纳什均衡,如果参与者任意改变策略,自身利益将无法达到最大化。当少部分变异者入侵种群时,只有采用策略x是其最优选择,变异才会被逐渐淘汰。若存在其他最优策略y,只有保证策略x更优于y,才能使种群突变难以继续存活下去。
定理1:如果策略集(x,x)满足严格纳什均衡,那么策略x是演化稳定策略。
定理2:在双人对称博弈中,参与者的策略集合中只有策略x和策略y,且支付函数满足u(x,x)≠u(y,x),u(x,y)≠u(y,y),那么该博弈存在演化稳定策略。
演化稳定均衡分为单元均衡和多元均衡。单元均衡是指将一个环境中所有参与者视为一个群体,参与者行为是一个特定纯策略集合,种群中仅存在一种战略。否则,称之为多元均衡。
2.3 复制动态方程
演化博弈是一个种群为了适应环境存活而不断进行演化最终达到稳定状态的过程,其演化机制包括选择机制和突变机制。选择机制指某一个策略在某次博弈中可通过获得较高收益使参与者在之后博弈中更倾向于选择该策略作为博弈首选,力求达到自身收益最大化;突变机制则是博弈参与者随机选取某一个收益未知的策略进行冒险博弈,因而并不常用。演化博弈是根据收益最大化理论,博弈参与者频繁采用收益高于平均水平的策略集,因而博弈群体中各种策略集使用比例有所不同。
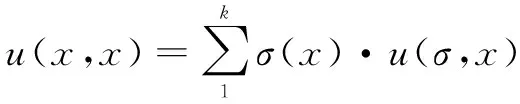
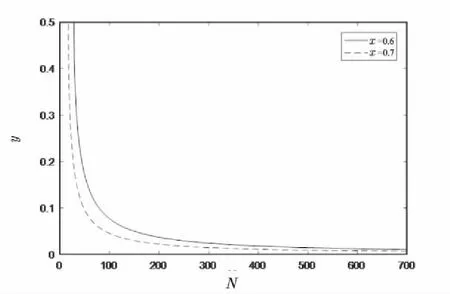
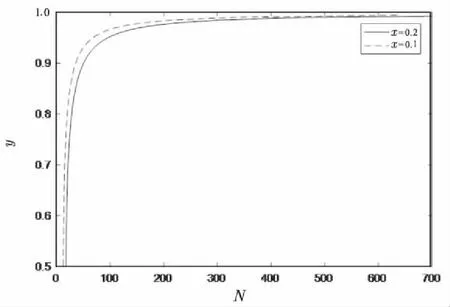
从上述复制动态方程中可看出,当u(x,σ)>u(x,x)时,选择策略x的参与者获得的收益大于平均值,那么选择策略x的子群体会扩大规模;u(x,σ) 将网络系统视为演化博弈中的生态环境,所有访问网络的来访者视为环境中的不同种群。网络系统以概率x部署蜜罐以概率1-x不部署蜜罐系统,当访问网络的来访者仅有攻击者一个“种群”时,攻击者可以选择以概率y访问网络或者以概率1-y不访问系统。博弈收益矩阵如表1所示。 表1 演化博弈收益矩阵 为简化收益矩阵,文中默认攻击者访问蜜罐系统成功率为100%,且攻击者攻击普通系统收益和系统被攻击损失相等。推理参数设置Np为网络系统正常服务收益,Nc为网络中蜜罐部署成本,Ap为攻击者攻击收益,Ac为攻击者攻击成本。 (1)针对网络系统。 选择策略“蜜罐系统”的收益为: u1=y·(Np-Nc-Ap)+(1-y)·(Np-Nc) 选择策略“普通系统”的收益为: u2=y·(-Ac)+(1-y)·Np 网络系统的平均收益为: u=x·u1+(1-x)u2=Np-xNc-Npy-Apy+Npxy 网络系统的复制动态方程为: F(x)=dx/dt=x[u1-u]=x(1-x)(Npy-Nc) 图1 函数F(x)的变化趋势 函数F(x)的变化趋势可以反映策略“蜜罐系统/普通系统”随着时间推移的演化过程。 令F(x)=0,可得三个值:x=0,x=1,y=Nc/Np。根据前述理论知识可知,演化博弈的稳定策略就是复制动态曲线与水平坐标轴相交且交点处切线斜率为负数的点,函数F(x)化趋势如图1所示。 当y>Nc/Np时,交点x=0处的切线斜率为正,交点x=1处的切线斜率为负,所以只有x=1是网络系统演化稳定策略,即网络系统最后会选择部署蜜罐系统这一策略。当y 当y=Nc/Np时,函数F(x)无变化趋势,网络系统与攻击者的演化博弈不存在演化博弈稳定策略。 (2)针对攻击者。 选择策略“访问”的收益为: 选择策略“不访问”的收益为:u4=0 平均收益为: u'=y·u1+(1-y)u2=Apy-Acy-Apxy 复制动态方程为: F(y)=dy/dt=y[u3-u']=y(1-y)(Ap-Ac-Apx),函数F(y)变化趋势可以反映策略“访问/不访问”随着时间推移的演化过程。 令F(y)=0,可得三个值:y=0,y=1,x=Ap-Ac/Ap。根据前述理论知识可知,演化博弈的稳定策略就是复制动态曲线与水平坐标轴相交且交点处切线斜率为负数的点,函数F(y)的变化趋势如图2所示。 图2 函数F(y)的变化趋势 当x>Ap-Ac/Ap时,交点y=0处的切线斜率为负,交点y=1处的切线斜率为正,所以只有y=0是攻击者的演化稳定策略,即攻击者最后会选择访问网络系统这一策略。当x 当x=Ap-Ac/Ap时,函数F(y)无变化趋势,网络系统不存在演化博弈稳定策略。 对于小学生来说,英语学习的确具有一定的难度。这不同于自己的母语,在学习的过程中,学生会感到很多内容都是全新的,需要他们付出大量的时间和精力来把这些内容掌握住。因此如果教师不采用有趣的教学方式来组织教学活动,就可能让学生在困难面前表现出退缩的状态。在教学实践中,我们发现多媒体以及实物教学等形式可以更好的引导学生进入一种更加投入的学习状态中,从而有效提高他们的兴趣,也提高了他们学习的成效。 令复制动态方程F(x)=0,F(y)=0。可得演化博弈的五个均衡点(0,0),(1,0),(0,1),(1,1),(Ap-Ac/Ap,Nc/Np)。每一个均衡点都是一个满足纳什均衡条件的策略组合。描述网络系统和攻击者的复制动态关系如图3所示。 图3 网络系统和攻击者的复制动态关系 由图可知,演化均衡点(1,0)和(0,1)是网络系统与攻击者双方博弈的最终演化稳定方向。当网络系统与攻击者的策略组合属于区域A时,演化会向均衡(0,1)收敛,即若网络系统为普通系统,攻击者会选择访问系统;当网络系统与攻击者的策略组合属于区域B时,演化会向均衡(1,0)收敛,即若网络系统为蜜罐系统,攻击者会选择不访问系统,显然该结论符合现实情况。均衡点(Ap-Ac/Ap,Nc/Np)是影响演变方向的阈值,当网络系统和攻击者的策略组合在均衡点(Ap-Ac/Ap,Nc/Np)时,一个极小的改变会决定演化最终走向,所以在演化博弈中,博弈参与者行动不断变化,博弈双方都会向适应自身发展的方向进行演变,如图中的区域C、D。当网络系统和攻击者的策略组合属于这两部分时,演化具有一个不确定性,即可能由C→A→(0,1),也可能由C→B→(1,0)。这与实际情况有关,如果在网络系统中部署蜜罐代价很大,管理人员可能放弃部署;如果访问蜜罐对攻击者造成的损失很严重,攻击者可能会放弃访问一个不确定的系统。 通过Matlab对上述演化推理进行验证,分析引入蜜罐策略后对攻击者访问策略造成的影响。设参数Np=1,Nc=0.4,部署概率x的初始值为0.5,阈值y=Nc/Np=0.4。 (1)当y>0.4时,取y=0.6,y=0.7,仿真结果如图4所示,x最终收敛至x=1。即当攻击者攻击概率较大时,无论访问概率怎样变化,网络系统最终的选择策略都是部署蜜罐系统。 图4 仿真结果(y=0.6,y=0.7) 图5 仿真结果(y=0.3,y=0.5) (2)当y=0.4时,取y=0.3,y=0.5,结果如图5所示,系统处于不断变化状态。任何微小改动将导致均衡向不同方向演化,符合前文区域B、D的情况。 (3)当y<0.4时,取y=0.1,y=0.2,仿真结果如图6所示,x最终收敛至x=0。即当攻击者攻击概率较小时,无论访问概率怎样变化,网络系统的最终选择策略都是不部署蜜罐系统。 图6 仿真结果(y=0.1,y=0.2) 设参数Ap=0.9,Ac=0.5,部署概率y的初始值为0.5。阈值x=Ap-Ac/Ap=0.44。 (4)当x>0.44时,取x=0.6,x=0.7,如图7所示,y最终收敛至y=0。即当系统部署蜜罐的概率较大时,攻击者最终的选择策略都是不访问系统。 图7 仿真结果(x=0.6,x=0.7) (5)当x<0.44时,取x=0.1,x=0.2,如图8所示,y最终收敛至y=1。即当系统部署蜜罐的概率较小时,攻击者最终的选择策略是访问系统。可知,对蜜罐系统比重的增加,会使攻击难度加大,攻击者攻击成本也会相应增加。管理员也可不断对蜜罐系统进行升级,使其诱骗性能不断加强,从而使蜜罐具有更好的迷惑性和实用性。在网络中部署蜜罐系统会提升网络安全性能,通过诱骗和伪装给非法攻击者带来巨大损失,一旦攻击者的攻击消耗资源大于其所得,便有可能吓退攻击者使其放弃访问网络系统。 图8 仿真结果(x=0.1,x=0.2) 文中将设置蜜罐系统的混合系统看作生态环境,来访者仅为攻击者一个种群,通过演化博弈观察分析混合系统和攻击者在网络中的演变过程,证明蜜罐有效性。主要通过演化博弈理论对网络系统中所部署蜜罐的有效性进行证明,从理论推导到仿真验证,讨论了两个参与者——网络系统和攻击者在竞争过程中的演变均衡策略,证明了通过优化蜜罐可以达到迫使攻击者放弃访问系统的目的。3 建模与仿真
3.1 蜜罐诱骗系统中的演化模型
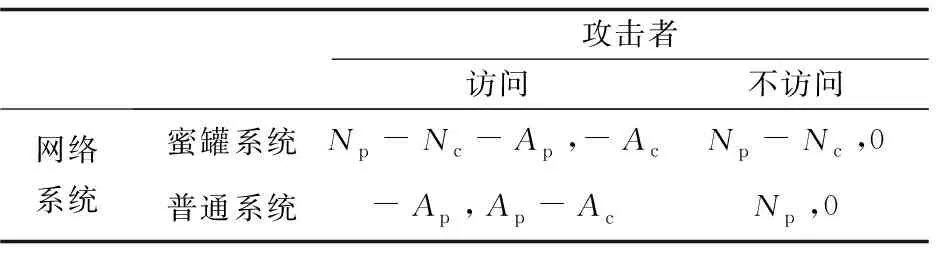
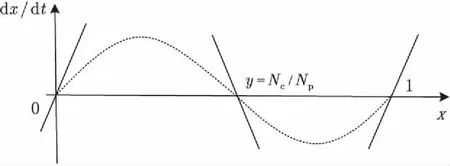
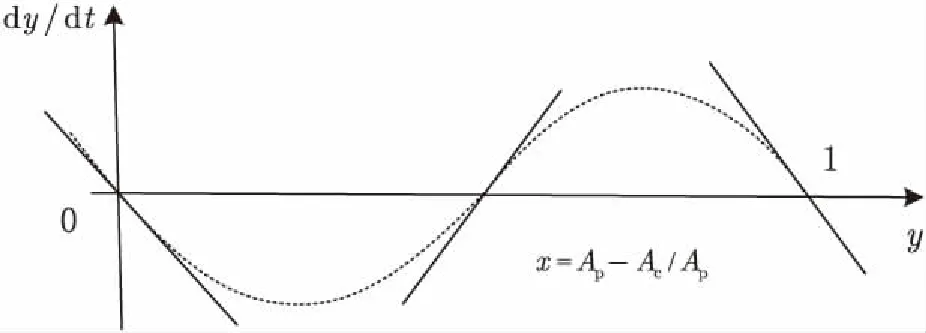

3.2 仿真验证
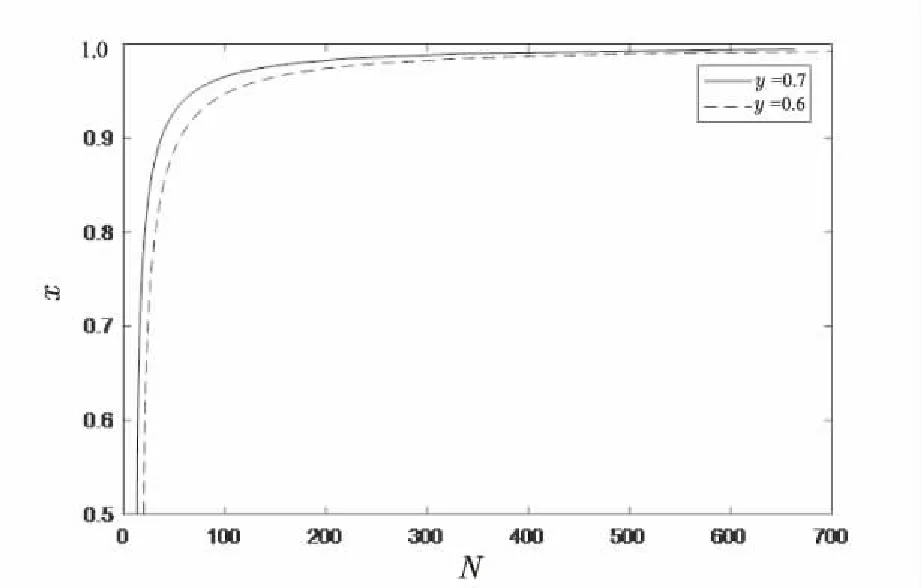
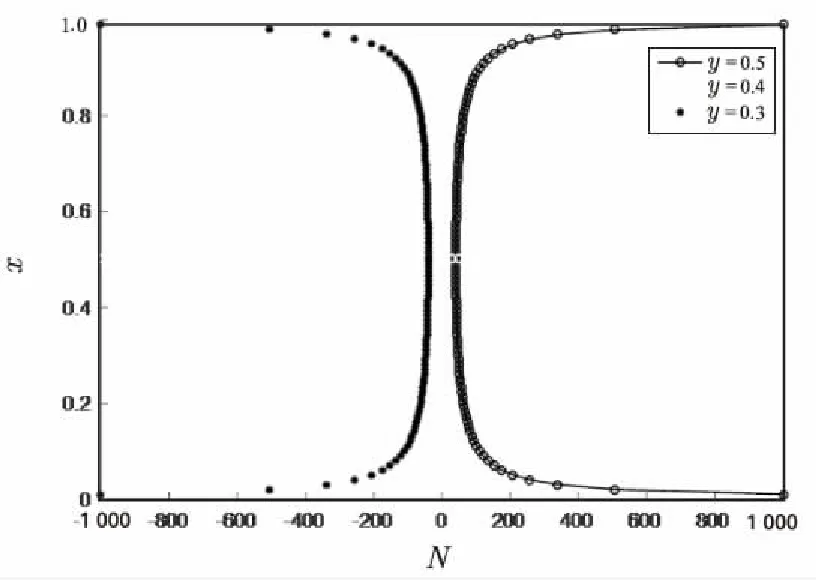
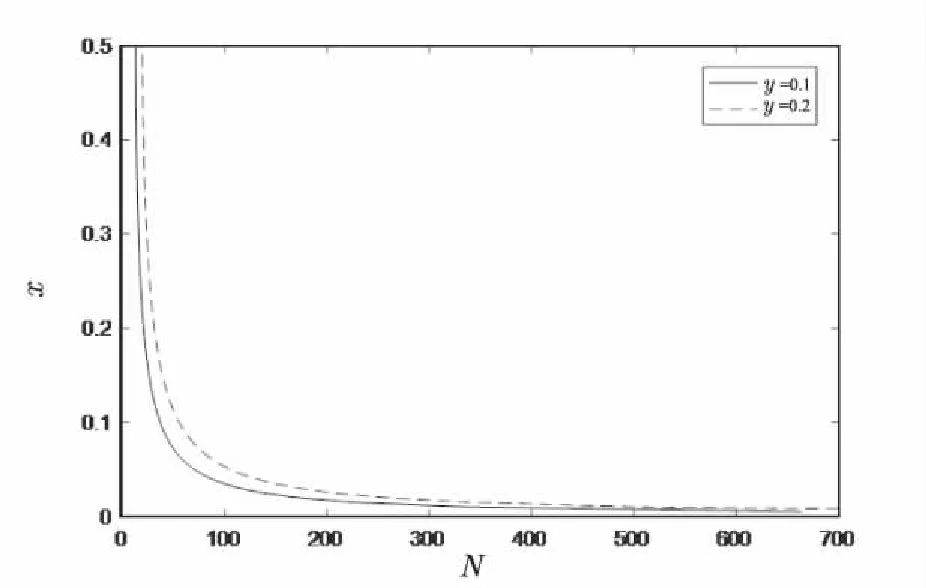
4 结束语
