基于头脑风暴算法的电动货车路径优化问题

齐元豪，王 凯，付亚平

(青岛大学 电气工程学院，山东 青岛 266000)

0 引 言

近年来，关于电动汽车在物流领域的研究越来越多[1-2]。但关于电动汽车路径问题、物流网络智能调度的研究却不多。Sawik等人[3]提出了一种使噪声，污染和成本最小化的路径模型。梁凤婷等人[4]以低碳、节能和低成本为目标，分别对传统汽车和电动汽车的路径模型进行对比分析。郭戈等人[5]从充电、路径和车队配置等角度,着重介绍了3种路径优化分支。金仙力等人[6]提出了一种基于遗传算法的路径优化算法,用以解决带时间约束条件的车辆路径问题。Muratori等人[7]提出了一种描述电动汽车电池能耗的模型。Zhou等人[8]提出了一种电动汽车路径选择和充电站位置分布的模型。Zeng等人[9]提出了一种基于随机地形来进行电量管理的策略。Wang等人[10]对电动汽车与传统汽车进行了分析对比。

由于市场需求的不断扩大，物流配送中心车辆资源的有限性，因而在车辆资源与市场之间存在时间和配送服务上的矛盾与冲突。如何有效分配物流车辆以及提高服务质量一直是车辆调度问题的关键[11-12]。为此，在这些成果的基础上，文中研究了带有时间窗的电动货车路径优化问题(EVRPTW)，以电动货车耗电量、顾客满意度为目的建立数学模型，以此来对物流中心的车辆调度任务进行有效管理和合理分配有限的电动货车资源。同时，将人工智能方法引入此物流网络的智能调度中，利用智能算法、调度经验等来求解最优解，形成合理有效的调度方案。

1 问题描述

文中研究的问题属于带时间窗有容量的电动汽车路径优化问题(electric vehicle routing problem with time windows，EVRPTW)。此问题可描述为，现有一物流配送中心，电动货车不唯一且为同一类型。要求电动货车满电量从配送中心出发，前往客户点送货，然后回到配送中心。在此过程中，每个客户点只能被一辆电动货车服务且只能服务一次，同时，每个顾客点都有一个时间窗，电动货车无论早到还是晚到都会影响顾客满意度。而电动货车在配送过程允许去充电站充电。该研究的目标是使电动货车在整个配送过程中的总耗电量最小、客户满意度最高。

2 EVRPTW模型

2.1 电动汽车耗电量模型

参考文献[7,13]，电动汽车的电量消耗模型如下：

(1)

(2)

Pin=βPout

(3)

其中，E为所有电动货车从出发到返回过程中消耗的总电量；Pout、Pin分别为电动货车牵引阶段电池电量输出功率、再生制动阶段电池电量输入功率；v(t)为电动货车的行驶速度；M为电动货车的质量；g、fr、α、ρa、CD、Af、δ、β分别为一常数参数，其中，0<β<1。

式(1)为电动汽车行驶过程中的耗电量，由两部分组成，前者为牵引阶段耗电量，后者为制动阶段耗电量；式(2)则为电动汽车牵引阶段耗电功率；式(3)为电动汽车制动阶段耗电功率。

2.2 顾客满意度模型

参考文献[14-15]中关于顾客满意度的描述，文中的顾客满意度模型如下：

(4)

其中，S为顾客满意度；Tje、Tjl、Tjk分别为电动货车k到达j点顾客满意度为0的最早到达时间、最晚到达时间以及实际到达时间。

式(4)为j点顾客的满意度，是由电动货车的到达时间决定的。根据到达时间可分为三部分：早于ej，ej与lj之间，晚于lj，满意度计算公式分别如上式所示。

2.3 EVRPTW模型

模型如下：

(5)

(6)

约束条件如下：

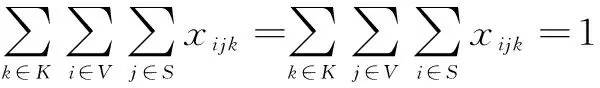
(7)

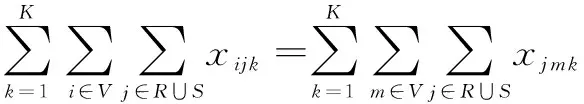
(8)

(9)

(10)

Qmin≤Qjk≤Qmax,j∈V,k∈K

(11)

QOk=Qmax，k∈K

(12)

Wjk=(Wik-wj)xijk,i∈V,j∈V,k∈K

(13)

Wjk≤Wmax,j∈V,k∈K

(14)

tkc+tkp)xijkyik，i∈V,j∈V,k∈K

(15)

tjk=max{Tjk,ej},j∈S∪O,k∈K

(16)

Tik=0,i∈O,k∈K

(17)

(18)

其中，K为电动货车集；O为配货中心；R为充电站点集；S为顾客点集；V为三者集合；Ekij为电动货车k从i点到j点的耗电量；tkp为电动货车k的排队等候时间；Qmax、Qmin、Qjk分别为电动货车的电池容量、最低电量允许值以及实时电量；Wjk为电动货车k在j点的重量；wj为卸货量；Wmax为最大载重量；tijk为行驶时间；vk为卸货速度；tkc为充电时间；yjk、xijk、zj分别为一判定值，若j点为充电站，zj为1，否则为0，若电动货车k在j点充电yjk为1，否则为0，若电动货车k从i到j行驶，xijk为1，否则为0；A为一任意大数值。

式(5)表示整个配送过程中电动货车消耗的总电能；式(6)为整个配送过程中的顾客满意度之和；式(7)确保每个顾客只被一辆车服务；式(8)确保货车路径不重复；式(9)确保电动货车都从配送中心出发最后返回配送中心；式(10)为电动货车在j点时的电量；式(11)为电动货车的电量约束；式(12)表示电动货车满电量出发；式(13)为电动货车j点的载重量；式(14)为电动货车的载重量不能超过自身容量；式(15)为电动货车j点的到达时间，第一项为不充电时到达下一点的时间，第二项为充电时到达下一点的时间；式(16)为电动货车j点开始卸货的时间，最早卸货时间为客户要求的最早到达时间；式(17)表示电动货车从配送中心出发时间为0；式(18)为调用的电动货车数量。

3 头脑风暴算法

头脑风暴(BSO)[16-18]是一种将搜索空间不断缩减的算法。此算法通过不断迭代，最终将局部最优解慢慢精确至全局最优解。其基本过程如图1所示。

图1 头脑风暴算法流程

3.1 种群初始化

随机产生n个个体，每个个体代表一种配送方案。这里应用Matlab仿真软件进行仿真，故个体采用二维编码的方式进行表示。例如，若用数字0表示配送中心，数字1-10表示顾客，数字11-13表示充电站，则个体随机产生的过程可表示如下：首先，得到顾客经过顺序，如[1 2 3 4 5 6 7 8 9 10]；其次，鉴于顾客货物需求以及电动货车容量进行分组，若顾客需求皆为3，电动货车容量为10，则上述顺序可更新为[0 1 2 3 0 4 5 6 0 7 8 9 0 10 0]，每两个数字0之间的数字即为一辆电动货车的配送路线，此顺序即采用了4辆电动货车；再次，根据上述顺序中每辆电动货车的配送顺序求解耗电量、剩余电量，根据剩余电量是否能支撑电动货车到达下一个顾客点最近充电站为判定依据进行充电行为，充电量约束满足式(11)，最高电量为充满，最低电量为刚好到达下一充电站或配送中心。例如[0 1 2 11 3 0 4 5 6 0 7 12 8 9 0 10 0]，此顺序中就表示第一辆与第三辆电动货车需要在配送过程中充电，而此顺序即为个体表示。最后，将个体存放至二维数组中，每一行代表一个个体。

3.2 聚 类

将n个个体进行分类，聚成m个类，分别计算每个个体的适应度值并选出每一类的最优个体作为聚类中心。此适应度值为耗电量与顾客满意度倒数之和，适应度值最小者即为最优个体。耗电量与顾客满意度的求解方式见2.1节、2.2节。

3.3 产生新个体

如公式所示：XNEW=XSELECT+δ(μ，σ)，其中XNEW为新个体，XSELECT为选择的个体，δ(μ，σ)为以μ为均值、σ为方差的高斯随机函数。经过一系列的变异、交叉操作，产生新个体。其中，用于新个体产生公式中的个体选择操作参照图1中的选择过程。通过选择条件P1、P2、P3、P4、P5来决定选择对象，然后根据选择的对象进行交叉、变异操作。该研究中的交叉操作采用两点交叉、变异也采用两点变异。两点交叉即为通过选择操作P5选择的两个对象作为交叉父本，通过设置两个交叉点来进行交叉互换，然后通过映射消除重复位置的因素，最终得到交叉后的个体。例如，现有两个选择对象：[1 2 3 4 5 6]和[6 5 4 3 2 1]，交叉点为第3、第5个位置，那么保持交叉点中间位置不变其余位置互换得到：[6 5 3 4 5 1]和[1 2 4 3 2 6]，经过映射消除得到：[6 2 3 4 5 1]和[1 5 4 3 2 6]，即为交叉后结果。而变异操作则通过对选择操作P4选择的对象进行两点调换。例如，现有一选择对象：[1 2 3 4 5 6]，变异点同样为第3、第5个位置，经过变异操作后为：[1 2 5 4 3 6]。

3.4 更新个体

将新个体与原个体相比较，保留适应度值更好的个体。将每一代的最优个体依次存在二维数组中，每一行代表此迭代的最优结果。

3.5 输出最优解

当达到最大迭代次数后，输出适应度值最优的个体。

4 算例分析

能耗公式中常数参数的取值由参考文献[19-20]确定。图2为应用遗传算法与头脑风暴算法10顾客数，迭代100次的适应度值收敛曲线。其中应用头脑风暴算法得到的收敛曲线相较于遗传算法，适应度值更小，收敛速度更快。具体数值如表1所示。整体来看，无论是采用遗传算法还是头脑风暴算法，在耗电量、顾客满意度以及总目标值方面结果都相差不大，可见该模型的正确性与实用性。具体来看，采用遗传算法的耗电量为286.61，比采用头脑风暴算法的263.69多了22.92；而顾客满意度的导数方面，采用遗传算法的690.78要比头脑风暴算法的724.58少33.8；也就是说采用头脑风暴算法得到的最优解，其耗电量要比遗传算法少，顾客满意度高。可见，该模型采用头脑风暴算法相较于遗传算法具有更好的收敛速度和收敛精度。

为了验证头脑风暴算法的可行性、有效性，文中引入了三个基准测试函数分别对两种算法进行测试。测试结果如表2所示。通过表2可知，对3个基准测试函数的实验中，头脑风暴算法的各项结果都优于遗传算法，具有较好的适应度值、平均值以及较小的标准差。这说明头脑风暴算法具有较好的优化精度和较强的鲁棒性。由此，验证了头脑风暴算法的可行性、有效性。

图2 适应度值收敛曲线

表1 各算法具体适应度值

表2 测试结果

结合对比结果可以得知，该模型能够充分利用电动货车电池容量、顾客时间窗的要求，从而达到降低电动货车耗电量、充电量的效果，进而实现节省配送时间、提高顾客满意度的要求。

5 结束语

探讨了基于头脑风暴算法的电动货车路径优化问题，根据电动货车的耗电量以及顾客满意度提出了一种智能调度方法——EVRPTW模型。通过运用一种计算机智能调度算法——头脑风暴算法，优化配送中心电动货车运营调度问题，从而制定出符合实际情况的运营调度方案。仿真实验验证了该方法的可行性，同时也验证了头脑风暴算法在解决此类问题上的可行性和有效性，进而验证了提出的模型及算法能够节省电动货车耗电量，节省配送时间，提高顾客满意度。但此类问题是在理想情况下进行研究的，忽视了实际问题中的许多随机因素，比如排队充电时间等，这些希望在之后的研究中加以解决。