具有多种吸引子共存类型的新型四维混沌系统

2020-04-29鲜永菊莫运辉徐昌彪吴霞何颖辉

华南理工大学学报（自然科学版） 2020年3期

鲜永菊莫运辉徐昌彪吴霞何颖辉

(1.重庆邮电大学通信与信息工程学院，重庆 400000；2.重庆邮电大学光电工程学院，重庆 400000)

混沌作为一种非常丰富且有趣的复杂非线性现象在经济[1]、神经网络[2- 5]、图像加密[6- 7]、保密通信[8- 9]等领域得到了极大的关注。自Lorenz[10]于1963年发现第1个混沌吸引子以来，许多学者已经构建了许多具有混沌吸引子的新型混沌系统，例如Jerk系统[11- 12]；无平衡混沌系统[13]；分数阶混沌系统[14- 15]等等。

值得注意的是，混沌系统不仅会产生混沌吸引子，而且还会在某些特定参数下产生几个独立的吸引子，即多个共存吸引子。一个典型的例子是著名的Lorenz系统的蝶形吸引子可以分解成两个共存的混沌吸引子或两个共存的极限环[16]。通过深入研究，已发现一些三维混沌系统在特殊参数值下存在共存的吸引子[17- 19]，亦在三维混沌系统的基础上，利用线性和非线性反馈控制构造了具有不同类型吸引子共存的4D和5D混沌系统[20- 28]。例如文献[20]提出的混沌系统在不同参数条件下，具有2个双翼蝶形吸引子共存以及四翼蝶形吸引子。此外，该系统还存在2个双翼蝶形吸引子和4个极限环共存、4个单涡卷吸引子共存、2个双涡卷吸引子和1个极限环共存、4个极限环共存。文献[21]构建了1个具有3个混沌吸引子和1个极限环共存、3个极限环共存、2个混沌吸引子和2个极限环共存的吸引子。文献[22]提出了1个存在不同类型的不对称共存吸引子的混沌系统，其中包括2个周期吸引子共存、1个混沌和1个周期吸引子共存、2个混沌吸引子共存。此外，Prakash等[29]提出了一种特殊的周期性强迫振荡器，它产生无数个共存的嵌套吸引子，包括极限环和混沌吸引子。多个共存的吸引子意味着系统具有多个稳态，通常对系统的性能起着重要影响[30- 32]，比如在不调整参数的情况下能实现不同状态的切换，使系统具有较好的灵活性。

正如许多文献所述，对混沌的研究似乎已经达到了成熟的程度[33- 39]。然而，共存吸引子作为混沌理论的一个新研究方向，仍处于起步阶段。现有文献报道的系统中的吸引子共存类型至多达到6种，本研究提出的系统有10种吸引子共存类型。本研究在文献[21]提出的混沌系统的基础上构造了一个具有多稳定性的新型四维耗散混沌系统，新系统的重要特性体现在：存在10种吸引子共存类型，即4个周期1吸引子共存、2个双涡卷吸引子共存、2个周期1吸引子共存、混沌与拟周期吸引子共存、2个混沌吸引子共存、4个混沌吸引子共存、2个混沌吸引子与2个周期4吸引子、3个混沌吸引子和2个周期1吸引子、2个周期1和2个周期2吸引子共存、4个点吸引子共存；在参数变化b和c改变时，系统频繁地在周期和混沌状态之间切换；随着参数a的变化，系统吸引子形状从单涡卷吸引子到双涡卷吸引子，最后到四涡卷吸引子。

1 系统模型与基本特性

文献[21]提出的混沌系统的状态方程为

(1)

其中，x、y、z、w为系统变量，a、b、c、m为系统参数。将式(1)中第1个方程右边添加线性项-bz，第4个方程的非线性项y2改为线性项-w。可得新型四维混沌系统为

(2)

其中，a∈[0，35]，b∈[-5，3]，c∈[3，8]。对于系统(2)，有

(3)

显然c>0时，系统(2)是耗散的。

平衡点的数量和稳定性对系统的动态行为起着至关重要的影响，多个平衡点的存在亦是产生多涡卷吸引子和多共存吸引子的一个重要因素[40- 41]。为得到系统(2)的平衡点，令式(2)左边为0，即

(4)

可得系统的平衡点为

E0=(0，0，0，0)，

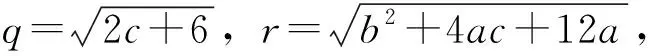
(5)

令det(λI-J)=0，其中，λ表示系统(2)的特征值，I表示单位矩阵，由此得到其特征方程为

f(λ)=λ4+A1λ3+A2λ2+A3λ+A4=0

(6)

对于平衡点E0，A1=a+c-1，A2=-c+ac-a+1，A3=-2c-ac+a-6，A4=-2ac-6a。根据劳斯-赫尔维茨稳定性判据可知，平衡点E0稳定的条件为：

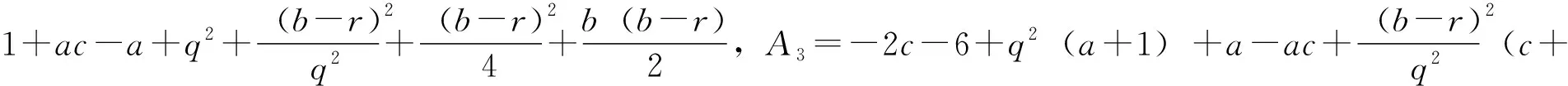
取系统参数a=4.8，b=1，c=5.6，系统(2)的平衡点如下：

E0=(0，0，0，0)，

E1=(4.147，6.945，3.348，-10.044)，

E2=(4.147，-5.945，-2.867，8.601)，

E3=(-4.147，6.945，-3.348，10.044)，

E4=(-4.147，-5.945，2.867，-8.601)。

通过上述稳定条件可知平衡点E0、E1、E2、E3、E4是不稳定的。当初始值为[1，2，3，4]时，通过数值仿真，系统(2)存在一个4涡卷吸引子，如图1所示。此时系统(2)的4个Lyapunov指数(L)为0.120、-0.017、-1.450、-8.053，其Lyapunov维数DL=3+(L1+L2+L3)/|L4|=2.883，从而验证了此吸引子是分形的。

(a)y-z

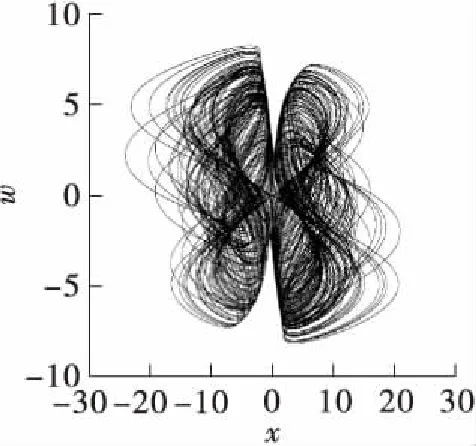
(b)x-w

2 系统参数对系统特性的影响

2.1 参数a对系统特性的影响

取系统参数b=1.0，c=5.6，初始值为[1，2，3，4]。当a∈[0，35]时，系统(2)的Lyapunov指数谱和分岔图如图2所示。当a=0.7，1.2，1.4，1.8，4.0，4.2，4.8时，系统(2)分别表现为周期、单涡卷、双涡卷、四涡卷、拟周期、周期、四涡卷状态。其x-y平面相图如图3所示。由图2和图3可知，当a∈[0，5]时，随着a的增加，系统(2)运动状态开始从周期到单涡卷吸引子，再从单涡卷吸引子到双涡卷吸引子，然后经过四涡卷吸引子和拟周期状态，最后从周期变为四涡卷吸引子。当a∈(5.0，5.4]∪(5.8，6.6]∪(10.2，11.5]∪(23.0，35.0]时，系统(2)最大Lyapunov指数近似为0，此时系统(2)表现为周期运动形式；当a∈(5.4，5.8]∪(6.6，10.2]∪(11.5，23.0]时，系统(2)处于混沌状态。其中a=5.2，25.0时的相图如图3所示。

(a)Lyapunov指数谱

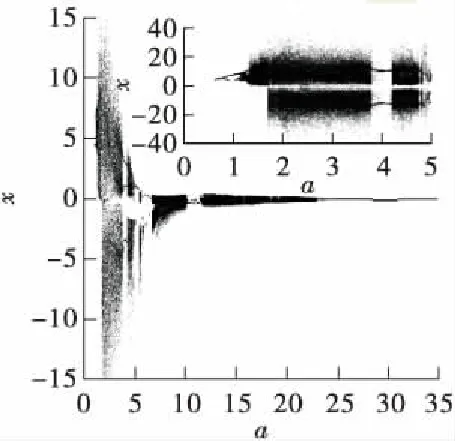
(b)分岔图

Fig.2 Lyapunov exponent spectra and bifurcation diagram of the system(2)with varied parametera

(a)a=0.5

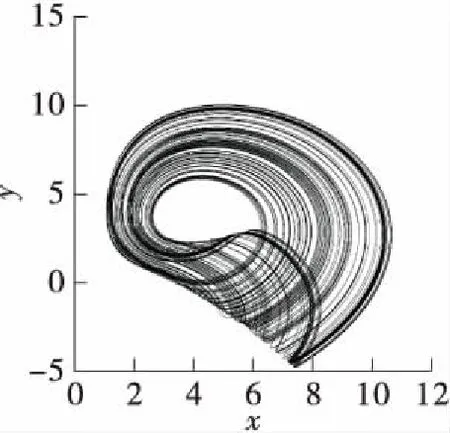
(b)a=1.2

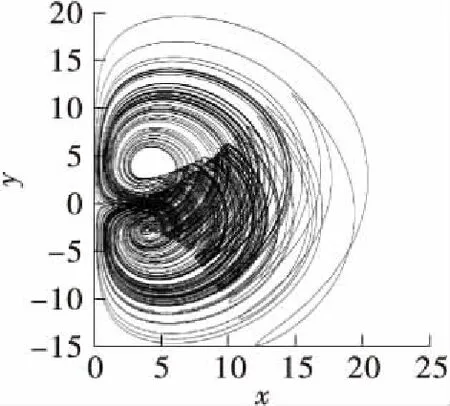
(c)a=1.4

(d)a=1.8

(e)a=4.0

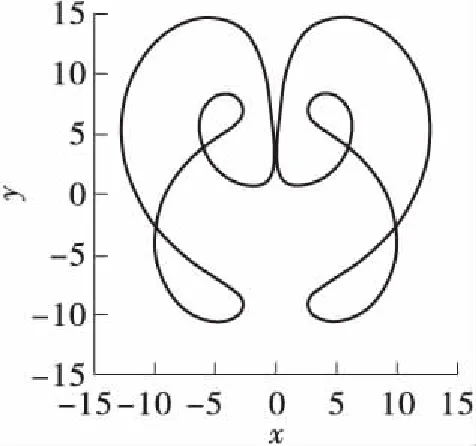
(f)a=4.2

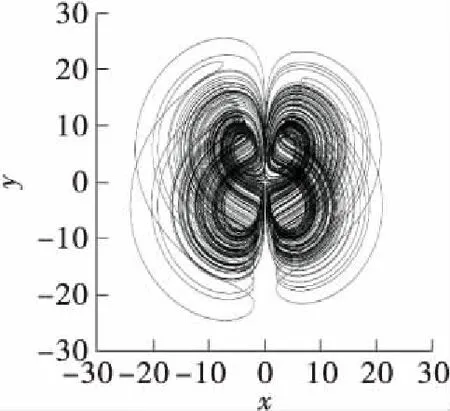
(g)a=4.8

(h)a=5.2

(i)a=25.0

2.2 参数b 对系统特性的影响

取系统参数a=1.0，c=4.8，初始值为[1，2，3，4]。当b∈[-5.00，3.00]时，系统(2)的Lya-punov指数谱和分岔图见图4。从图4可知，系统(2)整体运行状态随系统参数的变化频繁地在周期和混沌状态之间切换，当b∈[-5.00，-3.90]∪(-3.75，-3.00]∪(-0.64，-0.60]∪(-0.56，-0.52]∪(1.24，1.52]，系统(2)最大Lyapunov指数近似为0，此时表现为周期运动形式。当b∈(-3.90，-3.75]∪(-3.00，-0.64]∪(-0.60，-0.56]∪(-0.52，1.24]∪(1.52，3.00]，系统(2)处于混沌状态。

(a)Lyapunov指数谱

(b)分岔图

Fig.4 Lyapunov exponent spectra and bifurcation diagram of the system(2)with varied parameterb

2.3 参数c对系统特性的影响

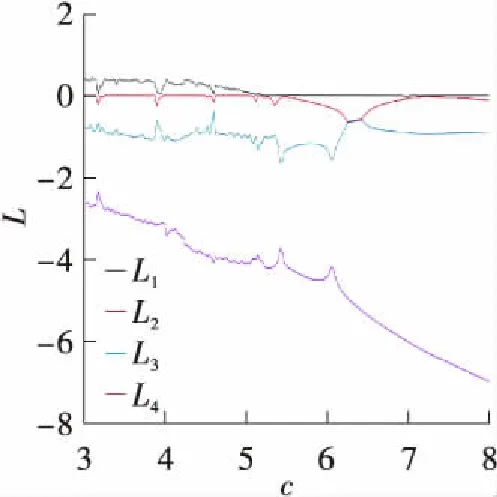
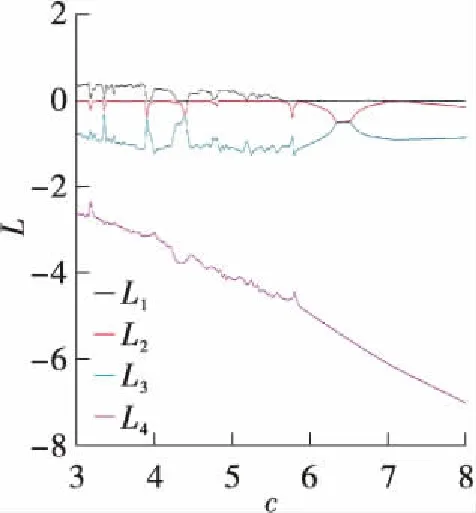
取系统参数a=1.0，b=1.6，初始值为[1，2，3，4]。当c∈[3.00，8.00]时，系统(2)的Lyapunov指数谱和分岔图如图5所示。从图5可知，系统(2)整体运行状态随系统参数的变化频繁地在周期和混沌状态之间切换，其中当c∈[3.000，3.250]∪(3.800，3.875]∪(4.125，4.250]∪(4.850，4.900]∪(5.175，8.000]，系统(2)最大Lyapunov指数近似为0，此时系统(2)表现为周期运动形式；当c∈(3.250，3.800]∪(3.875，4.125]∪(4.250，4.850]∪(4.900，5.175]，系统(2)处于混沌状态，并且系统(2)在c=5.238、c=5.425、c=6.860和c=7.188处出现倍周期分岔。

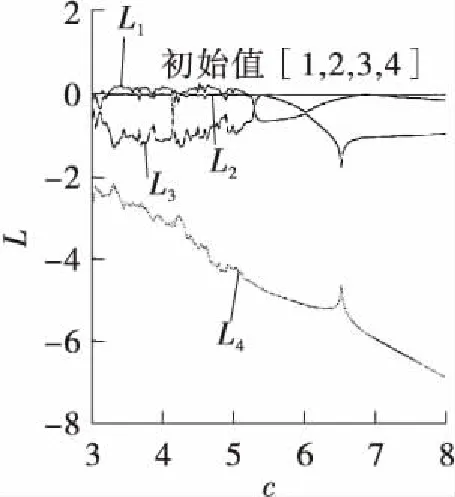
(a)Lyapunov指数谱

(b)分岔图

Fig.5 Lyapunov exponent spectra and bifurcation diagram of the system(2)with varied parameterc

3 多种吸引子共存类型

在一定的参数组合下，不同的初值组合导致系统的运行轨迹不同，一些运行轨迹最后都收敛在同一个吸引子上，而有些运行轨迹则收敛在其他的吸引子上，称这些吸引子为共存吸引子[42]。如果他们具有不同的吸引子，相同的动力学行为，则称为齐次共存吸引子。如果它们具有不同的动力学行为，不同的吸引子，则称为异质共存吸引子[17，43]。

3.1 参数a变化下的共存

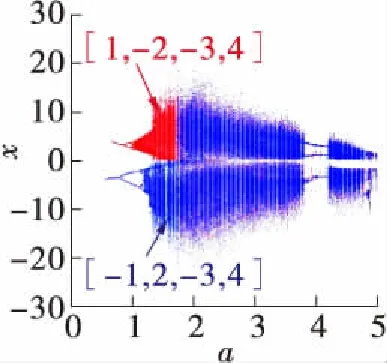
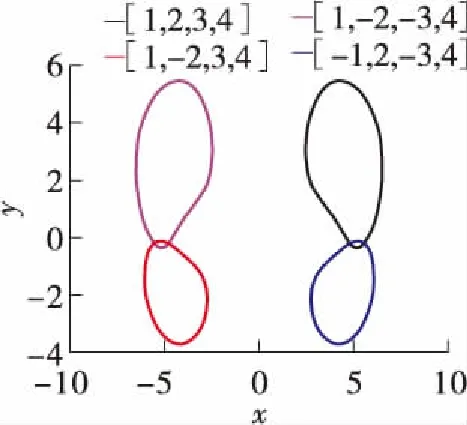
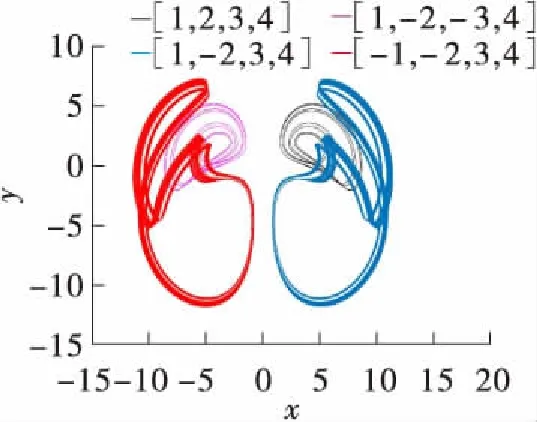
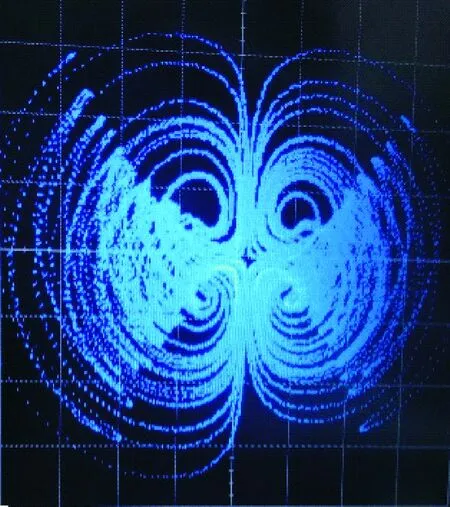
系统参数b=1.0，c=5.6，当0

当a=0.2，0.7，1.4时，系统分别表现为4个点吸引子共存、4个周期1吸引子共存、2个双涡卷吸引子共存。其共存的x-y平面相图如图7所示。

(a)b=1.0，c=5.6

(b)b=1.0，c=5.6

(c)初始值为[1，-2，3，4]

(d)初始值为[1，-2，-3，4]

(e)初始值为[-1，2，-3，4]

表1 参数a变化下的系统(2)共存类型

Table 1 Coexistence types of system(2)with varied parametera

a的取值范围初始值共存类型(0.600,0.975][1,2,3,4],[1,-2,3,4]周期吸引子共存(0.975,1.150][1,2,3,4],[1,-2,3,4]周期与混沌吸引子共存(1.150,1.700][1,2,3,4],[1,-2,3,4]混沌吸引子共存(0.575,1.000][1,-2,-3,4],[-1,2,-3,4]周期吸引子共存(1.000,1.150][1,-2,-3,4],[-1,2,-3,4]周期与混沌吸引子共存(1.150,1.650][1,-2,-3,4],[-1,2,-3,4]混沌吸引子共存

3.2 参数b变化下的共存

系统参数a=1.0，c=4.8，当-5.0

(a)a=0.2

(b)a=0.7

(c)a=1.4

Fig.7 Phase diagrams inx-yplane with different initial values and varied parametera

(a)a=1.0，c=4.8

(b)a=1.0，c=4.8

(c)初始值为[1，-2，3，4]

(d)初始值为[1，-2，-3，4]

(e) 初始值为[-1，2，-3，4]

当b=-5.0，-3.8，-2.5，1.6时，系统(2)分别表现为2个周期1吸引子共存、混沌与拟周期共存、2个混沌吸引子共存、4个混沌吸引子共存，其共存的x-y平面相图分别如图9(a)-(d)所示。当a=1.0，b=-3.0，c=4.8时，初始值分别取[1，2，3，4]、[1，-2，3，4]、[1，2，-3，4]和[-1，-2，3，4]时，2个混沌吸引子与2个周期4吸引子共存，其共存的x-y平面如图9(e)所示。当a=1.0，b=0.5，c=4.8，初始值分别取[1，-2，3，4]、[1，-2，-3，4]、[-1，2，-3，4]、[1，2，3，-4]以及[1，-2，-3，4]时， 3个混沌吸引子和2个周期1吸引子共存，其共存的x-y平面如图9(f)所示。

表2 参数b变化下的系统(2)共存类型

Table 2 Coexistence types of system(2)with varied parameterb

b的取值范围初始值共存类型(-5.000,-4.264),(-3.688,-3.016],(-0.872,-0.616][1,2,3,4],[1,-2,3,4]周期吸引子共存(-3.900,-3.750),(-1.000,-0.872][1,2,3,4],[1,-2,3,4]混沌与拟周期吸引子共存(-3.016,-1.000],(-0.552,1.240],(1.520,3.000][1,2,3,4],[1,-2,3,4]混沌吸引子共存(-0.600,-0.552],(1.240,1.520][1,2,3,4],[1,-2,3,4]周期与混沌吸引子共存(-5.000,-4.008],(-3.560,-3.016][1,-2,-3,4],[-1,2,-3,4]周期吸引子共存(-4.008,-3.560][1,-2,-3,4],[-1,2,-3,4]周期与拟周期吸引子共存(-3.016,-1.544],(-1.000,-0.296],(-0.200,2.800][1,-2,-3,4],[-1,2,-3,4]混沌吸引子共存(-1.544,-1.320][1,-2,-3,4],[-1,2,-3,4]混沌与拟周期吸引子共存(-1.320,-1.000],(-0.296,-0.200][1,-2,-3,4],[-1,2,-3,4]周期与混沌吸引子共存

(a)a=1.0，b=-5.0，c=4.8

(b)a=1.0，b=-3.8，c=4.8

(d) a=1.0，b=1.6，c=4.8

(e) a=1.0，b=-3.0，c=4.8

(f)a=1.0，b=0.5，c=4.8

Fig.9 Phase diagrams inx-yplane with different initial values and varied parameterb

3.3 参数c变化下的共存

系统参数a=1.0，b=0.6，当3.0

(a)a=1.0，b=0.6

(b)a=1.0，b=0.6

(c)初始值为[1，2，3，4]

(d)初始值为[-1，2，-3，4]

(e)初始值为[1，-2，-3，4]

(f)初始值为[1，-2，3，4]

图10 参数c变化时系统(2)的共存分岔图和Lyapunov指数谱

Fig.10 Coexistence bifurcation diagram and Lyapunov exponent spectra of system(2)with varied parameterc

图11 参数a=1.0，b=0.6，c=5.6的x-y平面相图

Fig.11 Phase diagrams inx-yplane whena=1.0，b=0.6，c=5.6

表4总结了系统(2)共存吸引子的对应参数值、初始值、最大李雅普诺夫指数(MLEs)，其中Lk、Lb、Lr、Lp、Lg分别表示黑色、蓝色、红色、粉红色、灰色吸引子的MLEs。

表3 参数c变化下的系统(2)共存类型

Table 3 Coexistence types of system(2)with varied parameterc

c的取值范围初始值共存类型(3.000,3.875],(3.950,5.075],(5.125,5.175][1,2,3,4],[-1,2,-3,4]混沌吸引子共存(3.875,3.950][1,2,3,4],[-1,2,-3,4]拟周期吸引子共存(5.075,5.125],(5.175,8.000][1,2,3,4],[-1,2,-3,4]周期吸引子共存(3.000,3.875],(3.950,4.225],(4.425,5.625][1,-2,-3,4],[1,-2,3,4]混沌吸引子共存(3.875,3.950][1,-2,-3,4],[1,-2,3,4]拟周期吸引子共存(4.225,4.425],(5.625,8.000][1,-2,-3,4],[1,-2,3,4]周期吸引子共存

表4 不同参数和初始值下的共存吸引子

通过上述分析可知，系统(2)在不同的参数和初始值下出现了多种吸引子共存类型，多个吸引子的共存意味着系统对参数和初始值的敏感性。参数和初始值的变化亦导致系统的动态演化与倍分岔的发生。

4电路仿真

4.1 基于Multism的模拟电路设计与仿真

利用Multisim电路仿真软件，采用线性电阻、电容、LM2924N运算放大器、AD633模拟乘法器，实现了该混沌系统的电路设计与仿真。根据混沌系统动力学方程，设计的电路原理图如图12所示，其中乘法器的输出增益为0.1。根据系统(2)的电路原理图，系统自激振荡方程为：

(7)

图12 电路原理图

其中，R1-R24为电阻，C1-C4为电容，t为时间。取电容C1=C2=C3=C4=1μF，R6=R7=R17=R18=R23=R24=100 kΩ，R5=R11=R16=R22=1 kΩ。

(8)

当a=1.4，b=1.0，c=5.6，通过对比方程(7)和(8)，并保持相应的系数相等，可得电阻值为：

取初始值为[1，2，3，4]，图13(a)为示波器上观察到的结果。当a=1.8，b=1.0，c=5.6以及a=1.0，b=1.6，c=4.8时，示波器上显示的结果分别为图13(b)-13(f)。可以看出实验结果与数值仿真结果完全相符。

(a)a=1.4，b=1.0，c=5.6

(b)a=1.8，b=1.0，c=5.6

(c)a=1.0，b=1.6，c=4.8

(d)a=1.0，b=1.6，c=4.8

(e) a=1.0，b=1.6，c=4.8

(f)a=1.0，b=1.6，c=4.8

4.2 基于现场可编程门阵列的数字电路设计与仿真

采用欧拉算法对系统(2)进行离散化处理，得到如式(9)所示差分方程，其中参数a=1.4，b=1.0，c=5.6，迭代步长Δt=0.001。

(9)

式中，n=0，1，2，…。

编译后的Xilinx RTL原理图如图14所示。当初始值为[1，2，3，4]时，通过示波器观察到的波形如图15(a)所示。当a=1.8，b=1.0，c=5.6以及a=1.0，b=1.6，c=4.8时，示波器上显示的结果分别为图15(b)-15(f)所示，可以看出，FPGA数字电路实现结果与Multisim模拟电路仿真结果以及Matlab的数值仿真结果相符。