基于马尔科夫奖励过程的牵引系统可靠性评估
2020-04-29李小波陆朱剑程岳梅田世贺
李小波, 褚 敏, 陆朱剑, 程岳梅, 田世贺
(上海工程技术大学 城市轨道交通学院, 上海 201620)
0 引 言
地铁列车牵引系统是保证地铁安全可靠运行的关键系统,对牵引系统的可靠性评估有利于提高地铁的安全性能,改进安全维修周期,节约人力物力成本。赵峰等人[1]通过对动车组列车牵引传动系统分层分析,以组合赋权法计算指标层组合权重,最终采用模糊灰色聚类法完成了对系统的健康状态评估;曹茜等人[2]根据CRH3型动车组的运行历史数据,结合蒙特卡罗模拟-元胞自动机(MCS-CA)算法,分析计算了牵引传动系统不同状态下的可用度变化;孟辉苓等人[3]分析对比系统关键器件不同的故障机理从而得到牵引逆变系统的可靠性逻辑表达式,建立了城轨列车牵引逆变系统的可靠性评估模型;宋永丰等人[4]通过分析牵引传动系统各部件对系统的影响程度及可靠性逻辑关系,建立了牵引传动系统的可靠性模型,并采用专家评分分配法对各部分完成了可靠性分配,对地铁列车牵引系统的可靠性评估有参考意义;赵琼[5]采用故障树分析法对牵引供电系统接触网开展了定性和定量分析,并结合马尔科夫模型考虑维修因素对接触网系统进行可靠性分配;郑彦涛[6]从系统检修的角度,考虑系统设备的重要度对动车组系统功能进行层次分析,建立了列车系统维修可靠性模型。
既有文献在进行牵引系统可靠性评估时未全面考虑各子系统对整个系统的影响程度,不同子系统权重不同,对于整个系统的状态评估影响不同。因此,本文通过对牵引系统进行层次分析确定系统的可靠性评估指标,并计算不同子系统对于牵引系统的组合权重,进而确定进入故障状态的奖励系数,采用马尔科夫奖励过程分析牵引系统考虑不同衰减系数,建立了地铁列车牵引系统可靠性评估模型。
1 基本理论
1.1 系统可靠性
可靠性是指在规定条件下和规定时间内完成规定功能的能力,是系统综合性能的体现。维修可靠性参量主要有可靠度、故障率、修复率、可靠寿命、失效前平均工作时间等,本文在建立牵引系统可靠性评估模型时主要用到故障率以及修复率两个可靠性参量。
故障率是指工作到某时刻t时尚未发生故障的产品,在t时刻以后的下一个单位时间内发生故障的概率,也称失效率。记为λ(t);λ(t)的数学定义可表示为:
(1)
其中,Δn(t)指到t时刻为止处于故障状态的产品数,R(t)指起始时刻处于工作状态的产品数。
修复率是指维修时间已达到某一时刻t但尚未修复的产品,在t时刻后的下一个单位时间内完成修复的概率[7], 记为μ(t)。μ(t)的数学定义可表示为:
(2)
其中,ΔM(t)表示到t时刻为止被修复的产品数,G(t)指从起始时刻处于故障状态及到t时刻为止新发生故障的产品数之和。
1.2 层次分析法
层次分析法的基本思想是将复杂系统划分成多个子系统、归结为多个影响因素,并将相同子系统的每一个影响因素相互对比、判断和计算以得到不同子系统对于整个系统的权重,给系统状态分析提供参考。具体实施步骤如下:
步骤1将目标系统分层分析构建出系统结构模型,并将其影响因素作为指标层,自底而上分析系统性能。
步骤2判断指标层每个因素之间的相对重要性,比例标度法取值及定义见表1,由此构造出判断矩阵R。

表1 比例标度法取值及定义
步骤3采用公式CR=CI/RI对判断矩阵R进行随机一致性检验。其中,CR为判断矩阵R的一致性比率,CI为一致性指标,CI=(λmax-n)/(n-1),RI表示其平均一致性指标,多阶成对比较矩阵RI的取值见表2。由表2判断RI的取值。
表2 多阶成对比较矩阵RI的取值
Tab. 2 The value of the multi-order pairwise comparison matrixRI

N12345678RI000.580.91.121.241.321.41
步骤4自适应满足步骤3一致性检验后,由公式RZ=λmaxZ求解组合权重,其中λmax表示R的最大特征根,Z为λmax的对应特征向量。
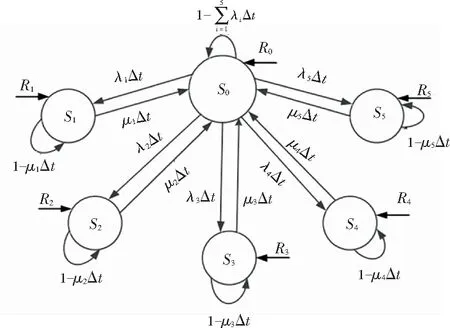
当n≥3且0 (3) 其中, (4) 设{X(t),t≥0}表示在评估系统时取值在有限个系统状态集S={0,1,…}上的一个随机过程,其中X(t)表示系统在t时刻所表现出的状态。若对于在任意自然数n以及任意时刻点0≤t1 P[X(tk+1=j)|X(tk+1=i)]=Pij, (5) 考虑到进入不同系统状态的影响,在马尔科夫过程的基础上增加状态奖励Ms和衰减系数γ。Gt表示整个马尔科夫奖励过程从时刻t开始所有奖励并带有衰减的总和。研究推得其数学公式为: (6) Ms=E{Mt+1|St=S}表示在{X(t),t≥0}状态下某时刻t处进入下一个时刻t+1能获得的期望奖励。其中,衰减系数γ∈[0,1]表示之后的奖励在当前状态的价值比例,在t+1时刻获得的奖励M在t时刻的体现出的价值γkM,价值评估函数v(s)给出了某一状态的价值,其公式即如式(7)所示: v(s)=E[Gt|St=s]= E[Mt+1+γMt+2+γ2Mt+3+…|St=s]= E[Mt+1+γ(Mt+2+γMt+3+…)|St=s]= E[Mt+1+γGt+1|St=s]= E[Mt+1+γv(St+1)|St=s], (7) 用s′表示s状态下一时刻的任何可能的状态,则价值评估方程表达为: (8) 研究可知,v=M+γPv经变换后得到: v=(1-γP)-1M. (9) 在对系统进行价值评估时,必须确定不同状态的奖励系数以及衰减系数。在确定奖励系数时容易受到主观判断的影响,不合理的奖励系数会使得评估系统价值的结果产生很大误差,故将1.2节中所求综合权重a作为奖励系数。若衰减系数γ接近0,表明本次为近似性评估,γ愈靠近1,则表明偏重考虑远期的利益。因此分别选取0.2,0.5,0.9作为衰减系数从不同角度考虑评估系统价值。 地铁列车牵引系统可分为受电弓模块、断路器模块、牵引逆变模块、牵引电机模块以及控制模块等5个模块。其中,受电弓模块故障形式主要有升降弓机械故障以及电机损坏、绝缘子失效、碳滑板磨损到限等;断路器模块故障形式主要有辅助触点故障、控制线圈烧损故障、机械结构故障等;牵引逆变模块故障形式主要是二极管击穿导致IGBT损坏;牵引电机模块故障形式主要有电机速度传感器故障、电机损坏不能运行等;控制模块故障形式主要有软件缺陷、电气零部件老化或质量问题造成的故障;在处理故障数据时以上述故障形式为基准计算各模块的故障率以及修复率。 利用层次分析法对地铁列车牵引系统进行分析时,考虑到各模块的元件十分复杂并大都相互关联,如果采用元器件级的评价指标进行系统可靠性评估,会使得整个系统的可靠性评估过程冗长且不准确。故从各个模块的工作环境、重要程度、复杂程度以及技术成熟程度等方面综合评估系统的可靠性,共分为系统层、模块层以及指标层三层。地铁列车牵引系统分层建模分析结构图如图1所示。由图1可知,系统层用于表达系统状态,模块层为系统各模块的状态评估,指标层考虑不同模块的组成特性、运行环境等确定评价指标。自底向上逐层分析,确定各模块对于牵引系统的权重值,即奖励系数M。 图1 地铁列车牵引系统分层分析结构图 Fig. 1 Hierarchical analysis structure diagram of subway train traction system 根据系统状态转移图求解状态转移概率方程组: (10) 图2 牵引系统马尔科夫状态转移模型 为了求得稳态概率,令Δt→0,得到线性方程组矩阵为: 且∑Pi=1, (11) 求得: (12) 结合公式(9)得到牵引系统的稳态可靠度,即: (13) 牵引系统是一个极其复杂的系统,在分析系统可靠性时,考虑系统各模块的复杂程度、重要程度、技术成熟程度、工作环境来自底向上分析整个系统的可靠性。根据文献[4]得到表3,以表3的数据为参考构建判断矩阵来进行层次分析。 表3 可靠性评估指标 构建判断矩阵时,对受电弓模块而言,可得: 求解R的最大特征值λmax=4.027 7,CI=0.009 2。 检验计算得CR=0.001满足要求,所以相应的权重值就是对应的特征向量。研究得到: z1=[0.435 2,0.123 3,0.435 2,0.778 5], 同理求得: z2=[0.166 1,0.278 7,0.482 6,0.813 5], z3=[0.813 5,0.278 7,0.482 6,0.166 1], z4=[0.250 5,0.467 4,0.250 5,0.809 9], z5=[0.827 3,0.146,0.522 4,0.146] 根据式(3)计算得到: a1=0.5,a2=0.5,a3=-0.6,a4=0.5,a5=0.5, 即: z0=[0.5,0.5,-0.6,0.5,0.5], 最终计算可得a0=0.2,即M0=0.2。 以某地铁线路AC车型2015年列车故障数据作为参考,考虑不同时期的系统可靠性变换,分别设γ=0.2/0.5/0.9对应从短期、中期、长期的角度评估牵引系统可靠性变化趋势。牵引系统可靠度评估对比结果如图3所示。 图3 牵引系统可靠度对比图 不难看出,不同考虑角度的系统可靠度下降趋势一致,考虑长期系统状态可靠度下降较前两种缓和一些,3种时期系统可靠度都在30天后下降趋于平缓。对比3种曲线,为确保行车安全,应选择考虑短期利益的近似性评估作为检修计划的参考标准,当系统可用度降低到0.9时作为检修阈值,对应图3得到:当可用度降低到0.9时为3.5天,故针对该线路牵引系统的故障数据,应设立检修周期为3天作为牵引系统检修计划制定的参考。 本文通过对系统进行层次分析确定系统的可靠性评估指标,并利用层次分析法计算组合权重确定奖励系数,采用马尔科夫奖励过程考虑不同衰减系数建立地铁列车牵引系统可靠性评估模型,最终研究确定衰减系数γ=0.2,奖励系数M=0.2作为可靠性评估最优参数,该分析方法对地铁列车的维护保障、维修决策具有重要的参考意义。1.3 马尔科夫奖励过程
2 牵引系统可靠性评估模型
2.1 可靠性指标计算
2.2 牵引系统的可靠性层次分析

2.3 马尔科夫奖励过程可靠性评估

3 实例分析
3.1 可靠性评估参数的确定


3.2 可靠性评估

4 结束语
