基于NVIDIA JetSon TX2的无人机双目测距算法设计
2020-04-29樊建昌尚钲历
樊建昌, 余 粟, 尚钲历
(1 上海工程技术大学 机械与汽车工程学院, 上海 201620; 2 上海工程技术大学 工程实训中心, 上海 201620; 3 上海星河湾双语学校, 上海 201108)
0 引 言
随着无人机技术和计算机科学技术的不断发展,无人机在商业上的应用场景越来越广泛,从最初的视频业务如AR/VR、无人机航拍、物流无人机到后来的智能落地物联网、基础设施巡检、无人安防等领域再到如今AI时代正大力发展的互联网产品,所有的信息都表明了无人机巨大的商用价值。但是随着无人机应用领域的逐渐扩大,各个应用场景对无人机的性能要求越来越高,主要包括无人机的续航能力、拍摄、避障等关键技术。其中无人机的避障技术由于直接关乎到无人机的安全性,因此一直以来都是科研人员在无人机研究领域的重点和热点问题。潘枭等人[1]提出了一种基于毫米波雷达的多旋翼无人机避障技术的设计方案。此方案通过机载避障传感器毫米波雷达来实现多旋翼无人机避障功能;刘跃波等人[2]针对无人机电力巡检的应用场景,提出了基于T - S 模糊神经网络,建立模糊控制规则来对无人机的实时避障进行仿真;金立军等人[3]结合定位技术和激光测距技术,先通过惯性测量系统进行初步定位,得到无人机的经纬度坐标,然后利用无人机机载激光测距模块,测量故障点到无人机的距离来达到无人机避障的目的;饶俊[4]利用了单载波频域均衡(SCFDE)技术以及优化遥控帧与伪码速率关系及发送位置的方法,降低了机上测距数据下传误码率,提高了无人机系统的测距精度。与前述研究不同的是,本文利用被动测距技术中的双目视觉测距技术,以NVIDIA Jetson TX2智能AI计算模块为计算平台,以SGBM立体匹配算法为基础,设计了无人机测距系统,在图像分辨率为376*240、平均误差为4.87%的情况下,测距长度上达到了7 m,帧率达到了8.9帧,基本上满足了无人机飞行过程中的实时性要求。
1 摄像机成像模型
常见的理想状态下摄像机成像模型如图1[5]所示。模型中包含了4个坐标系,分别是:世界坐标系、相机坐标系、图像坐标系以及图像像素坐标系。其中,物体上的任意一点P在世界坐标系中的位置记为(Xw,Yw,Zw),在摄像机坐标系xoy中的坐标为(X,Y,Z),在图像像素坐标系XfOYf中的坐标为(u,v),结合三角形相似推得点P由世界坐标系到图像像素坐标系的转化过程可由式(1)表示[6]:
M*N*Pw.
(1)
其中,s为缩放因子;M为摄像机的内参数矩阵,描述了点P由相机坐标系到图像坐标系的转化关系,M由相机自身的安装精度及透镜特性决定;N为点P由世界坐标系到相机坐标系的转换矩阵,称为摄像机模型的外参数矩阵;R3*3=[r1,r2,r3]是一个正交矩阵,T3*1=t3*1。二者分别为点P由世界坐标系转换到相机坐标系的旋转矩阵和平移矩阵。内参数矩阵M以及外参数矩阵N可以由单目相机标定求得。

图1 摄像机成像模型
2 双目测距的基本原理
双目立体视觉测距主要是利用双目相机从不同视角拍摄同一物体时在图像中得到的不同位置信息来计算图像的视差信息,进一步利用三角形相似的原理求解出物体的三维坐标信息来达到求解物体的距离。其原理图如图2所示。
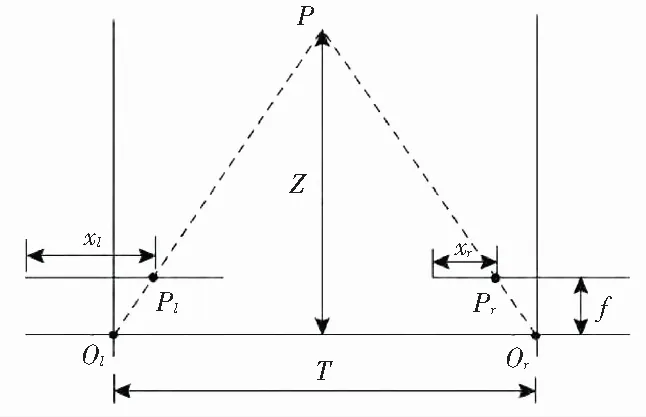
图2 双目成像原理
在图2的平行双目成像系统中,P表示待测目标上的某一点,Ol、Or分别表示左右摄像机坐标系的原点(左右相机的光心),Pl、Pr分别表示P在左右相机CCD芯片上的投影点,由图2的摄像机成像模型易得,Ol、Or与左右相机的CCD芯片的中心连线垂直于Pl、Pr所形成双目基准平面。xl、xr分别为物体上的P在左右相机成像平面的投影点到成像平面左边界的物理距离,f为相机焦距,T为双目相机左右光心之间的物理距离,Z为物体距离摄像机水平面的真实的物理距离[7]。
观察图2,由ΔPPlPr~ΔPOlOr得:
(2)
将PlPr=T-(Xl-Xr) 代入式(2)得:
(3)
由相机坐标系和图像坐标系的转换关系可得:
xr-xl=(ul-ur)*dx,
(4)
其中,dx表示在图像坐标系中,每个像素在CCD芯片上所占的实际物理尺寸的大小。将式(4)代入式(3)得:
(5)
(6)

2.1 双目标定原理
双目标定是双目系统中求取左右相机之间的旋转矩阵R以及平移矩阵T的过程。 由图1~图2可得,在不考虑摄像头畸变和相机水平摆放的误差的前提下,物体点P由世界坐标系投影到相机坐标系可以用式(7)来表示:
(7)
进一步可得右相机到左相机的旋转矩阵及平移矩阵如下[8]:
(8)
其中,R、T即为右相机到左相机的旋转矩阵和平移矩阵。
2.2 立体校正
在实际的双目测距项目中,双目相机由于安装工艺的缺陷常常导致实际的安装情况如图3所示[9],这会使得后期的立体匹配需要在二维方向上进行。所以,在实际的测距过程中,在立体匹配之前常常使用Bouguet立体校正使双目相机的左右成像平面平行,并且使得物体在左右图像上的投影点位于同一水平线上。这样做的目的是通过运用极限约束原理使得同一物体在左右两幅图像中的搜索范围从二维降到了一维。
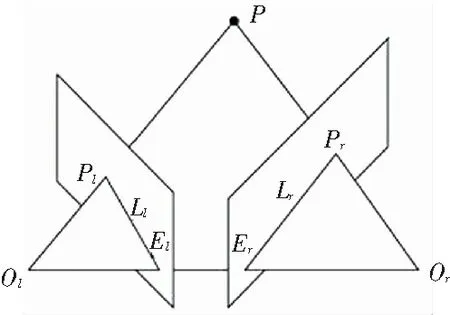
图3 双目成像系统
Bouguet校正矩阵的求解主要分为2步,对此可得阐释分述如下。
(1)求解左右相机共面校正矩阵。由于R是正交实矩阵,则R是正规矩阵[10],所以有:
R=S*D*S-1,
(9)
其中,D为主对角元素为R的特征值组成的矩阵,S为R的特征向量组成的矩阵。进一步拆分式(9)可得:
(10)
令:
(11)
则将2个相机之间的旋转矩阵R划分为左右相机的合成矩阵Rl、Rr,可以实现左右图像平面共面。但是行没有对齐。
(2)求解行对校正矩阵。 根据式(12)建立行对准矩阵Rrect。其中,T为由右相机到左相机的平移矩阵。
综合以上2步分别计算左右相机的行对准变换矩阵,即:
(12)
(13)
2.3 立体匹配
立体匹配是双目测距中最关键的一部分,本文选用立体匹配中最常用的SGBM算法作为双目测距中的立体匹配算法,其原理为[11]:确定左右图像的匹配基元;构建基于多个方向扫描线的代价能量和函数;求取能量代价和函数的最优解。该算法在OpenCV中的实现流程具体如下。
(1)预处理。SGBM采用水平Sobel算子,把图像做处理,再用一个函数将经过水平Sobel算子处理后的图像上每个像素点(P表示其像素值)映射成一个新的图像,Pnew表示新图像上的像素值。映射函数如下:
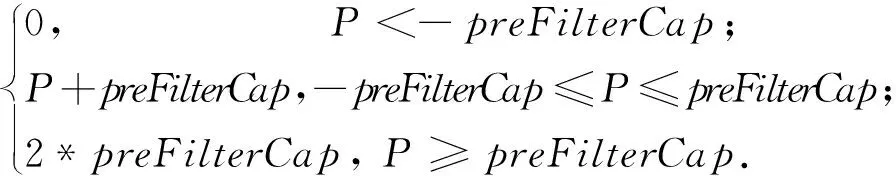
(14)
其中,preFilterCap是一个常数参数,OpenCV缺省情况下取15。
(2)代价计算。由2部分组成:
① 经过预处理后得到的图像的梯度信息利用基于采样[12]的方法得到的梯度代价。
② 原图像经过基于采样的方法得到的SAD代价,其计算公式如下:
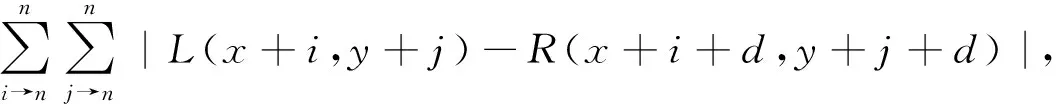
(15)
(3)动态规划。SGBM算法试图通过图像上多个方向上一维路径的约束,来建立一个全局的马尔科夫能量方程,每个像素最终的匹配代价是所有路径信息的叠加,每个像素的视差选择都只是简单通过 WTA(Winner Takes All)决定的。多方向能量聚集如图4所示。其中,每个方向都按照动态规划的思想进行能量累积,再将所有方向的匹配代价相加得到总的匹配代价,其计算公式可表示为:

图4 能量聚集方向
Lr(p,d)=c(p,d)+
其中,L为当前路径累积的代价函数;P1、P2为像素点与相邻点视差存在较小和较大差异情况下的平滑惩罚,P1 (16) (4)后处理。主要包括如下内容:匹配窗口内的视差唯一性检测;亚像素插值;左右一致性检测;连通区域的检测。 本文以NIVIDIA JetSon TX2 为处理平台和小觅S1030(入门版)双目摄像机搭建实验平台,详见图5。这里,给出研究实验流程及结果的分析表述如下。 (1)本文以单元格大小为5 m*5 m的12*9高精度棋盘格作为标定板,左右相机分别采集29张标定板图像,经过预处理后利用张氏标定法[13]对其进行标定,得到左右相机的内参数矩阵以及各自的畸变参数,标定结果界面如图6所示,标定结果数值具体如下: Dl=[-250.357 6,505.793 9,-705.366 3, -851.954 5,0.000 0] Dr=[-303.763 8,799.294 3,515.475 4, -672.489 0,0.000 0] 其中,Ml、Mr分别为左右相机的内参数矩阵,Dl、Dr分别为左右相机的畸变参数矩阵。 图5 实验平台 图6 标定结果 (2)选取29组左右相机的图片,标定板图片的分辨率为752*480。利用OpenCV视觉库编写双目标定程序,以左相机坐标系作为双目标定的基准坐标系,通过OpenCV中的stereoCalibrate()函数计算得到旋转矩阵R和平移矩阵T结果如下: T=[-1.200 248 976 4e+02,-1.178 263 74e+00,-5.205 820 51e+00] (3)利用(1)中得到的左右相机的内参数和畸变参数,以及(2)中的得到的左右相机之间的外参数,再利用通过OpenCV视觉库中的cvStereoRectify()和initUndistortRectifyMap()函数计算出左右相机的立体校正和畸变校正参数矩阵。 (4)利用OpenCV视觉库中的remap()函数对左右图像进行立体校正和畸变校正,使得左右相机图像处于行对准的理想状态。 (5)以SGBM立体匹配算法为基础,利用OpenCV视觉库编写双目测距的运行算法,计算出左右图像的视差图。在此基础上,进一步利用OpenCV视觉库中的cvReprojectImageTo3D()函数计算得到障碍物距离双目相机的距离,其中SGBM算法中的相关参数设置及含义如图7所示。 图7 SGBM算法及参数 本文在以NVIDIA JetSon TX2为计算平台上,选取3 m、5 m、7 m作为双目测距的基准距离,在近似于无人机空中飞行的简单场景下,采用20次测量结果取平均值,得到的实验结果见表1。 表1 双目测距实验结果 由实验结果可得,对于SGBM算法,在752*480的分辨率下,本文设计的双目系统测距的准确度要高于376*240的准确率,但是在实时性上,752*480的分辨率在4.6帧左右,很难满足无人机的高速飞行,在376*240的分辨率下,当测量距离在7 m时,测距误差在4.8%左右,其测距的准确性上不如752*480的分辨率,但是其帧率达到了8.9帧,基本满足了无人机在高速飞行时的实时性要求。 与此同时,本系统也仍存在一定的问题,例如在单目标定时,由于所用的标定板过小,导致标定得到的相机的内参数和外参数的精度还有待提高。测距的准确度也亟需改善,实时性上还可以基于CUDA加速做进一步的加速计算,本系统仍有很大的提升空间。3 实验流程及结果




4 结束语
