面向健康医疗的分类关联规则挖掘研究
2020-04-29孙明瑞臧天仪
孙明瑞, 臧天仪
(哈尔滨工业大学 计算机科学与技术学院, 哈尔滨 150001)
0 引 言
数据挖掘技术是从海量数据集中挖掘出用户感兴趣的物品或知识,这些知识是隐式的、未知的,挖掘出的知识表示为定律、规律、规则等形式。关联分析(Association Analysis)是数据挖掘的基础,用以挖掘大规模、海量数据中隐式的规则关系模式。大规模数据间存在关联关系,变量的取值也存在某种规律性,但数据间的关系是复杂的、隐式存在的,关联分析的目的就是挖掘数据间的隐藏关联信息,对健康医疗领域具有新的价值。典型的规则如购物篮事务(Market Basket Transaction),“如果用户购买了婴儿尿布,那么该用户购买啤酒的概率为33%”,产生的关系可以用关联规则(Association Rule)或频繁模式(Frequent Pattern)表示,用以反映用户偏好的有用规则。
基于以上的分析和讨论,本文提出了针对个人健康信息数据的频繁特征项挖掘算法,扩展了关联规则频繁模式的概念,引入连续性特征属性值并给出离散化的解决方案,改进了关联规则的一般模式,提出了分类关联规则挖掘算法,对健康医疗领域和其它领域中基于关联规则的推荐具有重要的指导意义和研究价值。
1 相关工作
关联规则挖掘是数据挖掘的一个重要研究方向,描述了交易数据集中2组不同对象之间存在的某种关联关系。在关联规则挖掘过程中,需要对交易数据集进行多次扫描并与候选频繁项目集进行匹配和计数。由于面对巨量交易数据集,这一匹配和计算过程需要花费大量时间,因此效率是设计算法的关键。
1994年Agrawal等人[1]开创性地提出了Apriori算法,用来发现购物篮中有趣的关联关系,基于“所有长频繁项目集的子集都是频繁”的思想,对候选频繁项目集进行剪枝,使候选频繁项目集更小,从而显著改进频繁项目集算法的性能。自此,学界进行了广泛的研究,来解决关联分析中的实现和应用等问题。FP-growth[2]算法实现了FP-tree的构造及在FP-tree上进行挖掘,在效率上较之Apriori算法有很大的提高。Park等人[3]在1995年提出一种高效地产生频繁项目集的基于杂凑的DHP算法。Savasere等人[4]设计了基于划分的算法。Toivonen[5]提出了一种基于采样的算法,其核心是随机从数据集中采集样本S,然后搜索S中的频繁项集。惠晓滨等人[6]提出了基于频繁模式栈变换的高效关联规则算法。以上这些算法都是从算法实现问题的角度来解决频繁项集挖掘。
分类关联规则(Class Association Rules)是对关联规则的扩展,用以区分或判别实例类标签的关联规则。1998年,Liu等人[7]率先提出了分类关联规则算法CBA。Wang等人[8]融合分类关联规则和决策树的优势,提出关联决策树ADT算法。Xu等人[9]首次提出利用原子型分类关联规则构建分类器的思想,创立了原子关联规则分类(CAAR)新技术。
综上所述,与传统的关联规则相比,分类关联规则具有更高的准确性及鲁棒性。作为一种新的特征匹配方法,如何处理连续属性特征,如何以较小的代价挖掘频繁项集,如何从大量关联规则中提取有效的分类关联规则,是本文研究的重点内容。
2 问题的定义
针对关联规则模式的挖掘,本次研究的目标是将数据的最后一列特征属性类别标识设置为关联规则的后件,即挖掘分类关联规则,而非全局关联规则。设I={i1,i2, …,in}为具有n个特征属性的数据集合(项集约束),y表示类别标识属性,且y∩I=∅。分类关联规则的挖掘目标是形如X→y的分类关联关系,其中X∈I。
3 算法研发与设计
3.1 先验性原理
一般地,包含k个项的数据集会产生2k-1个频繁项集,由于k的值可能非常大,导致项集搜索空间的时间复杂度是指数级规模的O(2n)。因此引入如下定理:
定理 先验(Apriori)原理如果一个项集是频繁的,则其所有的子集也一定是频繁的。
引理如果项集是非频繁的,则其所有超集也都是非频繁的。
性质 单调性原理设I是项的集合,J=2I是I的幂集。度量f是单调的(向上封闭的),当
∀X,Y∈J:(X⊆Y)→f(X)≤f(Y),
(1)
其中,X为Y的子集,则f(X)一定不会超过f(Y)。
另一方面,f是反单调的(向下封闭),当
∀X,Y∈J:(X⊆Y)→f(Y)≤f(X).
(2)
根据性质,如图1所示,通常可以采用自顶向下(从1维到n维的项集搜索)或自底向上(从n维到1维的项集搜索)的搜索策略挖掘频繁项集。

图1 频繁项集封闭性原则
3.2 频繁项集挖掘算法
Apriori算法基于支持度剪枝技术,采用分层的完备搜索算法(深度优先),依据性质向下封闭性,对关联规则进行挖掘,能有效防止项集的指数级增长。算法的功能是挖掘支持度大于等于minsup的项集。算法首先生成单个元素项集列表,通过扫描数据集计算满足最小支持度的项集,删除不满足最小支持度的项集。对单个元素的项集进行组合以生成2个元素的项集。然后,重新扫描数据集,删除不满足最小支持度的项集,重复该过程直到所有项集都被删除。频繁项集挖掘算法的设计描述见如下。
算法1 频繁项集挖掘算法
输入数据集I,最小支持度minsup,频繁项集个数kmax
输出频繁项集Fk
k←random integer from 1 tokmax
Ifk=1 thenFk←{i|i∈I∧σ(i)≥N×minsup} //发现所有的频繁1-项集
Else do
k←k+1
Ck←apriori-gen(Fk-1)//产生候选项集
For eacht∈Tdo
Ct←subset(Ck,t)
//识别属于t的所有候选
For eachc∈Ctdo
σ(c)←σ(c)+1
//支持度计数增值
End for
End for
Fk←{c|c∈Ck∧σ(c)≥N×minsup} //提取频繁k-项集
UntilFk=∅
Return ∪Fk
3.3 候选项集的挖掘和剪枝
候选项集挖掘通过合并频繁k-1项集,当且仅当前k-2项都相同。这里设X={x1,x2,…,xk-1}和Y={y1,y2,…,yk-1}是频繁k-1项集,合并X和Y,当其均满足如下公式:
xi=yi(i=1, 2,…,k-2)且xi-1≠yi-1.
(3)
3.4 算法的时间复杂度

3.5 分类关联规则挖掘算法
针对分类关联规则挖掘,关联规则的后件为类别标识,即形如X→y的分类关联规则。通过3.2节频繁项集挖掘,研究得到了最大频繁项集Fk,由其产生的子集可作为分类关联规则的前件,而目标类标识作为关联规则后件,是一种存在具体搜索目标的挖掘优化问题,同时需要满足设定的最小支持度和最小置信度阈值要求。这里,给出了分类关联规则挖掘算法的研发代码详见如下。
算法2 分类关联规则挖掘算法
输入频繁k项集Fk
输出分类关联规则Car
For (i=2;Fi-1≠∅;i++) Do
Ck←Car-candidate-gen(Fi-1);
Foreachfrequentitemsetf∈FkDo
Foreachcandidatec∈CkDo
Ifc.classsetiscontainedinfThen
c.classsupCount++;
Iff.class=c.classThen
c.rulesupCount++;
End for
End for
Cark←{f|f∈Fk,f.rulesupCount/f.classsupCount≥minconf};
End for
Return ∪Cark
4 实验评估
实验采用公开的临床数据集:加州大学欧文分校慢性肾病(Chronic Kidney Disease,CKD)数据集和皮肤病(Dermatology)数据集。考虑到数据集具有一定程度的缺失度,因此采用均值插值的方法对缺失值进行插值,并对连续属性项进行离散化分类处理。挖掘个人健康数据之间隐式关系、频繁项集、及分类关联规则模式。
慢性肾病数据集中有400个观测值,每个样本有25个属性项,其中14个是线性值类别属性项,11个是连续数值属性项,目标类是二元指示器,表征患者是否患有慢性肾病(ckd表示患有慢性肾病,notckd表示不患有慢性肾病)。皮肤病数据集中有366个观测值,每个样本具有35个属性项。其中,34个是线性类别属性项,1个年龄属性是连续属性项,目标类为6种可能的疾病类型。
4.1 数据预处理
实验中,当对年龄区间进行离散化时,遇到的问题是如何确定区间的宽度。如果区间过宽,会因为缺乏置信度而丢失部分关联模式;如果区间过窄,会因为缺乏支持度而丢失部分关联模式;如果区间宽度定为10岁,将会导致某些置信度低于阈值,或者某些支持度低于阈值。因此,研究采用分位数离散化(Quantile Discretizer)将连续型数据转换成分类型数据。
对于连续属性项类别数目,研究中是依据已有特征属性项目的分类的最大值确定。因此采用6个类别来划分各属性值,详见表1。例如,年龄属性([2, 90])通过字典序排序后,取用户数目的6个百分位数分成6个区间,即{(2, 34], (34, 46], (46, 54], (54, 60], (60, 67], (67, 90]},确保转换后的年龄特征的类别平衡性。
实验使用的皮肤病数据集见表2,年龄属性项采用6个类别进行离散化处理,即(0, 21], (21, 29], (29, 36], (36, 43], (43, 52], (52, 75],确保转换后的年龄特征的类别平衡性。

表1 实验所使用的慢性肾病数据集

表2 实验所使用的皮肤病数据集
4.2 CKD数据集频繁项集及关联规则挖掘
研究设定数据集中最后一列为目标类(ckd=患病,notckd=未患病),也就是分类关联规则的后件,实验的最小支持度minsup=0.15,最小置信度minconf=0.6,挖掘出最大的频繁k=13项集数量为3个,由此产生的关联规则模式见表3(截取前6个强关联规则模式)。
表3 CKD数据集关联规则模式
Tab. 3 Association rule patterns for chronic kidney disease data sets

分类关联规则模式支持度置信度高血压=yes=>class=ckd0.367 51糖尿病=yes·==>·class=ckd0.342 51细菌域=notpresent·高血压=yes·==>·class=ckd0.337 51脓细胞团=notpresent·高血压=yes·==>·class=ckd0.300 01高血压=yes·冠心病=no·==>·class=ckd0.292 51脓细胞团=notpresent·糖尿病=yes·==>·class=ckd0.282 51
由表3可知,当用户患有高血压疾病时,患有慢性肾病的支持度为36.75%,置信度为1;当用户患有糖尿病时,患有慢性肾病的支持度为34.25%,置信度为1;当这两种疾病与其它个人健康数据状况并发发生时,支持度略有下降。关联规则模式中另外一条记录(高血压=yes 糖尿病=yes ==> class=ckdsup:0.265conf:1),表示同时患有高血压和糖尿病的患者罹患慢性肾病的样例共有106例,置信度为1。此实验的研究结果与慢性肾病权威机构NIDDK提出的影响因素完全吻合[10]。因此,如果一名患者满足上述条件,那么该患者就有极大的可能性发展成为慢性肾病,对个人健康的影响风险巨大。针对此情况,患者要做好预防慢性肾病的准备。通过对分类关联规则模式和规律的分析,就可以挖掘有意义的信息来评价患者的身体状况。通过研究结果,最终揭示慢性肾病致病因素与个人健康数据状况的关联关系,要控制并发症的产生,防止疾病进一步恶化的情况出现,使患者能够及时接受治疗,为用户健康提供科学的服务推荐方法。
4.3 皮肤病数据集频繁项集及关联规则挖掘
研究中,设定数据集中最后一列为目标类(银屑病=1,皮脂性皮炎=2,扁平苔藓=3,玫瑰糠疹=4,慢性皮炎=5,毛发红糠疹=6),即关联规则的后件,本文中实验的最小支持度minsup=0.15,最小置信度minconf=0.6,挖掘出最大的频繁k=14项集数量为1个,由此产生的关联规则模式见表4。截取6个强关联规则模式,其中2个分类关联规则模式的目标类为“皮脂性皮炎=2”和“扁平苔藓=3”。

表4 皮肤病数据集关联规则模式
由实验可知,银屑病(class=1)的关联规则模式数量远大于其它类型皮肤病关联规则模式的数量。以表4中第一条数据为例,若某个皮肤病患者的临床症状满足“多边形丘疹=0,乳头状真皮纤维化=0,胞吐=0,海绵水肿=0,滤泡性角插头=0”,那么该患者的皮肤病类型为银屑病的支持度为25.41%,置信度为1。因此,如果一名皮肤病患者满足上述条件,那么就有极大的可能性是患有银屑病类型的皮肤病,医生会根据银屑病的临床症状与疾病特点,对患者对症下药。通过对皮肤病关联规则模式和规律的分析,可以挖掘出有意义的数据信息来对患者所属的皮肤病类别加以区分,针对疾病的特点进行治疗,为患者提供个性化的服务推荐方法。
4.4 算法性能评估
本节将讨论算法的性能。首先研究在不同最小支持度和最小置信度下的算法运行时间,如图2所示。2个数据集实验结果显示,最小置信度的变化对运行时间的性能影响不大,但是当最小支持度变小时运行时间会呈指数级增长。
对于构建的关联规则数量,如图3所示,关联规则的数量与运行时间的情况类似,都是随着最小支持度的降低,而呈现指数级的增长。
频繁项集的数量,只与最小支持度有关,与最小置信度无关,如图4所示。频繁项集的数量也是随着最小支持度的降低成指数级增长。这些实验结果表明,最小支持度,也就是项集的反单调性,对剔除非频繁项集是非常有效的。

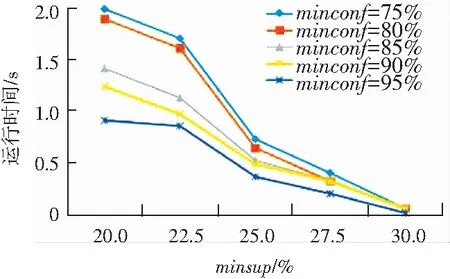
图2 不同最小支持度和最小置信度的运行时间
Fig. 2 Running time with different minimum support and minimum confidence
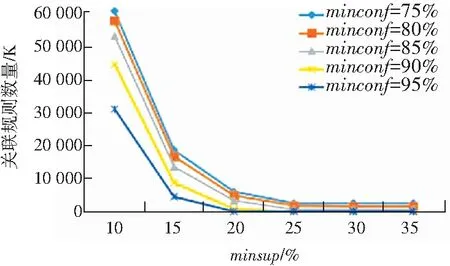
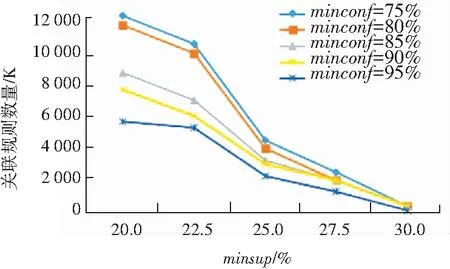
图3 不同最小支持度和最小置信度的关联规则数量
Fig. 3 Number of association rules with different minimum support and minimum confidence

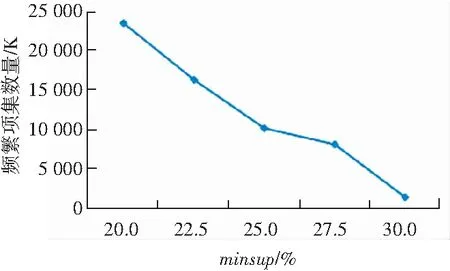
图4 不同最小支持度的频繁项集数量
Fig. 4 Number of frequent itemsets with different minimum supports
综上所述,如果最小支持度minsup较高,比如达到30%,此时就可以用较短的运行时间获得较少而有意义的关联规则,当然其中的很多规则可能是平凡的。如果为了挖掘更有意义的关联规则模式,可以采用较小的最小支持度,但这会导致无法接受的系统运行时间和指数级关联规则和频繁项集。因此采用合理的、可接受的最小支持度和最小置信度的值,是非常必要的。
5 结束语
本文提出从数据的隐式特征中识别出数据间的分类关联规则模式,通过支持度和置信度的权衡保证分类关联规则模式的有效性。基于关联分析的算法,对数据内在特征的分类关联规则模式进行挖掘,实现了个人健康数据的分解及分类,挖掘出数据的频繁项集,发现致病因素的重要数据特征,对个人健康特征的疾病预防与推荐具有重要的指导和建设性意义。
