分数阶RLβCα带阻滤波电路特性研究

周 瑞,李梦珑,2,胡国珍,章 磊,关若飞

(1.湖北理工学院 电气与电子信息工程学院, 湖北 黄石 435003; 2.武汉科技大学 机械自动化学院,武汉 430081)

0 引 言

分数阶微积分理论由于长期缺少应用背景支撑而发展缓慢，没有得到较多的研究和关注。直到Mandelbort[1]指出，在自然界以及许多科学技术领域存在大量的分数维事实，分数阶微积分理论才得以迅速发展。21世纪，分数阶微积分建模方法和理论在混沌系统[2-3]、信号处理与控制[4-6]等诸多领域已有较大研究发现和进展，凸显了其独特优势和不可替代性，其理论和应用研究在国际上已成为一研究热点。

非线性电路理论方面，研究结果表明分数阶微积分建立的实际电容和实际电感的数学模型更能准确地反映其电特性，分数阶的电容器与电感器相继被制造出来，充分说明实际电感与电容元件的分数阶本质特性[7-9]。目前，分数阶非线性电路理论已取得初步研究成果[10-15]。但是，RLC滤波电路其中作为一重要带阻滤波电路模型，分数阶下电路特性与滤波性能仍尚待进一步研究。

本文将RLC带阻滤波电路拓展至分数阶领域，利用分数阶微积分理论，建立新的分数阶滤波电路模型，对其新的电路特性和滤波性能进行系统的理论演绎分析和数值仿真研究。

1 阻抗特性

由图1，根据分数阶电路理论，易知分数阶RLβCα带阻滤波电路阻抗表达式：

(1)

进一步，阻抗模

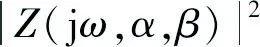
(2)

图1 分数阶RLβCα带阻滤波电路结构图

由式(2)，很难直观获得分数阶阶次α、β等系统参数对分数阶滤波电路影响规律。因此，给出如图2、3仿真实验结果。

观察图2(a)，随分数阶阶次α增大，分数阶滤波电路阻抗先缓慢增大，后迅速减小;当且仅当α=2时，阻抗值取最小;当α<1.5时，α对阻抗影响微乎其微。观察图2(b)，阻抗随分数阶阶次β增大迅速增大，即较小β可获得较小的阻抗值。此外，阻抗随频率f增大而增大。

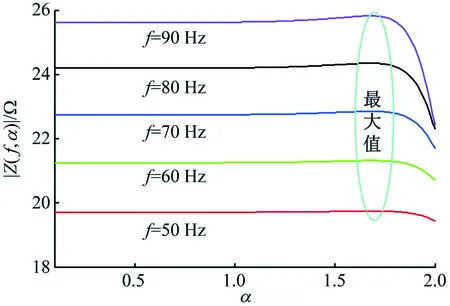
(a) β=0.8

(b) α=0.8

(a) C=0.1 μF

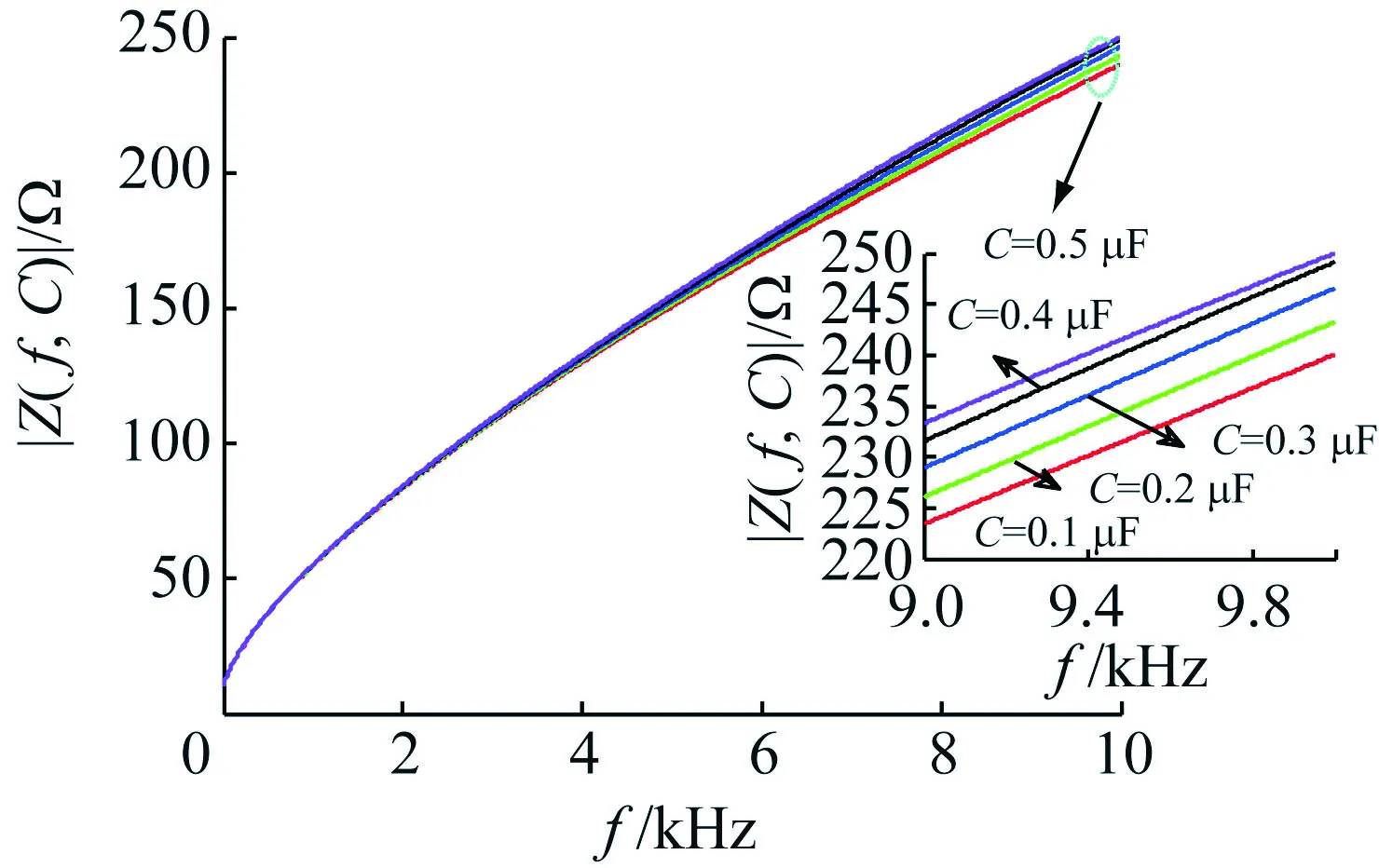
(b) L=0.1H

由图3，分数阶滤波电路阻抗随L及C增大而增大，即阻抗与L、C具有正相关性。

2 阻抗灵敏度

据上分析，系统参数对阻抗影响程度大小不一。因此，非常有必要进一步探究电路阻抗值对系统各参数灵敏度变化规律。一方面，通过选择高灵敏度系统参数可迅速获得理想电路阻抗; 另一方面，电路阻抗优化也可通过高灵敏度系统参数选取迅速获得。

根据相对灵敏度定义，可得:

(3)

图4中α、β中心阶次分别为0.7，0.8。对比观察，随分数阶阶次增大，阻抗灵敏度逐渐增大，且分数阶滤波电路阻抗对β具有更大灵敏度值，该结论与图2相互印证。

由图5可知，分数阶滤波电路阻抗对电感值L具有更高灵敏度，与图3所得结论一致。

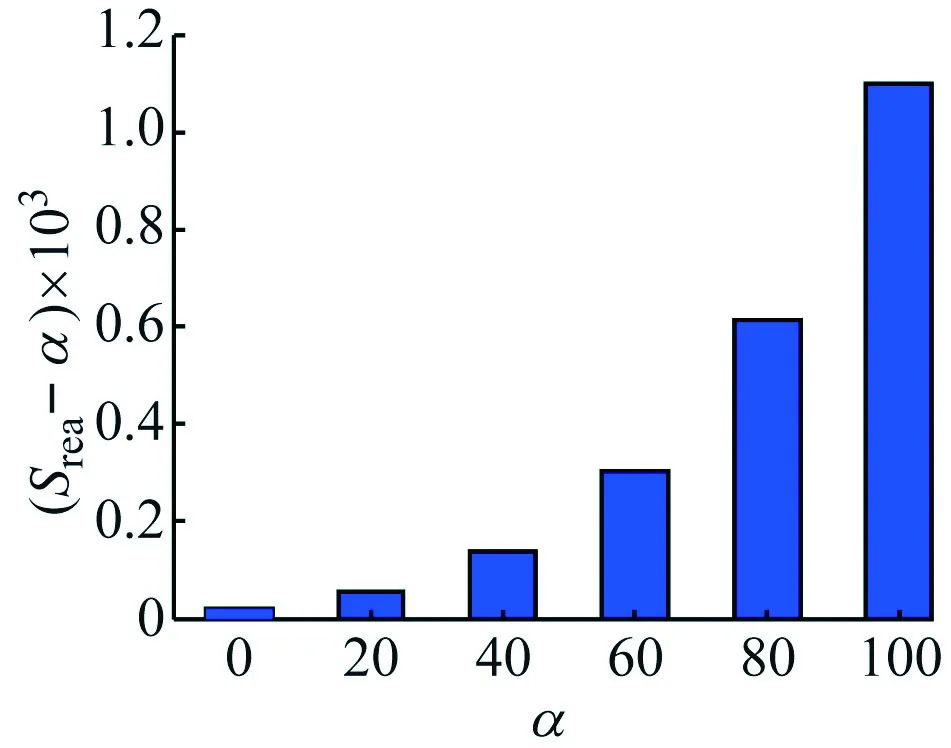
(a) β=0.8

(b) α=0.7

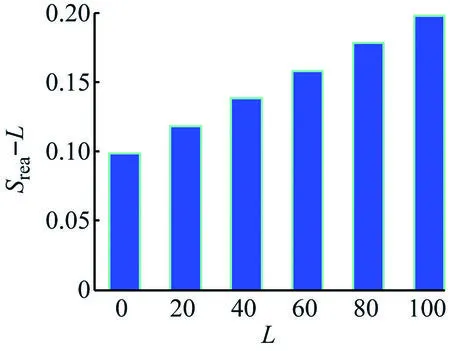
(a) C=0.1 μF

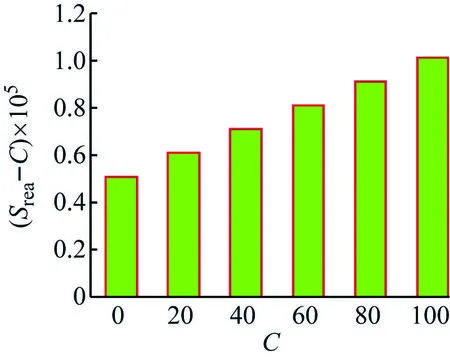
(b) L=0.1H

综上说明，分数阶RLβCα带阻滤波电路阻抗对β、L具有更高灵敏度，即通过调整β、L可很容易获得理想分数阶滤波电路阻抗。

3 幅频特性

由图6知，分数阶带阻滤波电路传递函数为

(4)

因此，可得其幅频响应为

(5)

对比图7和表1可知，α对低截止频率几乎无影响。随α增大，RLβCα带阻滤波电路谐振频率f0逐渐减小，带阻宽度BW逐渐减小，说明滤波电路分辨力越来越强。此外，滤波电路品质因数Q逐渐增大，说明其频率选择性越强。根据Q与阻尼系数ξ代数关系，ξ越来越小，表明滤波电路能量衰耗也会随α增大而减小。综上所述，较大α可增大滤波电路频率选择性，减小其电路能量衰耗。

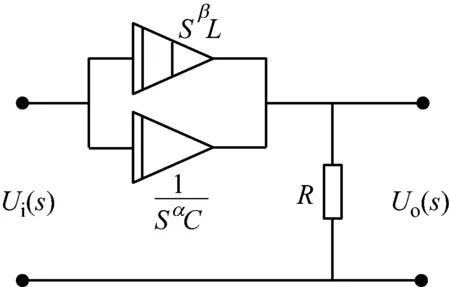
图6 分数阶RLβCα带阻滤波电路输入输出关系图

分析图8和表2易知，β对高截止频率无影响。随着β逐渐增大，分数阶带阻滤波电路谐振频率逐渐增大，而带阻宽度变化微乎其微，表明β对滤波电路分辨力影响很小。此外，品质因数逐渐减小，阻尼系数逐渐增大。因此，较小的β可增强滤波电路频率选择性，减小其能量损耗。

图7 不同α下，RLβCα带阻滤波电路幅频特性变化规律(L=0.1H，C=0.1 μF，R=10 Ω)

表1 不同α下，滤波电路性能参数表

β=0.8α=0.7α=0.9α=1.0α=1.3α=1.5低截止频率fL/Hz34.2734.2734.2734.2734.23高截止频率fH/Hz1.12×1088.81×1051.60×1054.81×1031096谐振频率f0/Hz6.20×1045.49×1032.34×103406.00193.80带阻宽度BW/Hz1.12×1088.81×1051.60×1054775.731061.77品质因数Q5.54×10-46.23×10-31.46×10-28.50×10-20.18阻尼系数ξ1.81×103160.5168.4911.765.56

图8 不同β下，RLβCα带阻滤波电路幅频特性变化规律(L=0.1H，C=0.1 μF，R=10 Ω)

表2 不同β下，滤波电路性能参数表

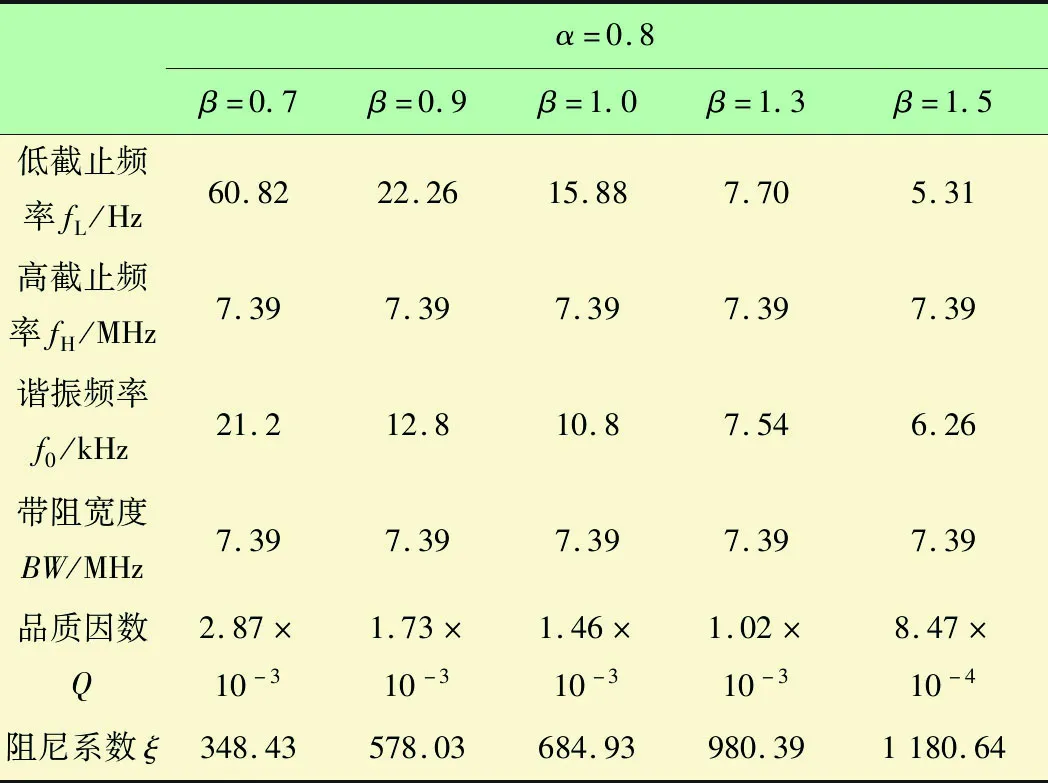
α=0.8β=0.7β=0.9β=1.0β=1.3β=1.5低截止频率fL/Hz60.8222.2615.887.705.31高截止频率fH/MHz7.397.397.397.397.39谐振频率f0/kHz21.212.810.87.546.26带阻宽度BW/MHz7.397.397.397.397.39品质因数Q2.87×10-31.73×10-31.46×10-31.02×10-38.47×10-4阻尼系数ξ348.43578.03684.93980.391180.64

同样，为了更好地探究系统参数L与C对RLβCα带阻滤波电路幅频特性影响，给出图9。

(a) C=0.1 μF

(b) L=0.1H

对比图9(a)与图8，显然，L与β对RLβCα带阻滤波电路幅频特性具有相同影响规律，即较小的L可增强滤波电路频率选择性。对比图9(b)与图7，C与α对分数阶滤波电路具有相同影响规律，即较大的α可增大滤波电路频率选择性。

4 相频特性

观察图10(a)，β、α对滤波电路相频特性有决定性影响作用，即随着β增大，滤波电路滞后相位差逐渐减小。分析图10(b)，相对而言，L对滤波电路相频特性有决定性作用，且随着L增大，滤波电路滞后相位差逐渐减小。

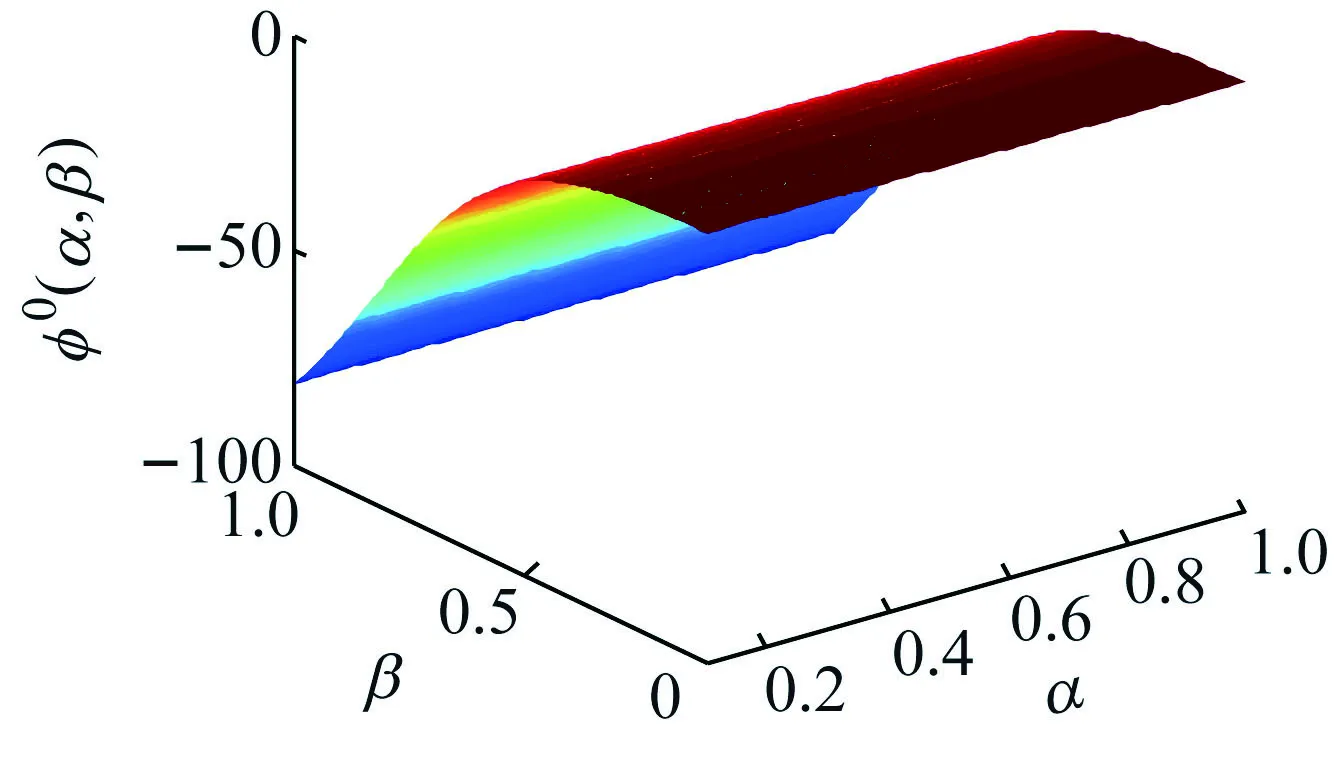
(a) L=0.1H，C=0.1 μF

(b) α=0.8，β=0.5

5 结 语

非线性RLC电路作为一重要带阻滤波电路，本文将其拓展至分数阶域，尝试探究分数阶RLC带阻滤波电路新特性与规律。分数阶阶次β与电感值L对分数阶RLβCα带阻滤波电路阻抗具有绝对性主导作用;较小β与L、较大α与C可优化滤波电路性能。研究结果表明，分数阶RLβCα带阻滤波电路在电路设计与分析方面具有更多可能性和自由度，不仅丰富了分数阶电路理论，而且为电路优化设计提供了理论支撑。