分布式能源用垂直轴风力机的结构优化设计

李 争，齐伟强，于潇雪

（河北科技大学电气工程学院，河北 石家庄 050018）

1 引言

随着科学技术的快速发展和对电能需求量的不断提高，新能源发电技术被逐渐提上日程，而风能发电在新能源发电中占有很大比例，因此研究具有更高发电效率的风力机迫在眉睫。风力机按照风轮轴的方向可分为水平轴风力机和垂直轴风力机。一般地，风轮轴平行于来流方向的风力机称为水平轴风力机，风轮轴垂直于来流方向的风力机称为垂直轴风力机。风力机按驱动原理又可分为升力型和阻力型两种。升力型垂直轴风力机起动转矩很高，在低风速下不易自起动；而阻力型垂直轴风力机可以低风速自起动[1-4]。

所研究的是一种新型垂直轴阻力型风力机。该风力机以塞内加尔式风力机为原型，其特点是起动性能好，在低风速下很容易起动，并且可以接受来自任何方向的风流，不需要对风，不需要安装偏航装置，易于维护、噪声低等。

与水平轴风力机相比，垂直轴风力机的大部分理论还在雏形阶段，还不能广泛应用于日常生活和生产中，其研究空间还很大。文献[1]分别对不同直径比的组合型垂直轴风力机气动特性进行仿真分析，得出了组合型垂直轴风力机的最佳直径比，在此直径比下与直线翼非组合垂直轴风力机对比发现组合型风力机风能利用系数与平均起动转矩有明显的提高；文献[2]提出了一种基于遗传算法的数值流程优化器可以对不同的叶片结构进行优化设计，并且通过仿真计算得出了可行性结果，改善了传统优化设计方法的效率；文献[3]应用流体仿真软件ANSYS CFX和FLUENT等对风轮水平放置的新结构的阻力型风力机进行优化分析，验证了风轮叶片结构与来流角度对风力机的性能有很大影响，最终得到最优模型；文献[4]设计了一种小型回旋式阻力S型垂直轴风力机模型，并给出了功率计算的一般方法和公式，具有普遍性的应用意义。

通过流体动力学仿真计算（CFD），对一种新型结构的阻力型垂直轴风力机的结构进行了新的探索，提出了垂直轴风力机的优化结构。通过应用ANSYS CFX空气动力学仿真软件对不同结构的风轮进行仿真计算，确定最优风轮结构。

2 小型垂直轴风力机模型与基本理论

2.1 风力机三维建模

小型垂直轴风力机模型，如图1所示。主要由风轮、液质悬浮式发电机、塔架、底座和控制及变换电路组成。风轮主要由连接盘和叶片组成，而叶片是由流线型直板和一半圆形弯板组成。通过连接盘将叶片分为两层，每层的三个叶片彼此相差120°排列，且两层之间错开60°。风轮高2m，半径0.5m，风力机总高度4.5m。

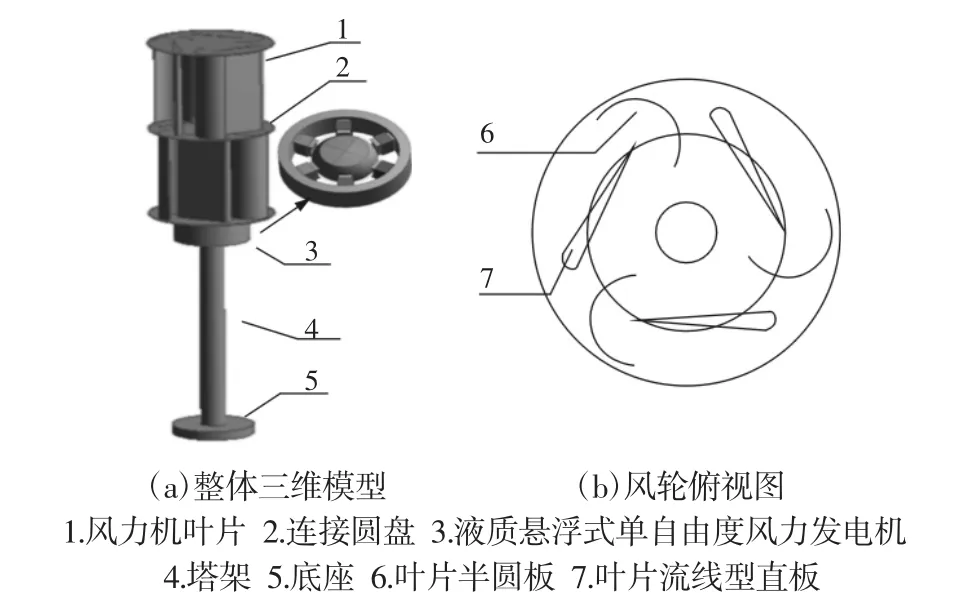
图1 垂直轴风力机模型Fig.1 VAWT Models

2.2 计算流体力学（CFD）的研究方法

计算流体力学（CFD）是建立在N-S方程近似解基础上的计算方法，根据近似解的精度等级，N-S方程的解法可分为线性非黏性流法、非线性非黏性流法、平均雷诺数的N-S方程法和全N-S方程法[5]。CFD数值方法包括有限元法（FEM）、有限差分法（FDM）和边界体积法（BIM）等[6-8]。FEM法精确度高，对已有程序使用方便，计算量大，适用于边界形状较复杂的场合。FDM法是最基本的标准解法。BIM法输入数据少，适用于定长流中的流体自由表面流。综合考虑，选用有限元法（FEM）。

2.3 基本理论公式

（1）尖速比λ指风轮叶尖线速度与风流速度之比，是衡量风力机性能的一个重要参数。其表达式为：

式中：R—风轮半径m；ω—风轮角速度rad/s；V—来流速度m/s。

（2）风能利用系数Cp指风轮能够吸收风能的多少，又称为风力机转换效率，是衡量风力机性能的又一个重要参数。其表达式为：

式中：T—风力机转矩Nm；ρ—空气密度，取1.185kg/m3；A—风力机的扫掠面积m2。

（3）转矩系数Ct表达式为：

式中：D—风轮直径m。

（4）风轮实度δ指风力机叶片的投影面积所占风力机面积的比值，也是风力机的一个重要参数。其表达式为：

式中：B—叶片个数；C—叶片弦长m；R—风轮半径m.

（5）翼型的升力与阻力

当有风吹来时，置于空气中的翼型将受到力的作用F，将其分解，可得与风向平行的阻力（D）和与风向垂直的升力（L）；表达式如下：

式中：cL—与升力相对应的系数；cD—与阻力相对应的系数；c—与总动力相对应的系数；A—各个力及叶片在来流方位上的影面积 m2；ρ—空气密度 kg/m3；v—来流速度 m/s。

2.4 层流与湍流

为了区分层流与湍流，引入雷诺数Re的概念，其表达式为：

式中：ρ—流体密度 kg/m3；V—来流速度 m/s；D—管道直径 m；μ—动力黏性系数kg/（m·s）；

当雷诺数Re大于上临界雷诺数时，属于湍流流动；小于下临界雷诺数时，属于层流流动；介于上下临界雷诺数之间时，属于过渡状态[9-11]。在实际工程应用中，取临界雷诺数为2300。湍流流动复杂，在实际中需要附加湍流方程[12]，此处选用标准k-ε模型方程，其表达式为：

湍动能k方程：

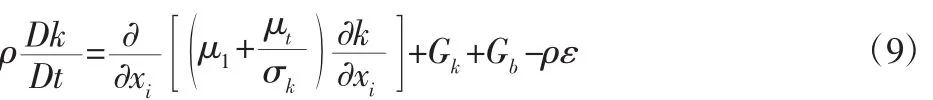
耗散率ε方程：

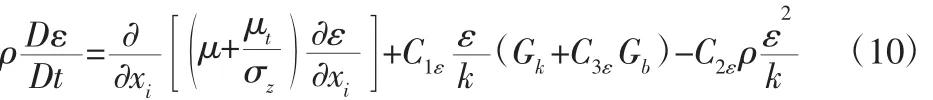
式中：μI—层流粘性系数；μt—湍流粘性系数；Gk—由层流速度梯度而产生的湍流动能；Gb—由浮力产生的湍流动能。一般取C1ε=1.44Gk，C2ε=1.92，C3ε=0.09，σk=1.0，σε=1.3。

3 网格的无关性验证及风力机基本特性

3.1 网格无关性

在有限元分析中，网格的划分形式多种多样，主要可以分为自动网格划分、四面体网格划分、六面体网格划分、扫掠网格划分、多域网格划分和cut cell网格划分六种形式[13-15]。由于本三维模型的复杂性和特殊性，只有使用自动网格划分、四面体网格划分、六面体网格划分才能使得求解收敛。但采用四面体网格和六面体网格划分方法求解复杂、耗费时间长和计算精度低等缺点，因此采用了自动网格划分方法。该方法的优点是具有很好的智能性，在形状规则的区域网格数目少、体积大，在形状复杂的区域网格数目多、体积小。另外，它也是系统默认的网格划分方法。其自动网格和六面体网格划分形式，如图2（a）～图2（c）所示。

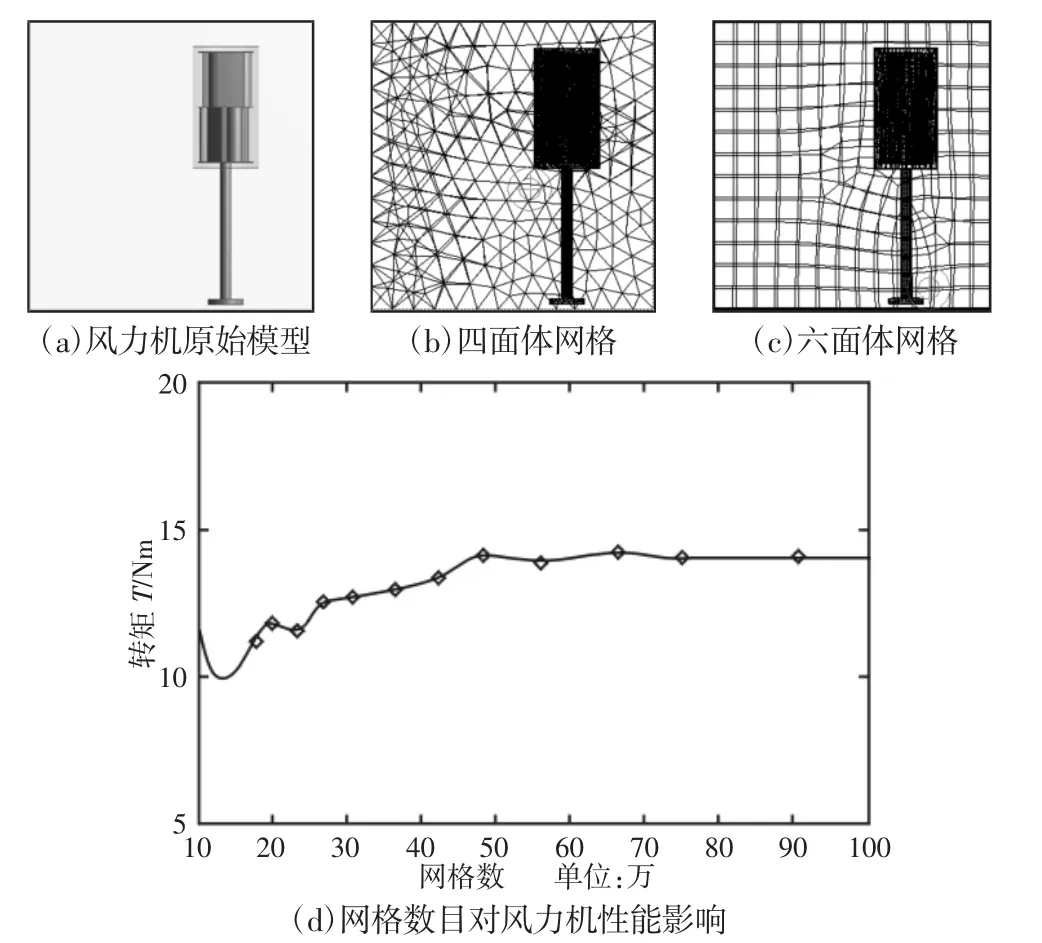
图2 网格无关性验证Fig.2 Mesh Independence Verification

为了进行网格无关性验证，采用默认的自动网格划分形式。通过改变网格数量，查看风力机的转矩T变化情况，如图2（d）所示。从图中可以看出，随着网格数量的增加，风力机的转矩大体上呈增大趋势。但当网格数达到48万左右时，转矩T基本不在变化，成一恒定值14Nm。因此，模型是在网格数目设定为48万时进行计算求解的。

3.2 风力机的基本特性

由式（1）～式（3）可知，风能利用系数和转矩系数是衡量风力机优劣的重要参数，直接影响着风力机的效率，因此，研究风能利用系数或转矩系数随风速和风轮角速度的变化规律显得十分重要。风能利用系数Cp随叶尖速比λ的变化规律，如图3（a）所示。求解过程中保持风速v=10m/s，任意调整风轮角速度为不同值，使得叶尖速比λ在（0～1）之间变化。由图可以看出，风能利用系数随叶尖速比的增加先增加后减小，且在叶尖速比λ为0.5左右时，风能利用系数Cp达到最大值，此时的风力机的风轮效率最高。风力机的转矩系数Ct随叶尖速比λ的变化规律，如图3（b）所示。可以发现，转矩系数基本上随叶尖速比的增加而增加，并且具有很小的非线性[3]。

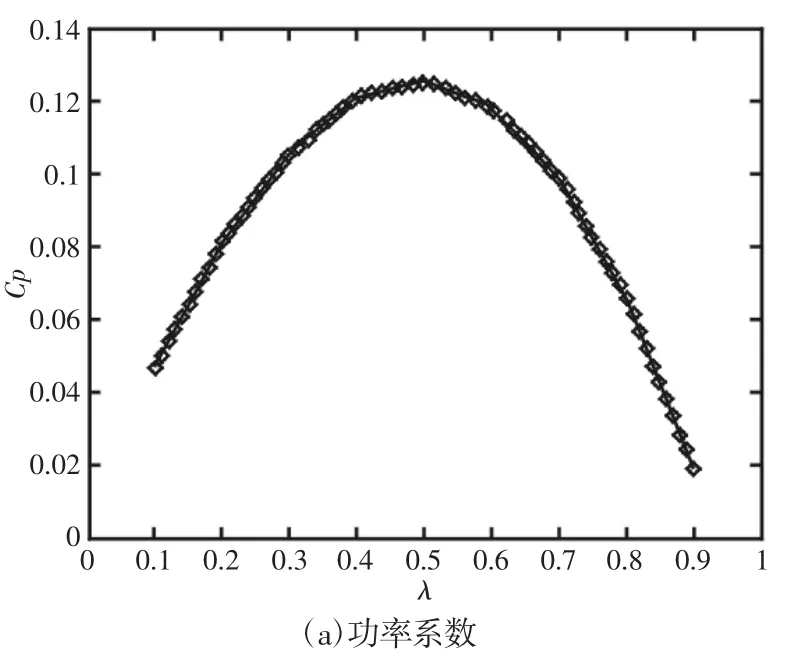
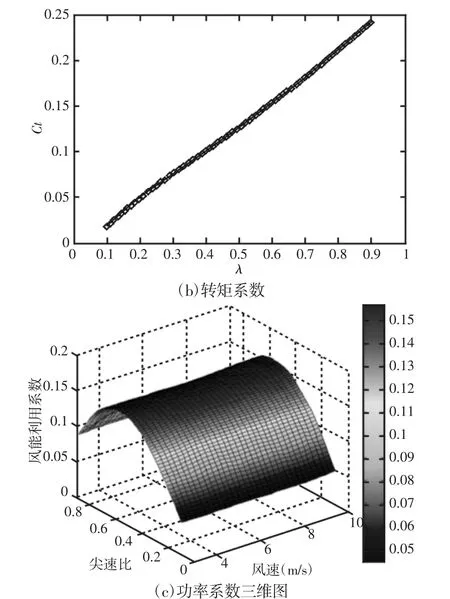
图3 垂直轴风力机基本参数曲线图Fig.3 Basic Parameter Curve of VAWT

为更好地表达风力机的特性，对风能利用系数做了更进一步的研究。设定风流速度 v 分别为 3m/s、5m/s、7m/s、9m/s、10m/s时，风能利用系数随叶尖速比的变化规律基本上都与图3（a）的变化规律相近。最终将该变化规律推广，得到风流速度v为（3～10）m/s时，风能利用系数随叶尖速比与风流速度的三维变化规律，如图3（c）所示。从图中可以看出，当风流速度v为（3～10）m/s任意一值时，风能利用系数与叶尖速比都呈现这种抛物线规律，并且数值也基本不变。在此印证了风能利用系数是风力机的固有参数，它不随外界因素的改变而改变，风力机一旦生产制造，结构参数便已固定，因此风力机的风能利用系数也是一定的。

4 计算结果分析

4.1 风力机叶片形状的优化

垂直轴风力机是捕获风能的旋转机械，风轮系统是风力机的重要组成部分，直接影响着风力机的优劣。风力机的叶片为典型的阻力型叶片，在此从改变风力机叶片的结构着手，验证风力机的优越性，如图4（a）所示。此四种结构都是改变风力机叶片的直板来研究的，结构a为无直板，即叶片只是有三个半圆板组成；结构b为直板长度0.3m，即叶片由短直板与半圆板组成；结构c为直板长度0.5m，即叶片由长直板与半圆板组成；结构d改变直板为流线型，即叶片由流线型直板与半圆板组成；将四种叶片结构分别进行仿真计算，设定来流风速为10m/s。

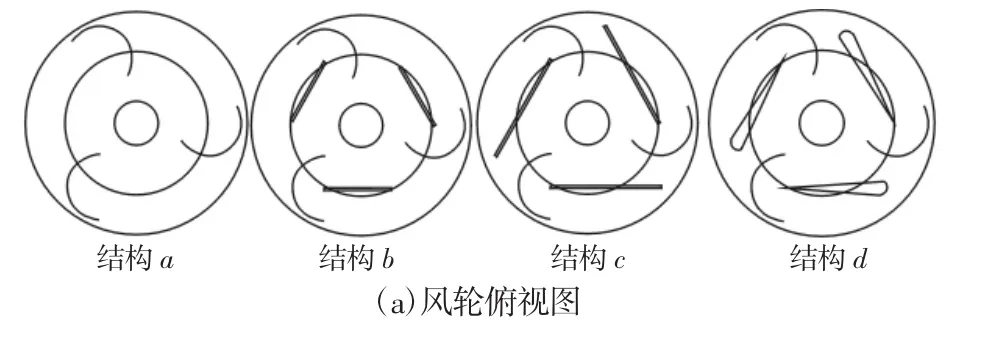
图4 四种风轮的性能对比Fig.4 Performance Comparison of Four Turbines

四种结构的风能利用系数对比图，如图4（b）所示，由图中可知，结构a风能利用系数最低，结构d的最高，为最优结构，而结构b和结构c的风能利用系数相差不大；另一方面，结构a和结构b达到最大风能利用时，对应的叶尖速比为0.4，而结构c和结构d达到最大风能利用时的叶尖速比分别为0.5和0.6。此外a、b、c、d四种结构的曲线所包含的的叶尖速比范围也依次变大。综上所述，无直板结构的风能利用系数曲线完全被短直板结构所包络，并且最佳叶尖速比没有后移；长直板相对于短直板来说，最佳叶尖速比发生后移；流线型直板结构完全将其他三种结构包络，且最佳叶尖速比相对于长直板结构又有一定的后移。因此，所采用的流线型直板加半圆板的叶片结构能更好的利用风能，为最优结构。

4.2 叶片中间加小挡板结构优化

叶片是决定垂直轴风力机性能的重要部分，为了使风力机能够高效的利用风能，达到更好的发电效果，因此对叶片结构的研究至关重要[16-17]。在此对中间加有小挡板的叶片进行对比分析，讨论该做法是否可以更好的优化风力机，使它能更好的利用风能。风力机的三种叶片结构，如图5（a）所示。结构a为不加小挡板时的原始叶片结构；结构b为加一片小挡板时的叶片结构；结构c为加两片小挡板时的叶片结构。

图5 加小挡板的结构优化Fig.5 Structural Optimization with Damped Plates

对以上三种结构的风力机叶片分别进行仿真分析，设定来流风速为10m/s，边界为速度入口，零压力出口，其计算结果如图5（b）所示。从图中可以看出，不加小挡板时的原始结构a与加两片小挡板的结构c除在叶尖速比λ为（0.4～0.6）时不重合外，在其他的大部分区域上都基本重合，而加一片小挡板的结构b被另外两结构所包络，这说明风力机加一片小挡板使得其性能降低，加两片小挡板使得其性能又恢复到原始模型，因此如果考虑在风力机叶片中加小挡板，就要避免只加一片，至少要加两片或者更多。总之，小挡板对风力机的风能利用还是有一定作用的，随着小挡板数量的增加，风力机的风能利用有所提高，但这种改善不是很明显。在此所提到的风力机叶片模型采用不加小挡板的原始结构a。

4.3 叶片数对垂直轴风力机的影响

风力机叶片的形式多种多样，在生产和生活中的大部分水平轴风力机都采用三叶片结构，其优势为叶片流量大，噪声低，符合流体力学原理。且三叶片结构还具有较好的动平衡，不易产生振荡，减少轴承的磨损，从而降低了维修成本。这里分别给出叶片数为2叶片、3叶片和4叶片三种结构的小型垂直轴风力机形式，如图6（a）所示。进行流体动力学仿真计算，确定出最优叶片数，为垂直轴风力机的更深入研究打好基础。在此将每种结构的风力机在空间每隔10°旋转一次，旋转一周完成，分别计算风力机各个方向上的转矩变化，研究风力机在旋转一周内的转矩波动，从而推广到实际风力机风轮旋转时的转矩波动。设定风流速度v为10m/s，最佳叶尖速比λ为0.6，进行流体动力学仿真计算。

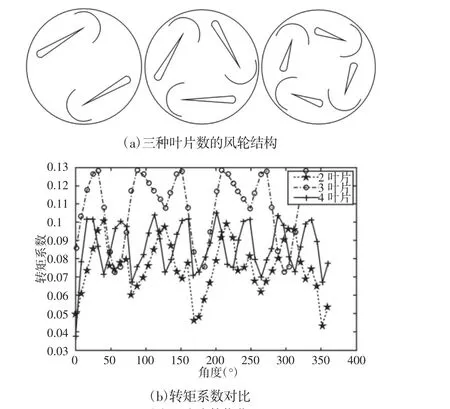
图6 叶片数优化Fig.6 Optimization of Blade Numbers

三种叶片数的流场计算结果，如图6（b）所示。从图中可以看出，2叶片结构风轮转矩波动最大，而且起动转矩也较低，不利于风轮的起动；3叶片结构风轮相对于2叶片的风轮除转矩波动有所减少之外，最主要的是其起动转矩较高。这样在相同的风流速度情况下，3叶片结构风轮更易起动；4叶片结构风轮虽然其转矩波动较小，但是其起动转矩也很小，不利于风力机的起动。它的起动转矩稍高于2叶片的起动转矩，却远远低于3叶片结构的起动转矩。通过转矩波动和起动转矩综合考虑可知，三叶片其转矩波结构最为合理。在此仅计算了风轮旋转一周的转矩情况，由一周推广到多周。不难发现，风轮旋转时转矩系数的普遍规律。

5 结论

针对一种新型的垂直轴风力机结构，通过流体动力学模拟平台进行整体仿真计算，对风力机的叶片等部件进行优化，得到了风力机风轮的最优结构。通过网格划分研究，验证了计算域的网格无关性，确定了网格数为48万左右时，对风力机的仿真计算结果更为准确；通过对风力机的基本特性的研究，得出了风力机的风能利用系数和转矩系数随叶尖速比的变化规律曲线，并将风能利用系数曲线推广到风流速度为（3～10）m/s时的更宽范围，且范围拓宽后的变换规律与某种特定风速下的变换规律相一致，从而得出风能利用系数是风力机固有参数，它不随外来风流速度的改变而改变；同时，对四种风力机叶片直板的结构进行对比分析，得出了当叶片直板为流线型时，风轮的风能利用最好的结论；最后探索了风力机叶片数目对转矩系数的影响，并进行了不同叶片数量下的对比分析，确定了最佳叶片数。