广东湖北碳排放权市场动态相依性分析与风险测度

杨 奕

（南京林业大学 经济管理学院，南京210037）

1 文献综述

作为一种金融创新的工具，碳排放权交易以市场机制敦促发达国家之间以及发展中国家之间以较低的成本，共同实现温室气体减排的最终目标。因此，研究碳排放权交易市场是十分有意义的。

对于碳排放权交易风险的研究，国内外研究主要是集中在欧盟碳排放权交易市场（EU ETS），欧盟市场作为目前全球最大也最成功的碳交易市场，吸引着许多学者注意。张跃军、魏一鸣（2011）根据投资组合理论测算了EU ETS 的系统性风险[1]。陈伟、宋维明、田园（2014） 运用GARCH 分析了欧盟市场和芝加哥气候交易所两个市场的在险值[2]。凤振华（2012）使用GARCHEVT-VaR 模型对欧盟市场的碳收益序列残差进行拟合分析，使用VaR 模型分析静态VaR 以及GARCH 模型分析动态VaR[3]。国内学者对我国碳排放权交易市场风险研究大多数是仅仅就碳排放交易现象本身做出思考拓展。赵黎明、张涵（2010）对我国碳排放权交易市场风险的类型做了浅显的分析，认为风险种类有政治风险、经济风险、法律风险、市场风险、操作风险、项目风险六大类[4]。朱德莉（2018）指出碳市场也存在交易成本、技术革新、环境绩效等风险[5]。这些研究缺乏有效实证作为基础，吴恒煜、胡根华运用Copula-GARCH模型研究了欧洲气候交易所CER和EUA现货市场和期货市场之间的动态相依性[6]。吕勇斌、邵律博（2015）通过GARCH 模型研究了我国碳交易价格波动的特征，发现各试点市场的碳交易价格的差异性较为明显[7]。刘用明、周飞、甘永春（2017）使用ARCH模型对北京碳排放权交易市场的流动性和价格波动性两方面对风险进行了度量[8]。郑祖婷、沈菲、郎鹏（2018）对深圳市场的交易数据进行实证检验，为我国碳市场交易价格波动提供风险预警的合理建[9]。对我国市场实证研究目前开始逐渐变多，但是大多数研究只针对于某个特定市场。

本文着重选择具有代表性的湖北、广东两个交易市场进行动态相依性与风险测量分析。本文运用GRACH模型、极值理论和Copula函数计算两个市场相关性和组合风险，这为碳排放权市场风险管理提供一定指导依据，相信能够帮助交易者在一定程度上降低风险，也帮助我国碳排放权市场更好应对风险。

2 计量模型

本文研究主要步骤如下：①使用非对称GARCH 模型即GJR-GARCH 模型对数据进行过滤进而提取残差；②使用广义Pareto分布即GDP估计方法来构建样本边际累积分布函数CDF 以及上下尾；③然后使用Copula 函数对提取的残差之间相关度进行分析；④最后利用Copula 函数评估我国碳市场风险价值VaR[10-12]。

2.1 过滤数据

在所有GARCH族模型里，一个形式最简单并且应用最广泛的一个模型就是GARCH(1，1)模型，其形式为：

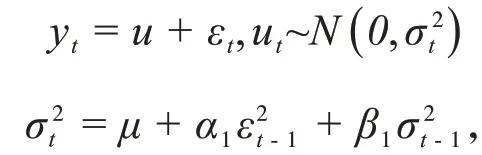
其中，yt表示收益率，u表示均值，εt表示随机扰动项，表示条件方差；参数μ，α1，β1都大于0 且α1+ β1＜1。第一个等式是均值方程，第二个等式是方差方程。

由于GJR-GARCH模型能够更好地刻画方差波动的非对称性，因此本文使用GJR-GARCH 模型，形式如下：

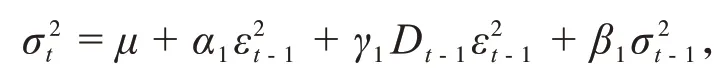
其中Dt-1为示性函数。

2.2 边缘分布

2.2.1 POT模型

广义极值分布可以用来对样本极大值进行拟合，但在实际情况中，往往因为需要数据样本量过大而难以实现，因此POT模型选择对超过某个阈值的所有数据进行建模。设X1，X2，…，Xn有相同的分布函数F(x)，则阈值满足条件τ＜ω(F) =sup{x:F(x) ＜1}。

2.2.2 广义Pareto分布

对某个阈值τ，超过阈值的变量Yi-τ 的分布函数为：

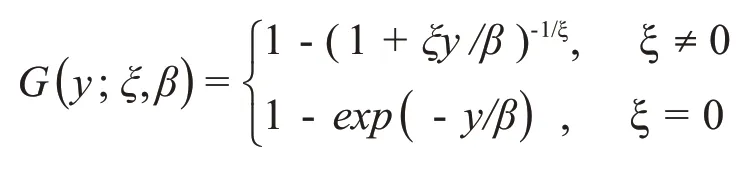
其中，ξ和β分别为形状参数以及尺度参数。金融领域中，相对常见的是ξ ＞0 的分布，此时分布尾部较厚，在拟合数据时效果较好，例如柯西分布以及t分布。

2.3 Copula函数

本文选用t-Copulɑ函数，若一个联合分布的边际分布为F1，…，Fn，存在一个Copulɑ函数，可以满足F1(x1，…，xn)=C(F1(x1)，…，FN(xn))。

2.4 VaR计算

本文运用极值理论和Copulɑ函数，通过对市场收益进行模拟回报，形成一个投资组合，获取组合对数收益率，并设定一定置信水平α，由分位数得到投资组合VɑR。

3 实证研究

3.1 数据选取

本文在中国碳交易网站上提取了从2015年7月27日至2019年4月30日的广东省以及湖北省两个市场日交易数据，每组样本都有917个数据。截止2018年底湖北市场碳排放交易额和交易量最多，广东市场碳排放交易额和交易量居中。收益率ri表示为：

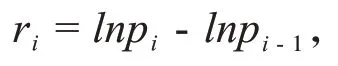
其中，pi为第i天收盘价。

因此，同样可以得到日对数收益率，每组916个数据。结果表明两个市场收盘价的波动是有很大起伏的，说明市场是比较活跃并且存在一定风险的。

3.1.1 收益率序列描述性统计

本文对广东市场以及湖北市场的日对数收益率进行描述性统计，并对统计量进行整理，如下表1所示。可以发现：

①从偏度数据看，广东、湖北两市场收益率均值小于0，也就是说明呈现左偏，说明两个市场收益率序列的分布具有不对称性，收益率高于平均收益率的天数比低于平均收益率的天数要少。

②从峰度数据看，两个市场收益率数据的峰度都超过了3，序列呈现“高瘦”形状，序列分布比正态分布更为集中。

③从JB统计量以及对应P-值看，可以发现两个市场的JB 统计量都是足够大的，并且广东、湖北两个市场对应P-值=0.000 000，可以认为两个市场的收益率序列都不服从正态分布。

3.1.2 收益率序列平稳性检验

在进行数据统计分析的基础上，由于大多数金融数据都是非平稳的，但为了减少回归过程中的伪回归问题，我们希望采用平稳数据，所以我们要对所研究数据平稳性进行检验。一般情况下，可以通过对序列的一些属性图进行粗略判断，但是这样方法是不够准确的，因此使用单位根检验方法。

从表2可以看出，两个市场ADF值都远小于边界值，P值是代表序列不是平稳序列的接受程度的概率，表中值为0，表明显著拒绝原假设，原序列没有单位根是平稳序列。因此，两个市场日收益率序列都是平稳的。

3.1.3 自相关检验

对广东市场对数收益率序列进行自相关和平方自相关检验，共序列存在轻微相关性；从日对数收益率平方自相关检验可知序列存在GARCH效应。

对湖北市场对数收益率序列进行自相关和平方自相关检验，序列存在轻微相关性；从日对数收益率平方自相关检验可知序列存在GARCH 效应。

3.2 数据过滤

通过以上对数据处理，可以发现广东和湖北市场都是呈现尖峰厚尾状态，序列平稳相关，存在GARCH 效应。因此，使用GJR-GARCH 模型，对数据进行过滤，提取过滤残差进行分析，可以得出，过滤残差及其标准差波动是有聚集性的，湖北市场过滤残差的波动性更大，波动的频率也更高。在对序列数据进行过滤得到残差之后，通过对应的条件标准偏差来对残差进行标准化，检查过滤残差及标准化残差的平方。

3.3 极值分布以及参数估计

3.3.1 估计半参数CDF

在上面数据中，得到了标准化残差，为了对残差进行更好的估计分布，将EVT 应用于残差的尾部，其余部分使用CDF。运用Matlab 进行编程，确定上下阈值，对尾部保留10%残差，运用峰值方法，得到CDF图。虽然前面图说明了复合CDF，但是对GPD 拟合效果会更好。本文采取绘制残差上尾超过的经验CDF 以及GPD 拟合。虽然只使用了10%的标准化残差，但拟合分布紧跟超标数据，因此GPD的拟合模型效果是不错的。

表1 两市场收益率序列描述性统计

3.3.2 Copula函数参数估计

本文运用Matlab编程得出t-Copula函数的相关系数矩阵，见表3。其中，t 分布的自由度为25.7637。

由此可见，广东市场和湖北市场之间的相依度较小。这种现象可能是我国市场的发展处于开始阶段，管理办法、统计部门、排放规模、MRV差异很大等原因导致的。但是广东市场和湖北市场之间的相依度较小，可以在一定程度上降低投资组合风险价值，从而有利于进行风险管理。

3.3.3 VaR计算

通过给定的copula参数本文模拟市场的回报并形成投资组合，在一个月的风险范围内，生成最大模拟增益以及最大模拟损失，并得到在不同置信水平下的VaR。

从表4中可以发现置信区间越小风险越小，说明投资者若是想要有效规避风险，应该尽早选择退出市场。此外相关系数可以间接反映投资组合风险价值VaR 大小，一般情况下，相关系数越小投资组合风险的VaR 值越小，因此由广东和湖北两个碳排放权市场构成的投资组合风险要小。

表2 两市场ADF检验结果

4 结论和建议

本文通过对我国试点碳排放权交易的广东市场和湖北市场的日收盘价以及收益率进行统计分析，有关结论如下：①运用Copula 函数进行市场相依度研究，两市场之间相关系数为0.0271，可以认为两市场之间的相依度较低；②运用广义极值模型、GJR-GARCH 模型和t -Copula 函数对我国市场风险进行测度，得出市场投资组合的风险价值VaR，发现置信区间越小风险越小。

2017 年我国建立全国统一的碳排放权交易市场，但从本文实证结果来看，要建立更加健全完善全国统一的碳交易市场仍然任重道远。本文由有以下几点政策建议：①通过统筹分配碳排放配额指标来尽可能消除各区域试点的差异，进而有助于整合成为全国统一的市场；②加快推进全国碳市场基础设施建设并优化碳排放数据报送系统，可以完善全国碳市场注册登记系统和交易系统；③通过营造一个良好的市场环境和完备的市场交易机制来提高市场有效性，这样更好地发挥市场在碳排放配置方面的作用；④逐步纳入更广泛的市场交易主体，进而能够增强市场流动性和市场活力。

表3 t-Copula函数的相关系数矩阵

表4 最大模拟增益和损失、VaR