基于柔度误差检测的锚杆台车机械臂定位

夏毅敏 马劼嵩 张亚洲 李正光 宁波

(1.中南大学 高性能复杂制造国家重点实验室 ∥ 机电工程学院，湖南 长沙 410083；2.中铁十四局集团大盾构工程有限公司，江苏 南京 211800；3.中国铁建重工集团有限公司，湖南 长沙 410100)

锚杆台车是一种集钻、装、注为一体的隧道施工设备。但传统的锚杆台车人工定位精度低且速度慢，对隧道施工效率和质量造成了严重的影响。实现锚杆台车的自动化施工能有效提高施工质量并保障工作人员的施工安全，而锚杆的快速准确定位是其中最关键的步骤。

现在大多数提高机器人定位精度的研究是通过机器人标定技术来实现的，而基于运动学模型的标定流程主要包含误差建模、误差测量、参数辨识以及误差补偿4个部分[1- 2]。目前国内外针对锚杆台车的相关研究主要集中在结构设计和工程应用方面，对锚杆定位研究较少，但同类工程机械的运动学研究主要包括机械臂误差补偿以及逆运动学求解。齐飞等[3]提出了通过运动学标定对定位误差进行补偿的方法；黄开启等[4]将钻臂形变等效为一个虚拟关节，推导出其形变误差模型。Hussein等[5]采用有限元法计算机器人连杆的变形。Jiang和Wang等[6- 7]在求凿岩台车的运动学逆解的过程中，改变关节输入条件，并且计算过程不涉及数值迭代和操纵矩阵；Wang等[8]在进行凿岩台车求逆解时利用对偶四元数法进行建模；周友行等[9]基于运动轨迹来求多关节冗余机器人运动学逆解。

上述研究对臂架的柔度误差多采用理论推导和仿真模拟来获得，而锚杆台车机械臂的工作空间大，同时作业部自重可达2.5吨，加之机械臂的低刚性，使其具有很大的变形量；其次由于制造及安装误差，臂架实际几何参数与设计参数之间存在偏差；各种理论或仿真计算的变形量往往存在较大误差，导致定位不准。因此，基于工业机器人运动学误差补偿研究[10- 18]，笔者采用DH法建立锚杆台车正向运动学模型，提出一种基于机器视觉和激光测距的柔度检测方法来获得臂架柔度误差，并通过全站仪计算参数误差，建立运动学误差补偿模型；在进行定位时，采用牛顿拉夫逊迭代法和梯度投影法，结合柔度误差和参数误差补偿模型，求两次逆解确定关节变量，以保证锚杆台车的定位精度。

1 锚杆台车简介

1.1 锚杆台车机械臂结构介绍

锚杆台车机械臂包括6个回转关节和2个移动关节，为八自由度冗余机器人，钎杆和锚杆单元安装在推进梁上。主要结构如图1所示。

1—大臂横摆关节(θ1)；2—大臂俯仰关节(θ2)；

1.2 锚杆定位方法

引起锚杆台车定位误差的主要原因是柔度误差和参数误差。柔度误差包括自重、外力等导致的弹性变形；参数误差包括结构参数误差、环境因素(温度、磨损)导致的尺寸误差和传感器误差等。

当给定末端位姿时，首先根据理想正向运动学模型求逆解；利用关节运动范围确定初始搜索值，同时为保证计算速度和精度，预先设定精度要求，通过迭代法和梯度投影算法对锚杆台车8个关节不断搜索，得到关节变量，并驱动机械臂运动到该位置；锁死前3个关节，利用柔度误差检测装置测量此时大臂的挠度变形值，获取测量位置的实时姿态，构建基于测量位置的末端位姿矩阵，以此补偿柔度误差。然后令后5个关节的关节变量作为求参数误差的输入值以及运动学误差补偿模型求逆解的初始搜索值，利用牛顿迭代法对后5个关节进行二次求解，使锚杆达到期望位姿。锚杆末端定位及各关节参数确定的优化程序如图2所示。

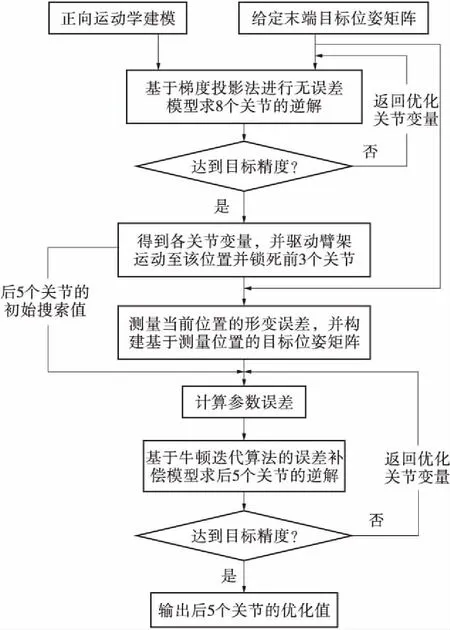
图2 优化程序

2 运动学误差补偿模型的建立

2.1 机械臂理想运动学模型

根据锚杆台车结构参数，建立各关节坐标系，机械臂DH参数如表1所示，建立的锚杆台车运动学模型如图3所示。

将参数代入坐标变换矩阵，即式(1)：

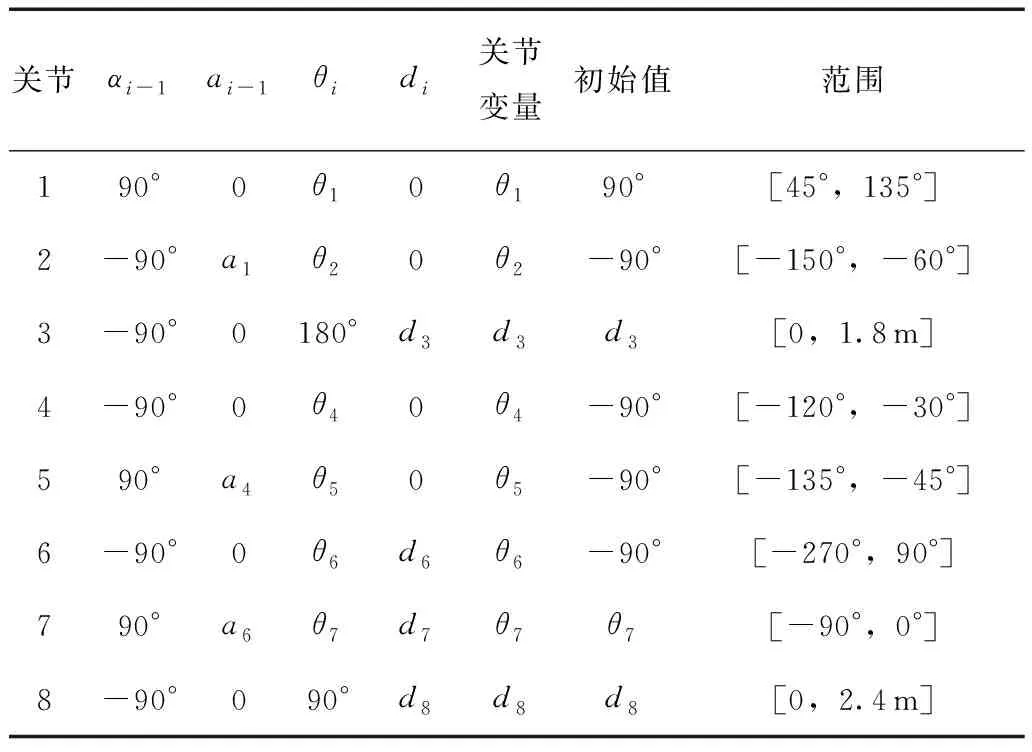
表1 机械臂DH参数表

(1)

式中：i表示第i个关节，C(θi)=cosθi，S(θi)=sinθi；ai-1为连杆长度；αi-1为连杆转角；di为连杆偏距；θi为关节角。

得到锚杆台车正向运动学模型如式(2)所示：

(2)

式中：P=[px，py，pz]，为锚杆位置矩阵，px、py、pz分别表示锚杆在基坐标系中的位置；R=[n，o，a]为锚杆的姿态矩阵，n、o、a分别表示锚杆在基坐标系中的方向矢量。

2.2 基于机器视觉的臂架柔度误差检测

2.2.1 测量原理

锚杆台车机械臂的大尺度和低刚性是其不同于传统机器人的典型特征，特别是大臂伸缩关节的柔度变形是导致定位精度低下的最主要原因。因此可以将臂架分为两个部分：第1部分是1、2关节；第2 部分是4-8关节组成的5自由度机械臂。这两部分刚性相对较大，而大臂伸缩关节的柔度误差采用现场自动测量的方法确定。

测量原理如图4所示，在动臂末端安装一个标靶，标靶垂直于动臂横截面，与标靶固定连接一个工业相机，采集并计算图像信息获得光斑在标靶上的二维坐标，如图5所示。于大臂根部安装一个激光测距仪，使光束平行于大臂轴线。在标靶底部装有双轴倾角传感器，测量标靶姿态。当标靶位于最短位置时，激光束与标靶交于P1点；当标靶伸出时，激光束与标靶相交于P2点。

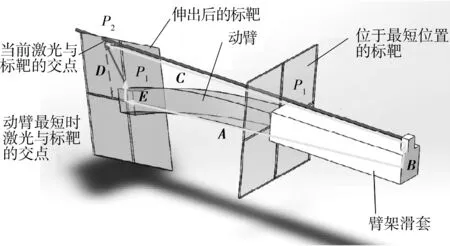
图4 伸缩臂末端位姿测量原理图

Fig.4 Schematic diagram of the telescopic arm deformation measurement

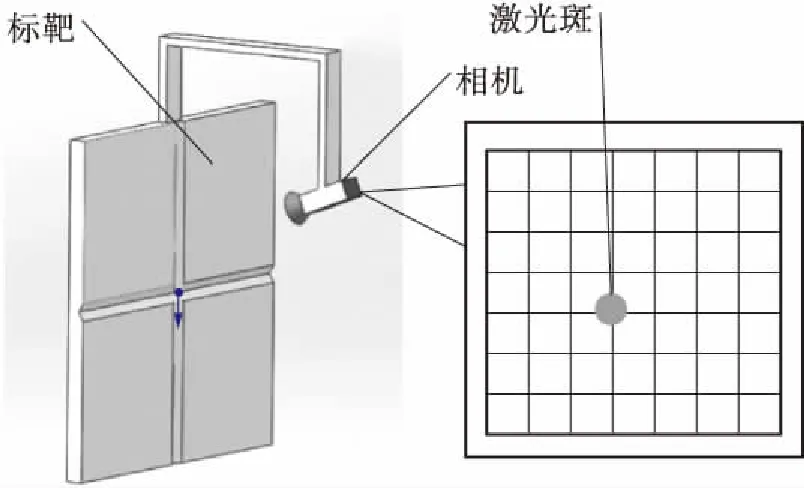
图5 基于机器视觉的标靶激光斑点位置测量示意图

Fig.5 Schematic diagram of target laser spot position measurement based on machine vision

图中：A为伸缩臂根部中心到末端中心的矢量；B为激光源与大臂根部中心的偏置矢量；C为激光发射矢量；D为P1和P2点之间的矢量；E为P1点距大臂中性面的矢量。测量装置的前端接收、激光发射装置以及总体布局如图6所示。

2.2.2 坐标系建立

大臂伸缩关节处于初始状态时，建立始端和末端坐标系。坐标系的建立方法：以标靶平面为XOZ平面，激光光线为Y轴方向，激光照射到标靶平面的光斑为原点，要求标靶平面垂直于倾角传感器的XOY平面，如图7所示。伸缩关节运动和变形时，可得到的数据信息：双轴倾角仪可以测量出标靶绕X、Y轴的旋转角度；激光测距仪可以得到标靶上某点沿Y轴的距离变化值；相机可以测量出光斑在标靶处相对于初始光斑的X、Z的偏离量，这是在当前末端坐标系下的坐标。

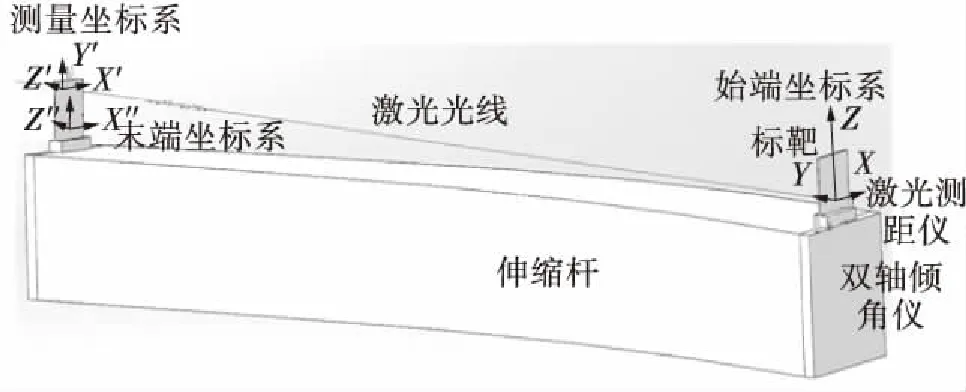
图7 坐标系分配

因此，末端与始端坐标系变换关系的建立过程如下：

(1)将始端坐标系沿Y轴(激光光线)平移激光测距仪的测量距离值E，建立一个中间坐标系，得其与始端坐标系的变换关系，如矩阵(3)所示：

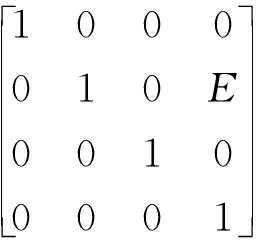
(3)

(2)将此时的坐标系按双轴倾角仪的角度绕X、Y轴旋转，得到的变换关系，如矩阵(4)所示：

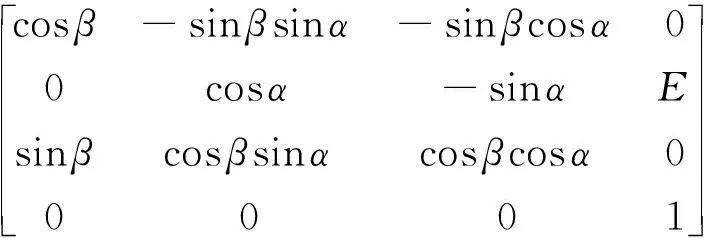
(4)

(3)因相机测量出光斑在标靶平面上相对始端原点的偏离值为M、N、L，那么此时末端坐标系的原点坐标由式(5)计算而得。

(5)

(4)末端到始端坐标系的变换关系为式(6)。

(6)

2.2.3 测量精度验证

为了验证该方法的测量精度，任意给定15组关节变量，驱动各关节至指定位置。使用全站仪测量大臂变形后的实际位置，并与测量值作比较，测试结果如图8所示。x方向平均误差为-0.007 m，y方向为0.003 m，z方向为-0.003 m，合误差为0.011 m。

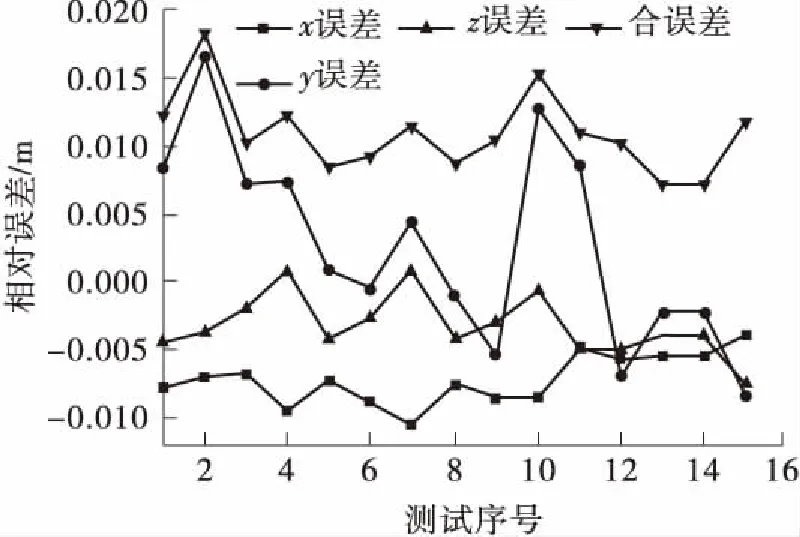
图8 柔度测量误差

2.3 机械臂参数误差补偿

基于离线标定方法，通过全站仪和角度仪对机械臂相邻两关节轴进行距离和偏转角度标定，计算出各关节参数(α，a，θ，d)的误差。根据摄动微分理论，对式(1)传递矩阵求偏导，结果如式(7)所示。

(7)

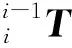
结合标定结果，得到臂架参数误差补偿模型。

(8)

3 机械臂误差补偿模型逆解算法

3.1 一次逆解

(9)

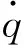
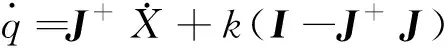
(10)

(11)

(12)

(13)

式中：k为优化速度系数；m为关节数量；qmax[i]为每个关节的最大关节变量；qmin[i]为每个关节的最小关节变量。

3.2 二次逆解

根据一次逆解得到的8个关节变量，驱动机械臂运动到该位置，然后固定前3个关节，利用柔度检测装置测量大臂的柔度误差，并构建基于测量位置的末端位姿，以补偿其柔度误差。

基于柔度检测装置得三关节末端实时位姿为

(14)

则基于三关节的末端位姿为

(15)

式中，Te表示基于基坐标系的末端位姿。

根据运动学微分运动模型，构建机械臂后5个关节的参数误差补偿运动学模型Tc，结果为

Tc=T4(I+dT4)T5(I+dT5)…T8(I+dT8)

(16)

式中：dTi(i=4，5，…，8)为关节的运动微分误差矩阵。

具体计算步骤如下：

(1)利用当前关节变量为后5个关节赋初始值qc，给定迭代收敛条件e=0.01。

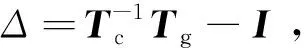
(3)将各关节变量代入对应的运动微分雅可比矩阵，建立迭代关系F=Jdq。

(4)对运动微分雅可比传递矩阵J进行SVD分解，获得其伪逆解J+，并由dq=J+F获得当前关节偏移值dq。

(5)判断是否小于给定误差‖dq‖≤e?。若满足条件，则退出迭代并输出q值；若不满足条件，则令qc=qc+dq，返回步骤(2)，重复步骤(2)-(5)，直到‖dq‖≤e为止。

4 试验验证

模拟锚杆台车的实际施工情况，选取其中15组锚杆台车期望位姿，如图9所示。其中圆圈代表选择的锚杆定位位置，其上引出的线段为锚杆在隧道中的安装位置。令φ14 m级隧道的锚杆安装面到锚杆台车大臂横摆中心的距离为7 m，其中垂直掌子面向里为坐标系x轴、y轴和z轴方向，如图9所示。

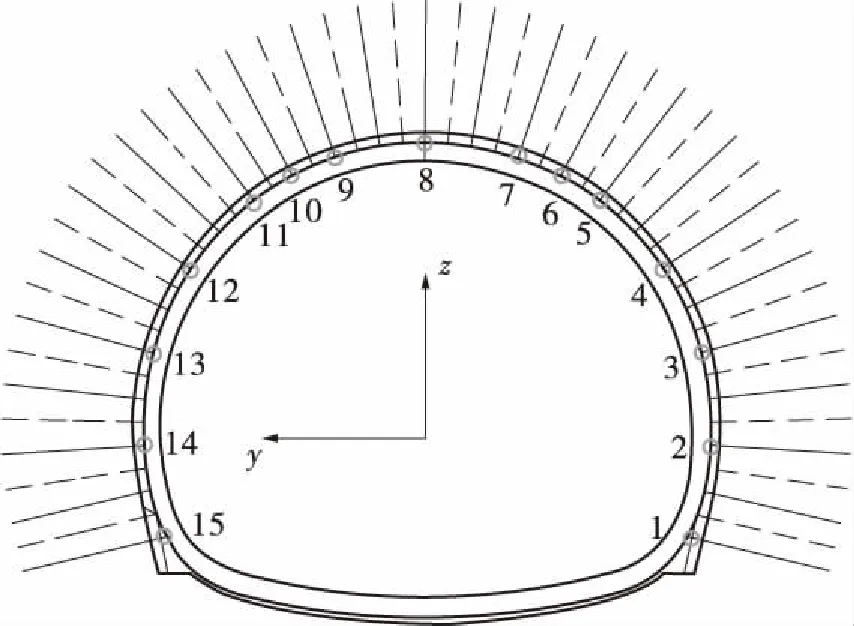
图9 隧道锚杆孔布置图

进行两次逆运动学求解，得到一组关节变量，驱动机械臂各关节至计算关节变量，采用全站仪测量末端位置，测试过程如图10所示。测量结果见表2，其中，[x，y，z]为期望坐标，[x’，y’，z’]为驱动后的末端实际坐标。

图10 现场测试

将期望坐标与实际坐标进行比较，结果如图11所示。x方向的平均误差为0.015 m，y方向为0.031 m，z方向为0.025 m，合误差为0.049 m，并且合误差基本上小于0.050m，达到工程施工要求。

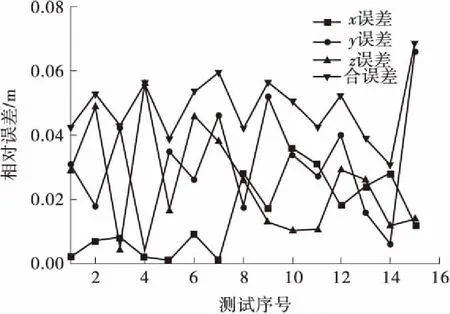
图11 末端位置误差

5 结 论

(1)锚杆台车机械臂负载和自重产生的柔度误差不容忽略，本研究提出了一种柔度误差检测方法，实时监测大臂的挠度变形，测量误差保持在0.010 m左右。

(2)通过计算测量大臂的柔度误差，结合参数误差补偿，建立了锚杆台车机械臂的运动学误差补偿模型。

(3)针对锚杆台车冗余逆解问题，提出了一种基于牛顿拉夫逊迭代算法求两次逆解的定位方法，基于梯度投影法求八自由度无误差正向运动学逆解，并根据柔度检测以及误差补偿模型对后5个关节求逆，得到给定位姿下的优化关节变量。

(4)在车间对锚杆台车进行定位试验，根据锚杆期望位姿矩阵求逆解得到优化关节变量，驱动机械臂至该位置，实测与期望位置值的合误差基本小于0.050 m，满足施工要求。