近景摄影测量像控点坐标获取的新方法
2014-08-21马洪浩
马洪浩,吴 攀,邓 晶
(1.中国石油集团工程设计有限责任公司北京分公司,北京 100085;2.西北有色地质勘查局712总队,陕西 咸阳 711200;3.中铁二十局集团第四工程有限公司,山东 青岛 266000)
0 引 言
使用近景摄影测量的方法拍摄物体时,为了将近景摄影测量网纳入到给定物方空间坐标系中,得到拍摄物体的绝对坐标,需要在拍摄范围内布设一定数量的控制点,作为数据处理时的像控点[1],一般使用人工标志作为像控点,在人工识别和测量像控点坐标时,采用黑白相间的平面人工标志。像控点的测量精度直接制约着近景摄影测量的精度[2]。
获取近景摄影测量的靶心坐标,传统方法有两种:免棱镜全站仪直接测量和测角前方交会法[3-4]。使用免棱镜全站仪测量靶心坐标,精度较低,受标靶反射状况以及天气的影响大,且免棱镜全站仪的测量距离有限,测量范围一般不超过200 m.测角前方交会的方法,在外业测量时需要在两个控制点上架站,且两控制点必须和所有像控点通视,测量工作繁琐,外业可造作性差。
1 新型标靶的设计
使用全站仪反射片测量精度高于免棱镜全站仪。因此可以考虑在近景摄影测量的标靶上安装反射片,辅助全站仪测量。
如图1所示,选择一个正方形标靶,在标靶上安装五个大小相同的正方形反射片,其中四个反射片固定在标靶的四角,反射片的两边与标靶的两边重合,反射片中心位于标靶的对角线上。一个反射片固定在标靶中心正上方,反射片的一个角点与标靶中心重合,两条边与标靶的两对角线重合。标靶以任意姿态放置时,测量四角反射片的坐标,计算靶心坐标;标靶处于竖直状态时,测量靶心正上方反射片坐标,计算靶心坐标。
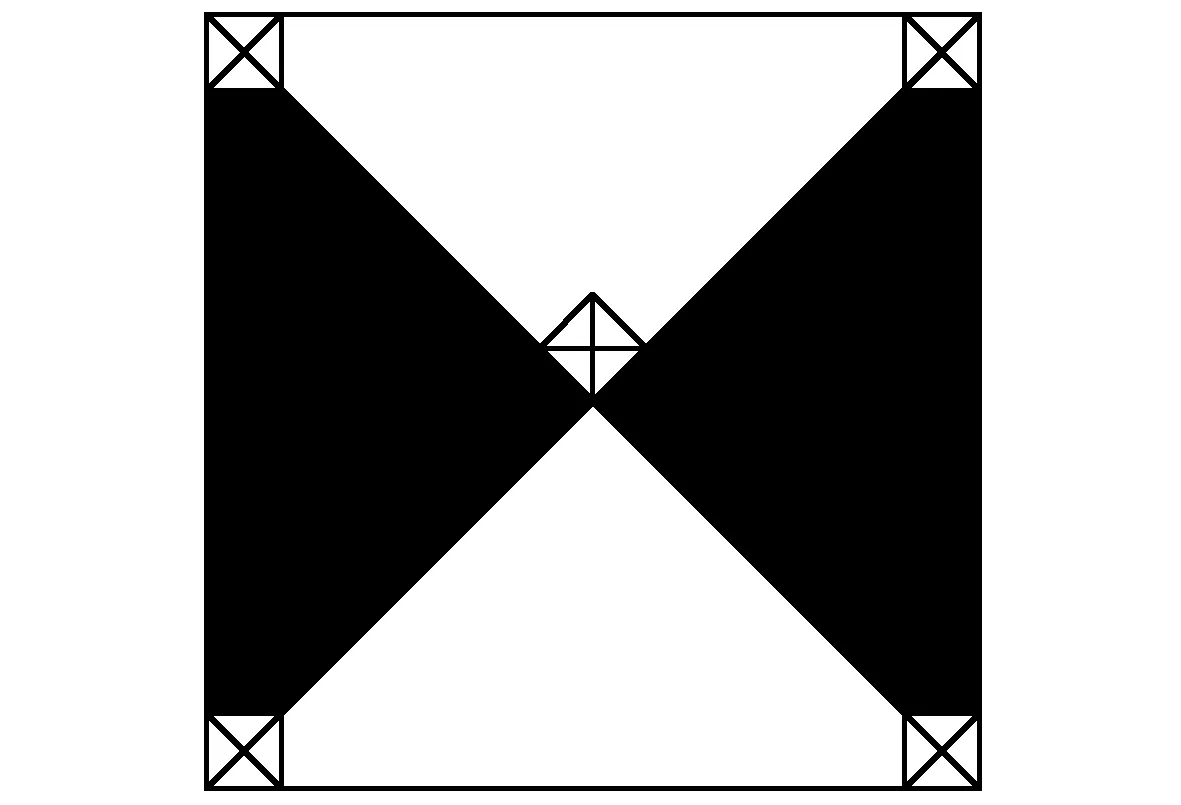
图1 新型标靶示意图
全站仪反射片在同一个标靶上,其间的距离较近,会同时出现在全站仪的视场内,全站仪在同一视场内对两个反射片的分辨角度为15′30″,当测站到两反射片之间的夹角小于15′30″时,全站仪在测量时会提示错误[5]。因此在测量标靶四角反射片坐标确定标靶中心坐标时,标靶的边长与测量距离相互制约,标靶的最小边长与测量距离的关系式为
(1)
式中:l为设计标靶的边长最小值;D为测站到棱镜间的平距;α为全站仪的最小分辨角度.
由式(1)可知,随着观测距离的增加,设计标靶的最小边长相应的增加。当标靶边长过大时,操作不便,且增加制作成本。综合考虑,设计标靶的边长l为0.6 m,D为133 m.考虑一定的观测安全系数,在观测距离小于120 m时,遮挡中间反射片,观测四角反射片,计算标靶中心坐标。当观测距离超过120 m时,全站仪无法分辨出标靶四个角点的反射片,即使分辨出,因受旁边反射片的影响,测量精度较低。这时使标靶处于竖直状态,遮挡标靶四角的反射片,直接测量标靶中心上方反射片的坐标,计算靶心坐标。
2 靶心坐标的计算方法及精度分析
2.1 近距离测量靶心坐标计算方法及精度分析
如图1所示,以标靶左上角为起点,按顺时针方向反射片的编号分别为1、2、3、4.标靶中心坐标为(x,y,z)。反射片中心的坐标为:(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)、(x4,y4,z4).
观测距离较近时(D<120 m),测量四角反射片坐标,计算靶心坐标。标靶中心与任一对角线上的两个反射片的中心位于同一条空间线段上,且平分该空间直线。取任意两个对角点反射片中心的坐标,求平均值即可得到标靶中心坐标。
由于测量误差的存在,需要对测量后的反射片坐标值进行平差处理,以得到高精度的靶心坐标。给出三种靶心坐标的计算方法,分析对比三种方法的求解精度,选取最优算法。
2.1.1 平均值法
确定标靶中心坐标值,必要观测数据6个,文中有12个观测数据,可计算出两组靶心坐标值,取两组坐标的平均值为标靶中心坐标的最终值,靶心坐标的表达式为
(2)
2.1.2 空间正方形平差法
四个反射片的中心构成一个空间正方形,靶心位于这个空间正方形的中心。由于存在测量误差,四个反射片所组成的空间四边形不是一个严格意义上的正方形。因此可以先进行条件平差,提高观测正方形的内符合精度,再计算空间正方形的中心坐标。存在6个多余观测条件,可列出6个条件方程。
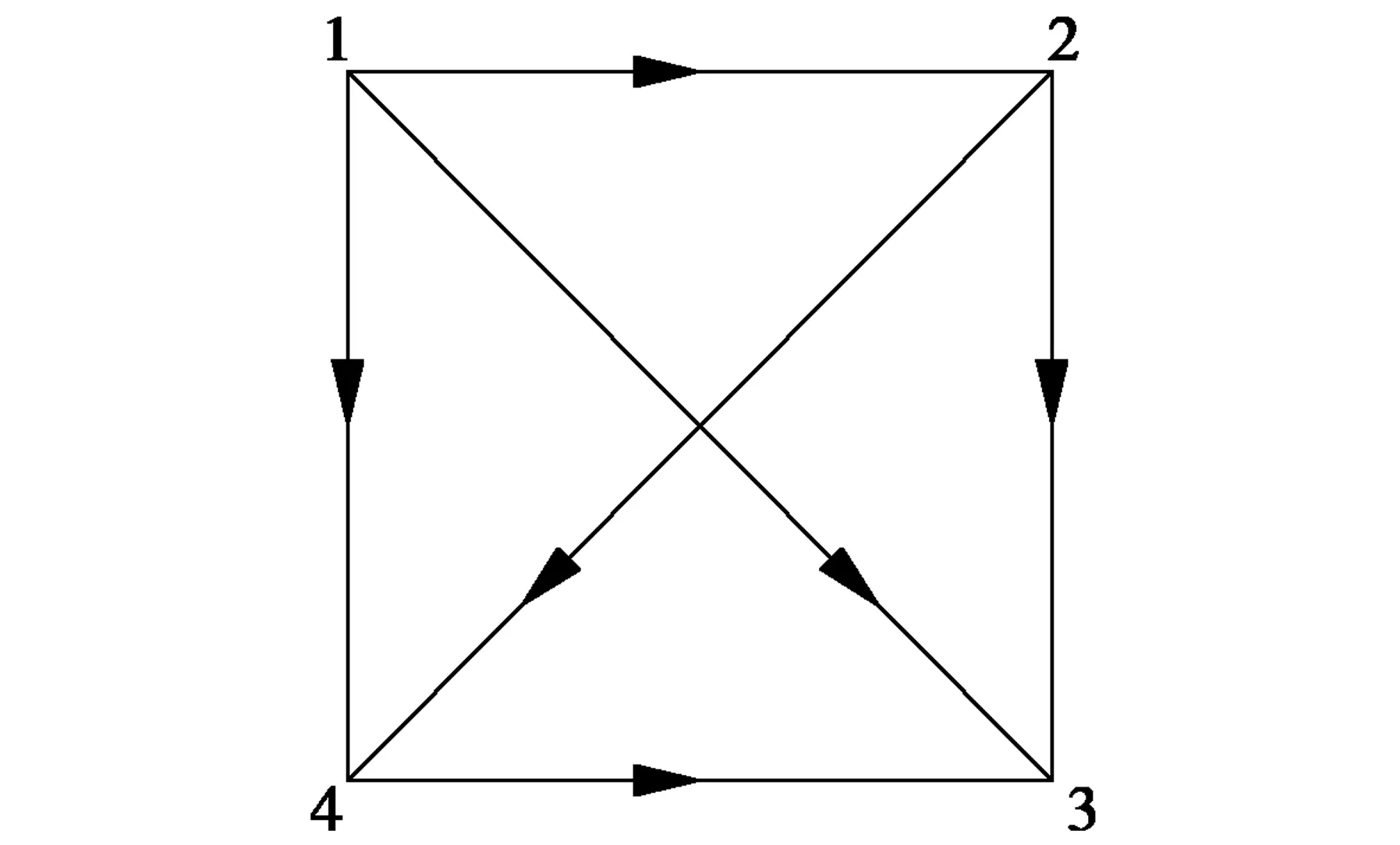
图2 空间正方形条件平差示意图
如图2所示,若确定一个边长已知的空间正方形,充要条件是:对边平行且相等, 即12=34;对角线垂直,即24^13;相邻两边垂直,即12^14;其中一条边的长度为已知值d,令12=d.条件方程如下:
(3)
(4)
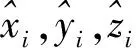
平差后得出反射片中心坐标的改正数,对观测坐标进行改正,得到平差后的坐标,再使用式(2)计算靶心坐标。
2.1.3 球心拟合法
标靶四个角的反射片中心到标靶中心的距离相等,四个反射片的中心在以靶心为球心半径已知的球面上。已知球面上三个点和球的半径可以确定一个空间球体。观测到球面上四个点的坐标,且球的半径已知,存在三个多余观测量,采用最小二乘法拟合出球心坐标,球心坐标算式为
(x+Δx-xi)2+(y+Δy-yi)2+
(z+Δz-zi)2=r2,
(5)
式中:x,y,z为球心坐标初值; Δx,Δy,Δz为球心坐标改正数;r为球的半径。
将上式展开,球心坐标的改正数较小,略去二次项:
(x-xi)Δx+(y-yi)Δy+(z-zi)Δz
(6)
四组三维坐标观测值,列出四个方程,用最小二乘法求出球心坐标的改正数,对球心坐标初值进行改正。将改正后的坐标值再代入式(6),作为下次计算的初值,反复迭代,直到改正数小于规定的数值后,停止迭代。
进行数值实验,对比三种方法的平差效果。取标靶的边长0.6 m,全站仪反射片的边长2 cm.给出标靶在15种不同姿态下四角反射片中心的坐标真值,计算出靶心坐标的真值。对15组坐标值添加随机噪声。噪声符合标准正态分布,标准差分别为5 mm、10 mm、15 mm和20 mm.采用上述三种平差方法,对添加随机噪声后的反射片坐标进行处理,计算靶心坐标,与标靶中心坐标的真值对比,求出三种平差方法计算靶心坐标的中误差,如表1所示。

表1 标靶中心坐标中误差
由表1可知,采用上述的三种平差方法,都不同程度的提高了靶心坐标的计算精度。球心拟合法的精度低于平均值法和空间正方形平差法。分析原因,由于球心拟合法的多余观测条件少于前两种方法,且四个反射片的中心位于同一平面上,球心拟合的几何条件较差。
空间正方形平差法,改正后的反射片坐标所组成的图形更接近正方形,提高了四个坐标间的内符合精度。但是对于提高正方形中心坐标精度的效果并不明显,与平均值法相比,两者在亚毫米级上精度是相同的,对于提高像控点坐标精度的意义不大。
综合比较,平均值法求解标靶中心坐标精度较高,计算简单。且对于标靶的形状没有特殊要求,只需要保证对角线上的两个反射片到标靶中心的距离相等。确定平均值法为计算靶心坐标的最优方法。
2.2 远距离测量靶心坐标计算方法及精度分析
观测平距超过120 m时,遮挡四角反射片,只观测标靶中心正上方反射片的坐标。当标靶处于竖直状态时,将反射片坐标在竖直方向上减去反射片对角线长度的一半,即可得到标靶中心坐标。若标靶发生倾斜时,使用这种方法计算靶心坐标,会造成一定误差。
选择边长为2 cm的反射片,取标靶的倾角分别为:5°、10°、15°、20°、25°、30°.标靶不同程度的倾斜造成的靶心坐标计算误差如表2所示。当标靶的倾斜角度较小时,由于反射片的边长很小,倾斜引起的误差不大。使用这种方法测量像控点坐标时,若要求的测量精度很高,观测时应安装水准气泡,使标靶处于竖直状态。当近景摄影测量要求的精度降低时,可以根据近景摄影测量对像控点要求精度的高低,允许标靶有所倾斜,提高外业测量的可操作性。

表2 标靶不同程度的倾斜引起的靶心坐标计算误差
3 新型标靶与传统测量方法对比
文中设计的新型标靶通过测量标靶上全站仪反射片的坐标来间接获取靶心坐标,与免棱镜全站仪测量的方法相比,两者测量坐标的原理都是极坐标法。新型标靶使用了反射片,改善了全站仪测距脉冲的反射条件,提高了测量精度,且不受观测距离的影响。
采用新型标靶获取点坐标与测角前方交会的方法相比,两者的测量原理不同。它们获取待测点高程坐标都采用三角高程法,因此高程测量误差相似,对比点位的测量精度时,只需分析两者的平面测量精度。
设有两个控制点A、B,用极坐标法测量待测点坐标时,在A点架设全站仪,后视B点,测量待测点坐标。用测角前方交会的方法测量待测点坐标时,分别在A、B两点架设全站仪,测角交会待测点坐标。根据两种方法的坐标计算式以及中误差传播定律,得极坐标法测量点平面坐标的中误差m1为
(7)
测角前方交会测量点平面坐标的中误差[6]m2为
(8)
式中:ms为测边误差;mα为测角误差;D1为控制点A到待测点的平距;D2为 控制点B到待测点的平距;γ为 待测点与两已知控制点间的夹角。
当全站仪的技术参数和观测的测回数确定后,测角中误差为一定值,极坐标法的平面坐标测量误测角中误差为一定值,极坐标法的平面坐标测量误差只受测量距离的影响。测角前方交会法,误差除受两已知控制点到待测点间距离影响外,还受待测点与两已知控制点间的夹角影响。
选用常用的2″全站仪,测距精度为1 mm+1 ppm,进行一测回观测。假设控制点A、B到待测点的距离相等,绘制极坐标法和测角前方交会法平面坐标测量误差随观测距离变化的曲线图,测角前方交会法令γ分别为90°、60°、30°,如图3所示。
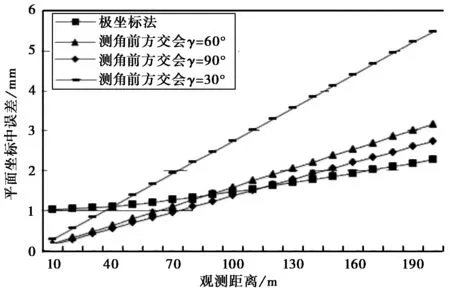
图3 待测点平面坐标误差曲线图
由图3可知,两种方法的坐标测量误差都随着观测距离的增加而增大。测角前方交会的方法在测距较短时精度高于极坐标法,随着观测距离的增加其测量精度的下降速度大于极坐标法。且其误差值会随着待定点与已知点间夹角γ的减小而增大。使用测角前方交会确定点坐标时,当观测距离超过某一值时D,其观测量误差就会超过极坐标法,夹角γ越小,这一观测距离值D越小。
因此,测角前方交会法适应于近距离测量,特别是室内的像控点坐标测量,观测距离近,测量精度高,方便在两已知点架站。极坐标法适应于远距离测量,尤其是在野外测量像控点坐标,它的点位测量精度不受控制点和待测点之间几何关系的影响,在点位选取时更具灵活性,观测过程中只需在一个已知点架站,外业工作量小。
目前,许多学者将近景摄影测量技术应用于采煤塌陷区、边坡、滑坡的监测[7-10],观测距离长,且均在野外作业,适用文中设计的新型标靶。
4 结束语
本文设计的新型标靶适用于不同的观测距离。观测距离近时(D<120 m),标靶可以按任意姿态放置,遮挡中间的反射片,测量四角的反射片坐标,采用平均值法计算标靶中心坐标。观测距离远时(D>120 m),可根据近景摄影测量要求的测量精度,使标靶处于竖直状态或允许产生一定小角度的倾斜,遮挡四角的反射片,测量中间反射片坐标,在竖直方向上减去反射片对角线长度的一半得标靶中心坐标。
采用本文设计新型标靶,与免棱镜全站仪相比,提高了测量精度。与测角前方交会法相比,提高了远距离观测时像控点的测量精度,且不受控制点与待测像控点间位置关系的限制,外业可操作性更强,适用于室外小区域的变形监测。
[1] 冯文灏.近景摄影测量的控制 [J]. 武汉测绘科技大学学报,2000,25(5):453-458.
[2] 冯文灏.近景摄影测量[M].武汉:武汉大学出版社,2002:86-87.
[3] 刘昌华,王成龙,李 峰,等.数字近景摄影测量在山地矿区变形监测中的应用[J].测绘科学,2009,34(6):197-199.
[4] 程光亮,王宝山.空间前方交会法测定像控点的精度分析[J]. 测绘与空间地理信息,2008,31(6):40-42.
[5] 徐 强.TCA2003测量机器人在沉陷变形监测中的应用研究[D].徐州:中国矿业大学,2011.
[6] 田林亚,周照明,滕 松. 四种常用坐标测量方法的精度对比[J]. 测绘工程,2009,18(6):37-39.
[7] 盛业华,闻志刚,宋金铃.矿山地表塌陷区的数字近景摄影测量监测技术 [J].中国矿业大学学报,2003,32(4):411-415.
[8] 杨化超,邓喀中,张书毕,等.数字近景摄影测量技术在矿山地表沉陷监测中的应用研究[J]. 中国图象图形学报,2008,13(3):519-524.
[9] 项 鑫,王艳利. 近景摄影测量在边坡变形监测中的应用 [J].中国煤炭地质,2010,22(6):66-69.
[10] 王秀美,贺跃光,曾卓乔.数字化近景摄影测量系统在滑坡监测中的应用[J].测绘通报,2002(2):28-30.
