基于CEEMDAN的爆破地震波信号时频分析

孙苗 吴立† 袁青 周玉纯 马晨阳 汪煜烽

(1.中国地质大学(武汉)岩土钻掘与防护教育部工程研究中心∥工程学院，湖北 武汉 430074；2.中交第二航务工程局有限公司博士后科研工作站，湖北 武汉 430040)

爆破地震信号表现为瞬时、突变和震荡特征，属于典型的非平稳信号[1- 2]。时频分析已成为处理这类信号的重要手段[3- 4]。常用的时频分析方法有短时傅里叶变换、Wigner-Ville分布、连续小波变换等[5- 6]。这些方法的理论依据都是傅里叶变换，从而不可避免地会出现使用傅里叶变换分析非平稳信号所带来的缺陷，如出现虚假频率和多余信号分量等[7- 8]。针对这一问题，Huang等[9]于1998年提出的经验模态分解(EMD)从根本上突破了傅里叶变换理论的限制，首次建立了一种基于瞬时频率的信号分析方法[10- 11]。它不受傅里叶分析的局限，依据数据本身的时间尺度特征来进行模态分解，分解的过程保留了数据本身的特性。但也存在一些问题，如模态混淆[12]现象，即同一个固有模态函数中出现了不同频率的信号，或者同一频率的信号被分解到多个不同的固有模态函数当中。

因此本研究在对EMD固有的模态混淆问题进行分析的同时，对其改进算法集合经验模态分解(EEMD)也进行了深入探讨，发现EEMD通过添加白噪声抑制模态混淆，对模态混淆有一定的抑制作用，但是效果不太明显。由于人为引入的白噪声无法证明可以完全抵消[13]，为了更好地抑制模态混淆，必须对EEMD进行进一步改进。自适应补充集合经验模态分解(CEEMDAN)是在每个阶段添加有限次的自适应白噪声，能实现在较少的平均次数下，重构误差几乎为零。该算法在程序上实现了添加自适应白噪声，解决了EEMD添加随机噪声的不足，可以很好地消除人为添加噪声对原始信号完备性的影响，既抑制了模态混淆又避免了原始信号失真。本研究通过比较EMD、EEMD、CEEMDAN对仿真信号的分解结果；计算EMD、EEMD、CEEMDAN得到的固有模态函数(IMF)的排列熵值；对EMD、EEMD、CEEMDAN的分解结果进行Hilbert变换，并比较三者的时频谱分辨率；为验证CEEMDAN抑制模态混淆的有效性，进一步针对CEEMDAN分解结果进行Hilbert变换，得到时频谱，该时频谱在时域和频域都具有较高的分辨率，对爆破振动危害控制具有重要的意义。

1 希尔伯特-黄变换和排列熵

1.1 希尔伯特-黄变换

希尔伯特-黄变换是通常意义上说的HHT，是目前应用最广泛的时频分析方法之一。其由两部分组成，第1部分是经验模态分解，第2部分是希尔伯特变换。

1.1.1 经验模态分解

经验模态分解(EMD)是根据信号本身的时间尺度特性，将信号分解为含有不同时间尺度且满足一定条件的一组IMF，算法具体步骤见文献[14]。

集合经验模态分解[15](EEMD)是在EMD的基础上，加入多组白噪声信号，用于抑制经验模态分解过程中出现的模态混淆现象。

自适应补充集合经验模态分解[16](CEEMDAN)是在每个阶段添加有限次的自适应白噪声，能实现在较少的平均次数下，重构误差几乎为零。具体步骤如下：

(1)在原始信号S(t)中添加自适应性白噪声Bi(t)，其中i表示添加噪声次数，一般取10～50，本研究取i=50。则第i次的信号可表示为S(t)=S(t)+αiBi(t)(i=1，2，…，50)，其中αi为第i次添加白噪声的标准差。CEEMDAN的一阶IMF分量为

(1)

余项R1(t)=S(t)-IMF1。

(2)构造新的待分解信号S(t)，S(t)=R1(t)+αiBi(t)，进行50次分解。得到CEEMDAN的二阶IMF分量：

(2)

余项R2(t)=S(t)-IMF2。

(3)重复式(1)和(2)，直到程序终止，共产生了k个IMF，则最后的余项为

(3)

1.1.2 希尔伯特变换

关于希尔伯特变换详细见文献[17]，这里主要介绍希尔伯特时频谱，简称时频谱。时频谱是幅度在时间频率平面上的分布，采用颜色编码图的形式表示，时频谱的表达为

(4)

式中：Re为实部；i为IMF的个数，i=1，2，…，n；ai(t)为幅值函数；ω(t)为频率函数。

1.2 排列熵

排列熵(PE)是一种检测时间序列随机性和动力学突变的方法，具体步骤见文献[18]。根据文献[19- 20]，当时间序列的PE大于0.6时，其被认为是异常的非平稳随机信号，否则近似认为是平稳信号。因此计算每一个IMF的PE，可以判断该IMF的随机性，对于模态混淆轻微甚至没有模态混淆的IMF，其PE值一定是小于0.6的，因此排列熵检测可以对模态混淆现象起到一定的评估作用。

2 仿真信号希尔伯特-黄变换

2.1 仿真信号的建立

仿真信号构建如图1所示。其中x1是功率为0.4的高斯白噪声；x2是频率为100 Hz的稳态正弦信号。仿真信号S=x1+x2，采样点数N=512，时间t=1/N：1/N：1。

图1 仿真信号波形图

2.2 仿真信号的模态分解

仿真信号经不同方法的分解结果如图2所示，图中R的定义同式(3)。图2(a)为EMD结果，可发现高频模态混淆很严重，如IMF1，低频相对稳定；图2(b)是EEMD结果，高频信号模态混淆较EMD有所缓解，低频相对稳定；图2(c)为CEEMDAN结果，分解结果从高频向低频依次排列，模态混淆得到了有效的抑制。

(a)EMD

(b)EEMD

(c)CEEMDAN

Fig.2 Decomposition results of simulation signals with different methods

2.3 仿真信号的固有模态函数排列熵值

根据排列熵的定义，选取m=6，σ=1计算仿真信号的排列熵[18- 20]，x1的PE值为0.967 1，x2的PE值为0.127 5。根据排列熵的物理意义可发现：白噪声信号序列随机，PE值大，发生突变的概率大；正弦信号序列规则，PE值小，信号稳定。

表1的运算结果和图2的分解结果相对应，EMD和EEMD高频模态混淆严重，因此计算出高频分量熵值大于0.6，低频相对稳定，熵值也相对减小；EEMD中低频分量稳定，相应的熵值也小于0.6；CEEMDAN每个分量的排列熵均小于0.6，侧面说明了CEEMDAN得到的分量均具有稳定性，即CEEMDAN对模态混淆具有一定的抑制作用，且该作用明显强于EMD和EEMD。

表1 各分量排列熵值大小

2.4 仿真信号的希尔伯特变换

将仿真信号经EMD、EEMD、CEEMDAN得到的IMF分量，经过Hilbert变换可以得出时频谱，如图3所示。

根据图3可发现，时频谱图结果和IMF分解结果对应。图3(a)为采用EMD时得到的时频谱图，可发现在噪声的干扰下出现了大于100 Hz的虚假分量，且虚假分量难以识别，模态混淆严重，高频分量时域和频域分辨率不高；图3(b)为采用EEMD时得到的时频谱图，可发现高频分量模态混淆有所缓解，但高频分量时域和频域分辨率依旧不高，低频分量稳定性高于EMD分解结果，时域和频域分辨率较EMD有所提高；图3(c)为采用CEEMDAN时得到的时频谱图，可发现模态混淆现象得到了有效的抑制，时频谱图在时域和频域的分辨率都很高，通过图3(c)右侧的颜色编码棒(点颜色越深，能量越大)可发现信号时间-频率-能量之间的关联，例如在0～200这一采样段内，频率为10、20以及30 Hz的分量携带了大量的能量。

(a)EMD

(b)EEMD

(c)CEEMDAN

Fig.3 Time-frequency spectrum diagrams with different decomposition methods

根据第2节的分析，可发现CEEMDAN不仅可以有效抑制模态混淆，且其分解得到的IMF通过Hilbert变换得到的时频谱图在时域和频域分辨率都很高，有助于更好地识别爆破振动特征，控制爆破振动的危害。

3 基于CEEMDAN的爆破振动信号时频分析

3.1 工程概况

以长江上游九龙坡至朝天门河段砖灶子滩段炸礁工程为研究对象，炸礁区处于李家沱大桥主跨下。砖灶子礁石长约400 m，宽约150 m，为孤礁石，坐落于河心，将枯水河槽分为左右两槽，炸礁区平面如图4所示。

图4 砖灶子炸礁区平面图

3.2 信号获取

采用TC- 4850型爆破测振仪对李家沱大桥进行监测，测点布置见图4，观察实测爆破振动数据发现：水下钻孔爆破的3个方向分量振动信号中水平径向峰值振动速度最大，水平切向次之，而垂直方向振动速度最小。仅对测点A的水平径向峰值振速进行基于CEEMDAN的爆破振动信号时频分析研究，实测地震波径向振动速度波形图见图5，经CEEMDAN分解后得到图6。

3.3 CEEMDAN在实测爆破振动地震波信号中的应用

实测爆破地震波信号采样频率为4 000 Hz，根据奈奎斯特采样定理，实测爆破地震波信号的奈奎斯特频率值为2 000 Hz，共包括9 601个采样点。由图6可知，图5实测地震波信号经CEEMDAN被分解成7个IMF和一个余项R(定义同式(3))。观察图6，可发现CEEMDAN分解出的每一个IMF都具有清晰的物理意义，分量IMF1频率最高，所占能量小；IMF2到IMF5频率逐渐降低，同时IMF2-IMF5包含了振动信号的大部分能量，为优势频带，水下钻孔爆破危害效应主要由这些分量构成，是研究的重点频带；IMF6-IMF7为低频分量，残余分量R为信号本身微弱的趋势或者仪器的漂零。CEEMDAN结果可清晰展示实测爆破振动数据内部蕴含的信号频率信息，清晰地区分开了高频、中频和低频。由此结果可见，噪声信号引起的模态混淆得到了很好的抑制。

图5 实测地震波径向振动速度波形

Fig.5 Measured radial vibration velocity waveform of seismic wave

图6 基于CEEMDAN的实测爆破振动信号分解结果

Fig.6 Decomposition results of blasting vibration signal based on CEEMDAN

进一步的分析是对CEEMDAN得到的IMF进行Hilbert变换，得到实测地震波信号的时频谱，结果见图7。

由图7可以发现，基于CEEMDAN得到的时频谱图在时域和频域都拥有很高的分辨率；观察图7(b)可发现，水下钻孔爆破地震波能量主要集中在100 Hz以下的低频段，主要在0～50 Hz，特别是 0～30 Hz。结合图7(b)右侧的颜色编码棒可发现在0～30 Hz，2 000～6 000这一采样时间段是本次爆破能量的聚集段，应该重点关注。

考虑到本工程爆破区域主要的被保护对象为李家沱大桥，爆破地震波是否会引起其共振是本次爆破主要的安全问题[21]。根据瑞士实验室EMPA对桥梁跨径在11.0～118.8 m之间的简支梁及连续梁大跨跨中进行的振动位移测量实验，发现满足该跨径区间桥梁的基频在1.23～14.00 Hz之间[22]。李家沱大桥跨径组合为：53+169+444+169+53 m(省略引桥长度)，因此其基频在1.23～14.00 Hz的范围内。鉴于此本工程爆破地震波是否会引起李家沱大桥共振的问题不容忽视，针对此现象建议施工采用降低单段药量法、微差起爆、优化装药结构等增频方法，或设置减震孔、减震沟来削弱爆破地震波强度。

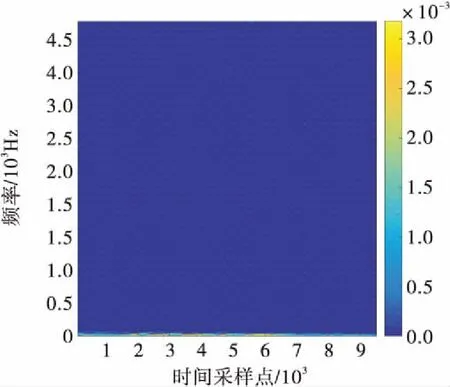
(a)基于CEEMDAN的时频谱图

(b)0～1 000 Hz细节图

综上可发现，基于CEEMDAN的爆破地震波信号时频分析方法，不仅有助于抑制含噪监测信号引起传统经验模态分解结果的模态混淆现象，同时CEEMDAN得到的IMF经过Hilbert变换得到的时频谱在时域和频域上都具有较高的分辨率，有助于爆破振动特征的识别和爆破振动危害控制。

4 结论

(1)CEEMDAN在EMD分解的每个阶段添加有限次的自适应白噪声，即使在集成次数较少的情况下，其重构误差几乎为零，重构后的信号与原信号几乎完全相同，在保证重构信号完备性的同时，能够在一定程度上抑制模态混淆，具有优越性。

(2)基于CEEMDAN的爆破地震波信号时频分析方法，不仅有助于抑制含噪监测信号引起传统经验模态分解结果的模态混淆现象，同时CEEMDAN得到的IMF经过Hilbert变换得到的时频谱在时域和频域上都具有较高的分辨率，有助于爆破振动特征的识别和爆破振动危害控制。

(3)基于实测爆破地震波信号时频谱图可发现，本工程爆破振动信号能量主要集中在0～50 Hz的低频区域内，特别是0～30 Hz的范围内。李家沱大桥基频为1.23～14.00 Hz，处于爆破振动能量集中区的范围内。因此本工程爆破施工是否会引起李家沱大桥共振的问题不容忽视，爆破施工时应密切监控桥梁安全。