基于改进的快速趋近律的四旋翼姿态控制

张 文,孙瑞胜

(1.南京理工大学泰州科技学院，泰州 225300；2.南京理工大学 能源与动力学院，南京 210094)

0 引 言

近年来，四旋翼飞行器因结构简单、操作灵活，受到越来越多的学者和科学家的关注。通过深入开发研究，四旋翼飞行器在很多方面都得到了广泛的应用，比如在航拍摄影、无人侦察、森林防火、城市巡逻以及在各种恶劣环境下的灾情监测等领域。

四旋翼飞行器的结构简单源于其机械构造。它的四个旋翼分别由4个电机带动。如果调整4个电机，让它们的转速发生变化，就可以改变飞行器的姿态，从而实现对姿态的控制。4个电机的转速之间存在差异，电机所对应的旋翼升力就会产生变化，从而飞行器的姿态也发生相应的改变。

在运动期间，飞行器的姿态可以通过6个自由度来描述：围绕X，Y以及Z轴的俯仰、滚转、偏航运动；上下的垂直运动，以及前后、左右的两个平移运动。这6个自由度通过4个控制量来进行控制。自由度的数目大于控制量的数目，符合欠驱动系统的特征，因此四旋翼飞行器属于欠驱动系统。此系统不但非线性比较严重、耦合性比较强，而且还容易被外界因素所干扰，具有很强的不确定性。但是这些问题都可以通过采用控制器得到改善，改善的结果取决于控制器所采用的控制算法，即控制算法直接决定了控制质量。因此，许多学者都希望能够研究出一个好的控制算法来实现对飞行器的快速稳定控制。其中，比较突出的有K Erbatur[1]等，他们设计的是一种高增益的滑模控制器，此控制器可以模糊、自动地调整边界层的厚度。针对滑模控制器存在的抖振问题，高为炳[2]设计了一种变结构控制系统。针对有较强干扰存在的伺服系统，A Kawamura[3]等将观测器与传统的滑模控制方法相结合，设计了一种新型的观测器。对于没有确定数学模型以及动态性能不确定的机械系统，G Bartolini[4-5]等设计了切换函数的二阶导数，有效地消除了抖振现象，同时进一步将这种方法应用到了多输入系统中。Zhuang K Y等[6]则是通过调整增益来降低抖振现象，具体是对于系统的不确定项利用模糊控制在线估计，实现增益的自适应调整。目前，对四旋翼飞行器主要采取的智能控制方法有自适应控制、滑模控制、模糊控制等。

本文针对传统趋近律，对控制器做了一定的改进，并进行了仿真分析，仿真结果表明所设计的控制器是有效的。

1 数学模型[6]

在各种坐标系描述方法中，我们通常采用机体坐标系或者惯性坐标系来描述四旋翼飞行器。飞行器在惯性空间的位置用ξ=[x,y,z]T来表示，而飞行器的姿态滚转角、俯仰角及偏航角用η=[φ,θ,ψ]T表示。可以用矩阵R实现的转换。

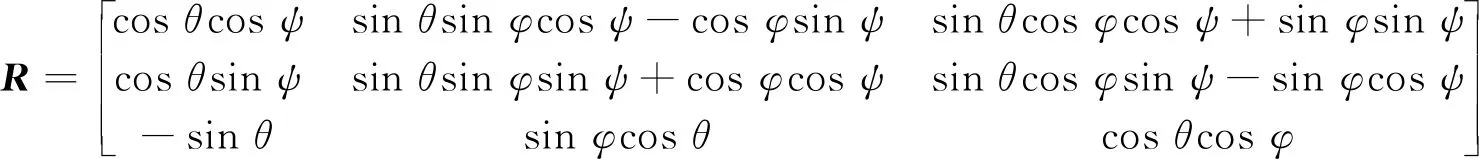
(1)

忽略摩擦阻力、大气对螺旋桨的干扰以及陀螺效应等影响因素，对飞行器进行受力分析，推导出飞行器的动力学模型：

(2)

式中：Ki(i=1,2,…,6)为阻力系数；Ij(j=1,2,3)为转动惯量；m为飞行器的质量;g为重力加速度;l为飞行器的半径。

U1,U2,U3,U4分别为垂直、滚转、俯仰以及偏航的输入控制量。

(3)

式中：Fi(i=1,2,3,4)为对应的4个旋翼的升力。

2 全驱动子系统控制器的设计

根据动力学理论，飞行器有6个自由度，4个控制量，可以将模型进行分解，分为全驱动和欠驱动两个子系统，这两部分的控制器应单独进行设计。

将高度和偏航角划分为全驱动子系统部分，设计控制器。

(4)

定义高度的跟踪误差e=zd-z，其中，飞行器的高度用z表示，即飞行器在z轴方向的位移，飞行器高度的期望值用zd表示。

2.1 传统的指数趋近律[7]

传统的指数趋近律如下：

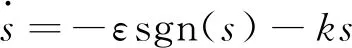
(5)

式中：k,ε为大于0的常数。

2.2 改进的快速趋近律

为了更好发挥趋近律的作用，加快系统到达滑模面，本文对指数趋近律作了如下改进：

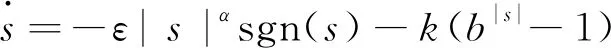
(6)

式中：α>0,b>1,ε>0,k>0。

此系统可以在某个时间收敛到平衡点。

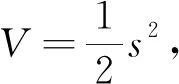
(7)

仅当s=0时，式(7)等于0，系统满足Lyapunov稳定条件，是渐进稳定的，可以收敛到平衡点。

当系统的状态在远离滑模面时，式(7)右边的第二项起主要作用，此时可加快系统远离滑模面的速度。当系统的状态接近滑模面时，第一项起主要作用，同样可以使得系统以较快的速度趋近滑模面。这样使得系统在远离滑模面以及接近滑模面时都能以较快的速度趋近滑模面，达到快速趋近的目的。

定义系统的滑模面：

采用指数趋近律式(6)，设计控制律：

(8)

式中：zd为飞行器高度的期望值，e=z-zd，k3>0。

(9)

满足Lyapunov稳定性定理。同理，可得到偏航角的控制器：

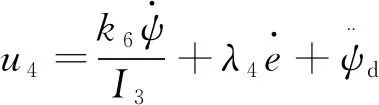
(10)

式中:k6>0，λ4>0。

3 欠驱动子系统的滑模控制器设计

欠驱动子系统的描述有多种形式，下面采用了其中一种标准形式：

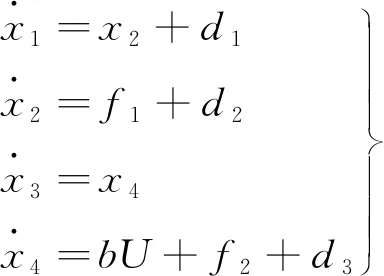
(11)

式中：d1，d2，d3为扰动项；U为控制量。

四旋翼飞行器欠驱动子系统模型：

(12)

式中：Ij(j=1,2)为转动惯量；m为飞行器的质量；l为飞行器的半径；Ui(i=1,2,3)为控制变量。

将式(1)改写：

(13)

与标准形式比较，可得d1=d2=d3=0,

取误差方程：

(14)

定义系统的滑模面：

s=c1e1+c2e2+c3e3+e4

(15)

式中：ci>0,i=1,2,3。

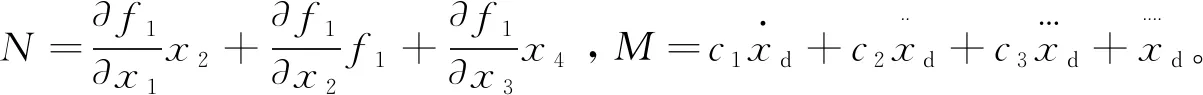
采用指数趋近律：

设计控制律：

根据Lyapunov稳定定理，系统稳定。

4 仿 真

本文运用MATLAB对飞行器进行了仿真研究。控制目标从地面的(2,2,0)到期望的目标位置(0,0,5)，偏航角的期望值为50°，俯仰角和滚转角能够稳定地保持在0。飞行器的参数设置：m=2 kg，g=9.81 m/s2，I1=I2=1.25 kg·m2，I3=2.5 kg·m2。采用传统滑模控制器以及本文设计的滑模控制器对飞行器进行仿真分析，得到系统的响应曲线，其中图1为高度响应曲线，飞行器的3个姿态响应曲线分别为图2、图3以及图4。

图1 高度响应曲线

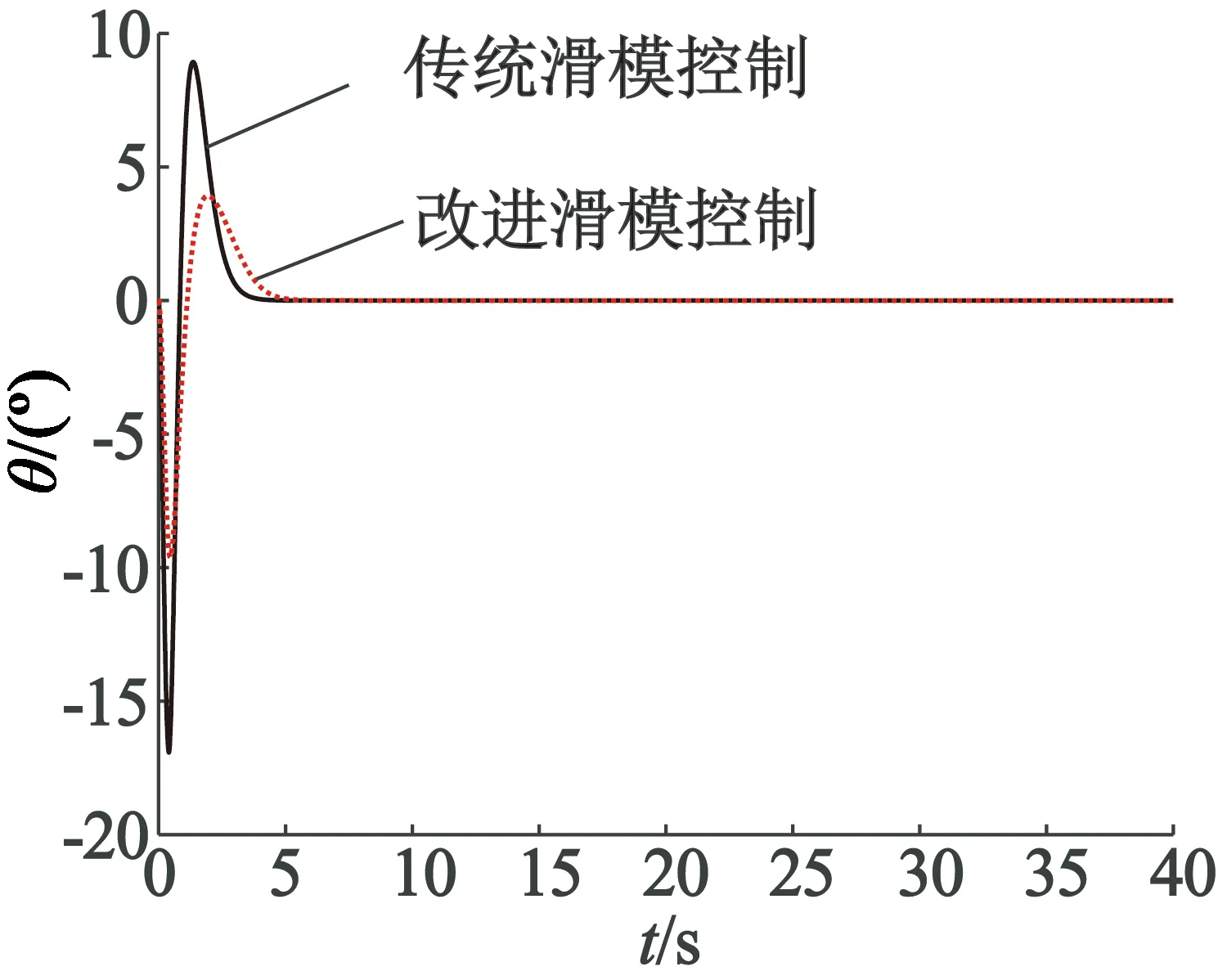
图2 俯仰角响应曲线

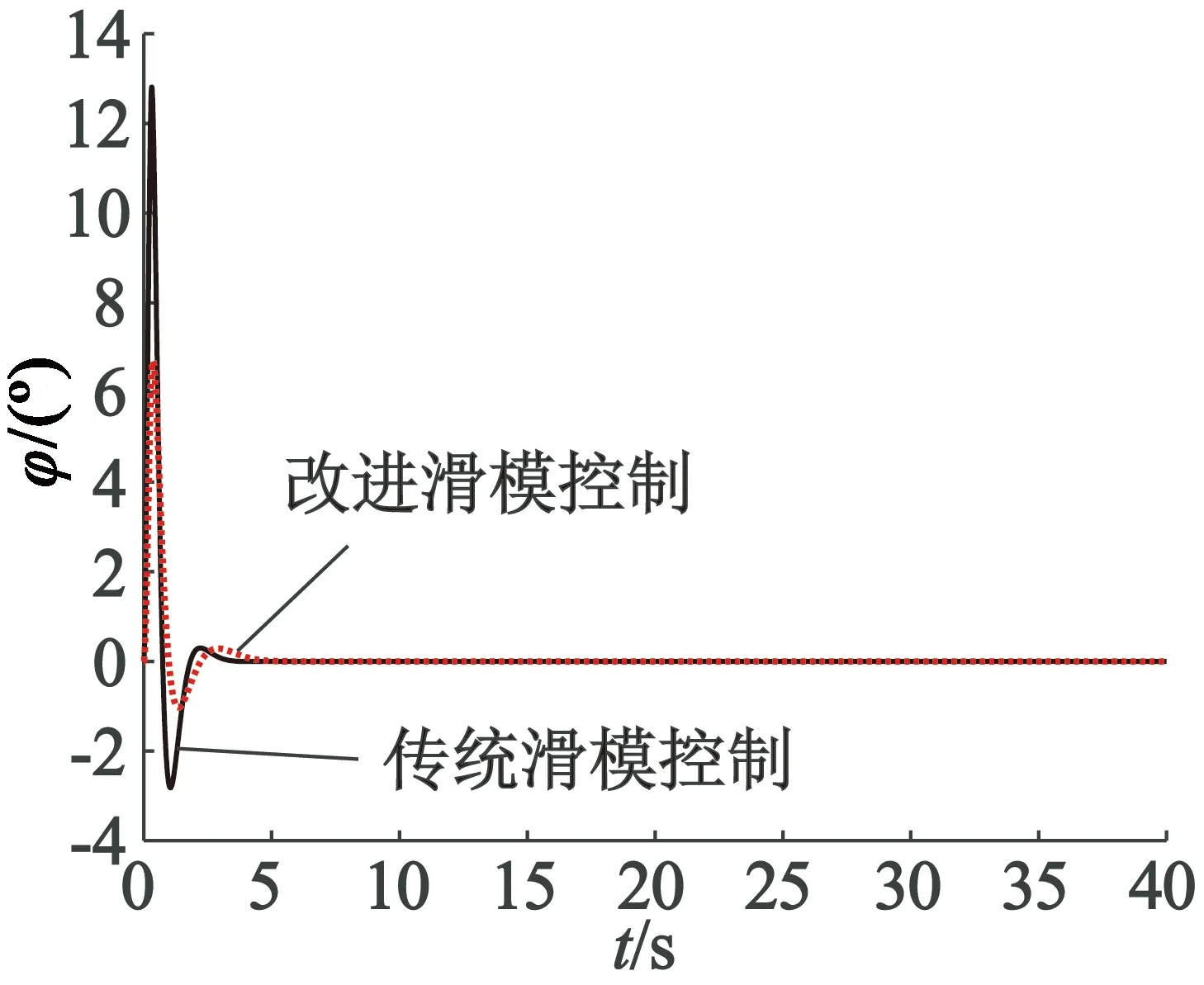
图3 滚转角响应曲线

图4 偏航角响应曲线

5 仿真结果分析

从图1的高度响应曲线可以看出，系统从初始状态到期望状态只需要5 s就可以实现，与传统滑模控制相比较，超调量较小，稳定性提高。图2为俯仰角响应曲线，图3为滚转角响应曲线，从图2、图3可以看出，只需要4 s，俯仰角和滚转角就能稳定地维持在期望的0。而图4的偏航角响应曲线说明系统也只需要5 s就能达到期望的50°，比传统滑模控制速度有所提高，并且能够一直保持稳定。

6 结 语

当系统存在扰动影响时，如果采用传统的控制律对飞行器进行控制，存在一定的缺陷。可通过提高控制器的性能，实现对四旋翼飞行器的姿态控制。本文在传统的趋近律滑模控制的基础上，对控制律做了一定的改进，并且进行了仿真分析。仿真结果表明，所设计的控制器能够有效地减小抖动，并实现了对期望的姿态实现稳定控制的要求。