高速永磁电机转子模态分析与实验研究

胡洪益，晏才松，曾 纯，申 政，刘龙辉

(中车株洲电机有限公司，株洲 412001)

0 引 言

高速永磁电机由于无励磁损耗、转速高、效率高、体积小、能直接驱动工作负载，被广泛用于智能制造、航空航天、现代交通等领域[1]。高速永磁电机转子通常采用表贴式转子结构，它是在永磁体外圆加保护套，护套分为合金护套和碳纤维护套两种。护套会使得电机气隙加大，增加磁钢用量。碳纤维护套工艺复杂，而合金护套表面会产生涡流损耗，降低电机的效率[2]。解决这些难题有效的方法是将磁钢进行内置，转子通过硅钢片叠压而成，永磁体插入硅钢片设计的磁钢槽中。

国内外学者对高速永磁电机转子模态分析做了大量研究工作。杨桃月[3]等针对高速表贴式转子进行了模态分析，计算了前8阶固有频率。卢南方[4]等针对高速永磁无刷表贴式转子进行了模态分析，然后通过模态实验验证了分析的准确性。而对于永磁体内嵌于硅钢片的转子结构，转子固有频率还没有精确的仿真分析方法。

本文以某高速永磁电机内嵌式转子(工作转速12 000 r/min)为研究对象，采用ANSYS有限元分析软件对转子进行自由模态分析，然后利用模态测试设备进行自由模态实验，结果表明，两者固有频率和振型相吻合，为高速永磁电机内嵌式转子动力学分析提供了参考依据。

1 模态分析

1.1 分析原理

高速电机转子动力学分析需要对转子-轴承支撑系统进行分析，转子模型的建模准确性对转子临界转速计算结果影响很大。转子在实际工况中受到轴承支撑等约束，边界条件比较复杂，有限元仿真分析困难。为了验证转子建模的准确性，对高速永磁电机转子进行自由模态分析，即不考虑支撑，使问题简化，可以了解转子振动的固有特性，为电机转子动力学优化提供参考依据。

动力学通用运动方程：

(1)

当转子为自由振动时并不考虑阻尼，即C=0，F(t)=0，发生谐振动时即位移x=Usin(ωt)时，则方程：

(2)

式中：M为质量矩阵，K为刚度系数矩阵且均已知，固有频率ωi和振型φi能从式(1)获得。从式(2)可以看出，转子固有模态频率和振型是由转子本身的质量以及刚度的大小决定。

1.2 有限元仿真分析

高速永磁电机内嵌式转子是由磁钢、磁钢楔紧块、转轴、硅钢片、压圈组成。转子通过硅钢片叠压成形，然后永磁体插入硅钢片磁钢槽中，硅钢片靠压圈压紧。转子各零部件材料参数如表1所示。

表1 转子各零部件材料属性

在UG软件中建立转子的三维模型，之后用ANSYS软件对转子模型进行自由模态仿真分析。因为计算转子自由模态，故不添加约束，计算前12阶自由模态固有频率，结果如图1所示。结果显示，前3阶固有频率接近0，这是转子在3个方向自由平移，4、5、6阶为转子在3个方向的自由转动，均为刚体模态，不是弯曲模态。通过振型判断7、9、11阶为前3阶弯曲模态，固有频率和振型如图2所示。

(a) 1阶弯曲振型(349.1 Hz)

(b) 2阶弯曲振型(711.8 Hz)

(c) 3阶弯曲振型(1 271.5 Hz)

2 模态实验

2.1 实验原理

(3)

对式(1)两边进行拉普拉斯变换，因系统的特性与初始值无关，所以初始值设为0，则有：

{s2M+sC+K}{X(s)}={F(s)}

(4)

式中：X(s)和F(s)为x(t)和f(t)的拉普拉斯变换，其中s=δ+jω为拉普拉斯变换因子，通过变换可以获得激励点的频响函数：

(5)

由式(3)得到的实测频响函数，输入输出信号经由分析系统对式(4)和式(5)进行相关变换，就可以获得转子各阶自由模态的固有频率和振型。

为了得到转子的固有频率，转子模态实验过程中要接近自由状态，转子的支承应尽量柔软。本文采用弹性绳悬挂的方式进行约束，悬挂点位于转子两轴承位置。该约束状态下,后续实验转子系统的刚体模态频率在10Hz以下，而转子1阶弯曲固有频率在100Hz以上。因此应用该支承方法进行转子系统自由模态实验是合理、可行的[4]。

2.2 实验方法

模态实验采用力锤对转子单点激励的方式进行激励，激励点不能选在模态振型的节点上，否则无法激发该模态振型。实验开始时要通过试敲来确定敲击点，确保前3阶弯曲模态都能激发出来。在力锤激励时，采集激励力以及各个测点的加速度响应来计算每个测点的频响函数，连续敲击3次，然后根据实测的频响函数来识别实验转子的模态参数。利用模态分析系统同步采集激振力和加速度的响应信号，计算得到频响函数。在获取整个模型的频响函数后，经分析给出结构的模态频率、阻尼和振型。模态测试及分析实验系统如图3所示。实验转子结构以及测点布置如图4所示。

图3 模态测试及分析系统示意图

图4 转子结构及测点布置图

2.3 结果分析

通过力锤单点激励测得实验数据，然后通过处理得到实测频响函数曲线，如图5所示。在经过初始估计的频响曲线上选取峰值点，得到其固有频率，取3次敲击实验平均值。实验值与仿真计算结果比较如表2所示。

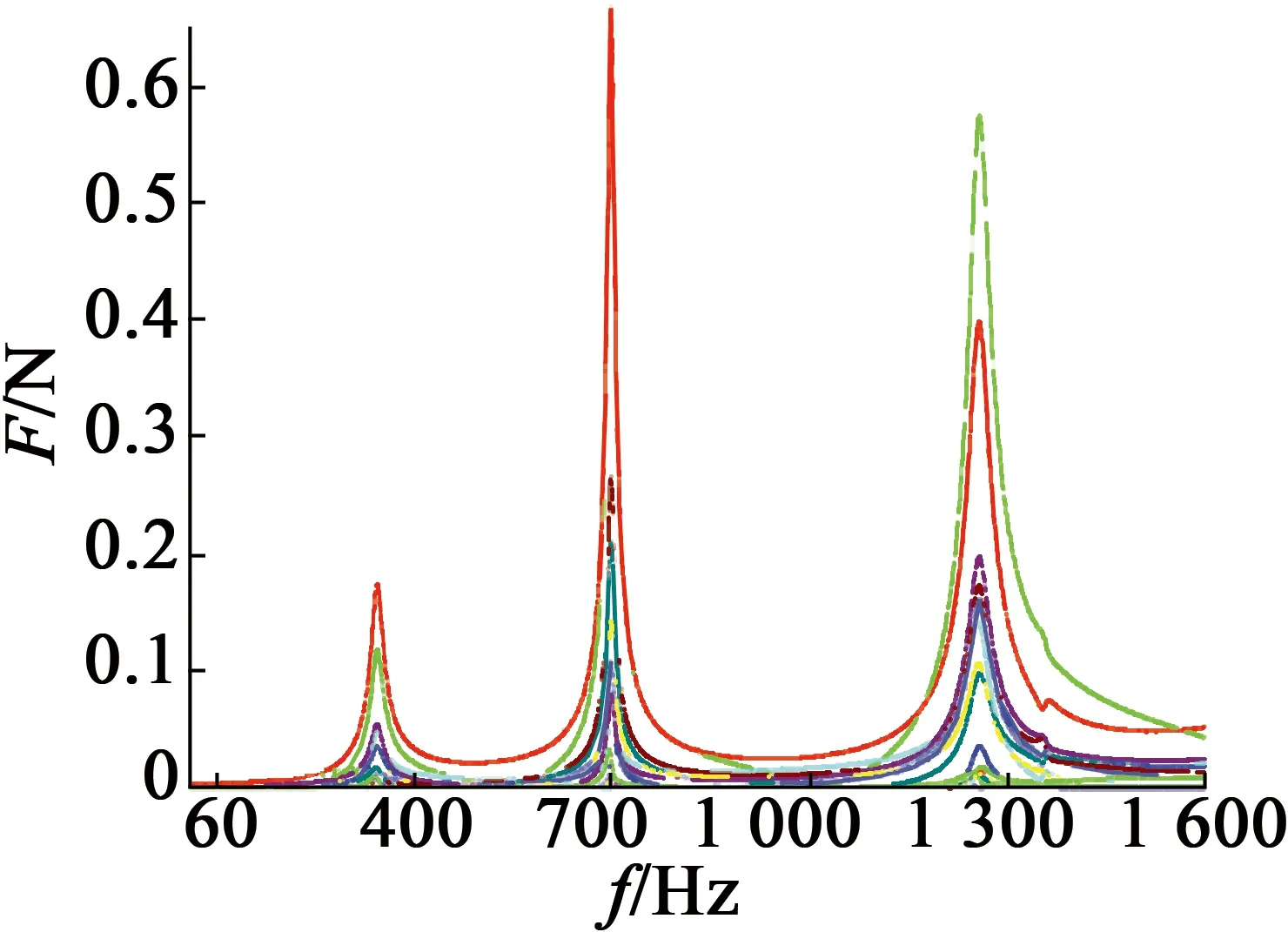
图5 模态实验得到的频响曲线

表2 计算模态和实验模态对比

阶次仿真值f1/Hz实验值f2/Hz误差Δf/%1阶349.1334.84.272阶711.8692.03.153阶1 271.51 257.21.13

比较表2转子仿真计算模态和实验模态频率值，最大误差为1阶4.27%，误差不大于5%，振型一致，验证了仿真计算的准确性，这对该类型的转子下一步动力学分析提供了参考依据。

3 结 语

本文针对某型高速永磁电机内嵌式转子(转速12 000 r/min)，采用UG软件进行三维建模，采用ANSYS软件进行自由模态仿真分析，通过计算获得了转子前3阶弯曲固有频率和振型。搭建了转子自由模态实验平台，得到了转子前3阶弯曲固有频率实验值，并与仿真值进行对比，验证了仿真计算的准确性，为同类转子设计动力学计算提供了参考依据。