次级非中心位置工况双边直线电动机有限元分析
2020-04-28陈玫志曾迪晖
吕 刚,陈玫志,杨 镜,曾迪晖,周 桐
(北京交通大学 电气工程学院,北京 100044)
0 引 言
从20世纪50年代以来,世界各国对直线电动机的研究日益深入。直线电动机在磁浮列车、直线电动机牵引地铁、飞机电磁弹射器、高层电梯等领域相继投入运行[1-3]。
在直线电动机的发展中,双边型直线感应电机是最先运用的一种类型,其优势是对称的结构和较大的推力。在理想运行条件下双边型直线感应电机次级处于电机中心位置,次级受到的法向力合力为零[4]。当运行于曲线行程或者受到振动等外部干扰时,初级会发生横向偏移,导致次级处于非中心位置。此时,由于结构和两侧气隙磁密的变化,法向力和推力均会发生相应的变化。非对称结构下的电机使得法向力对次级容易产生机械应力,导致了次级的形变。
相比于单边型直线感应电机[5-9],短初级双边型直线感应电机的研究较少,其为数不多的研究往往集中在对双边型直线感应电机进行一维、二维和三维的数值分析,也有对其不同初级、次级结构的研究[10-12]。但对双边型直线感应电机次级偏移的研究相对较少。然而,在实际应用中,往往偏移情况伴随着电机运行,偏移现象已成为一种“常态”。
本文主要对非磁性铝板次级的双边型直线感应电机进行了研究。首先,给出了次级处于非中心位置时,电机推力以及法向力三维有限元表达式,并解释了此时法向力不为零的原因,分析了法向力的性质。其次,通过建立双边型直线感应电机三维有限元模型,分析和计算了初级不同横向偏移时电机磁场、法向力和推力的变化;总结了一定横向偏移时,电机的法向力、推力与不同转差率的变化情况以及频率变化对电机法向力和磁场的影响。
1 双边型直线感应电机结构与特点
双边型直线感应电机次级结构与单边型的结构类似,有磁性、非磁性和复合次级等多种结构[13-16]。本文侧重于研究短初级直线感应电机在非磁性次级偏移情况下的电机特性。
典型的双边型直线感应电机应用如图1所示。次级采用导电性良好的非磁性铝板;两侧的初级由硅钢片和铜绕组构成。图1(a)表示正常工况下次级位于电机中心位置,两个初级和次级之间的空气气隙距离为g;图1(b)表示振动等外部因素引起初级偏移δ,即次级处于非中心位置时示意图。偏移导致电机结构不对称,电机力特性会发生显著变化。
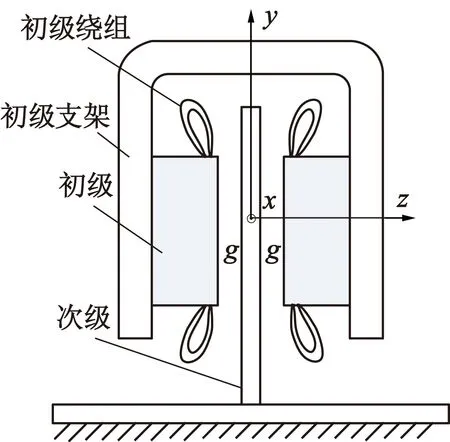
(a) 次级中心位置

(b) 次级非中心位置
2 直线感应电机数值分析
由于初级电流没有z方向分量,故磁动势只有x和y方向分量,即Az=0,由B=×A得:
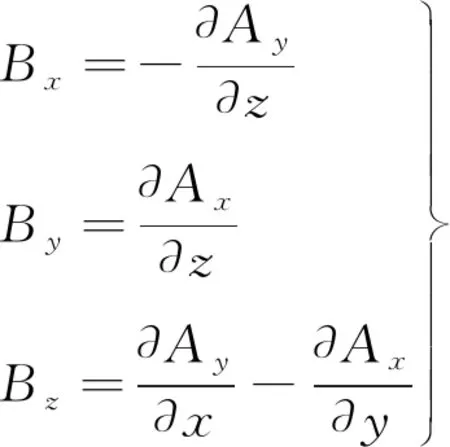
(1)
计入涡流的整个求解域的电磁方程:
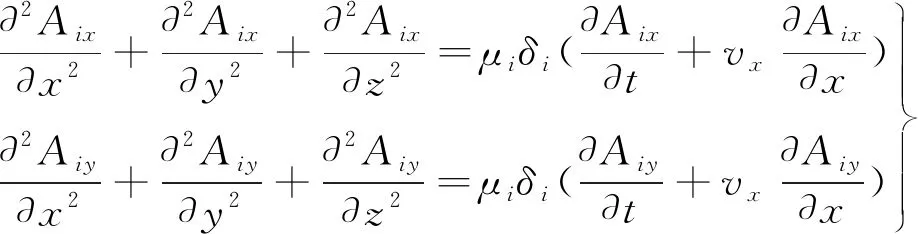
(2)
式中:下标x,y,z,i分别表示x,y,z分量和求解区域编号。求解区域1~4分别表示初级铁心、绕组、次级铝板、气隙,且在每个求解区域内有:
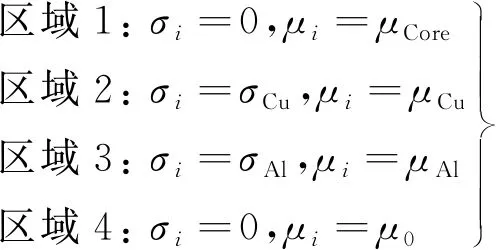
(3)
式中:μCore,μCu和μAl分别为铁心、铜和铝的磁导率;μ0为空气磁导率;σCu为铜的电导率;σAl为铝的电导率。
假设次级铝板的总剖分数为n,则其获得的推力Fx:

(4)
式中:下标j为第j个剖分单元,Jyj和Vj分别为对应剖分单元的初级电流密度的y向分量和单元体的体积;Te为计算周期。
由图2可知,两侧初级所受的法向力分别:
(5)

(6)
式中:Bxj1,Byj1为次级左侧表面的磁感应强度的x方向分量、y方向分量;Bxj2,Bxj2为次级右侧磁感应强度的x方向分量、y方向分量。由力的相互作用可知次级所受法向力大小:
Fz=F1-F2
(7)
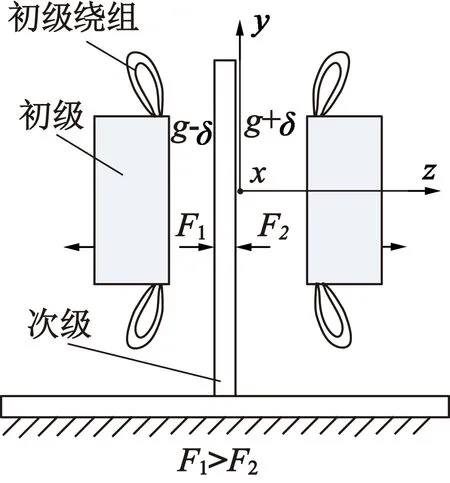
图2 双边型直线感应电机次级偏移时法向力
3 三维有限元分析
为研究不同偏移、频率下双边型直线感应电机的力与磁场特性,建立电机三维有限元分析模型如图3所示,电机参数如表1所示。

图3 三维双边型直线感应电机模型
表1 双边型直线感应电机参数
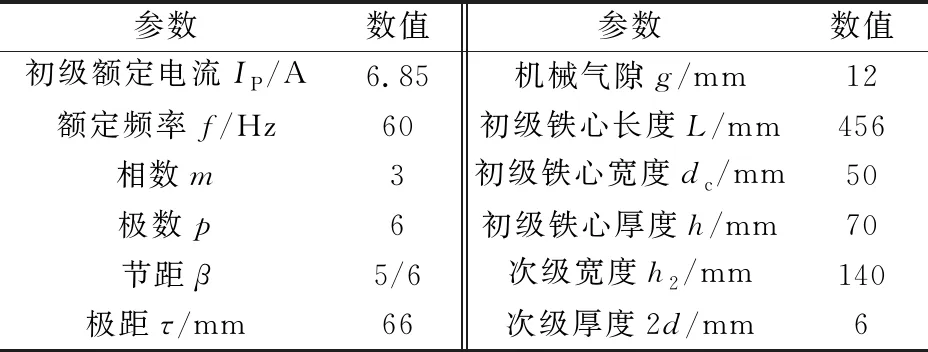
参数数值参数数值初级额定电流IP/A6.85机械气隙g/mm12额定频率f/Hz60初级铁心长度L/mm456相数m3初级铁心宽度dc/mm50极数p6初级铁心厚度h/mm70节距β5/6次级宽度h2/mm140极距τ/mm66次级厚度2d/mm6
3.1 同频率且不同偏移下电机磁场和力特性分析
图4是电机高速运行时双边型直线感应电机次级上表面的磁场、涡流分布图,其中频率60 Hz,额定电流6.85 A,转差率s=0.6,偏移0或6 mm,运行时间0.02 s。由于次级下表面磁场特性变化不明显,所以不再讨论。纵向边端效应使得入端和出端磁场发生畸变,当电机初级发生偏移时,次级表面的磁场空间分布未发生较大变化,磁场强度增加。次级发生偏移时,导致电机对称结构发生变化,靠近初级侧磁场强度明显增大。
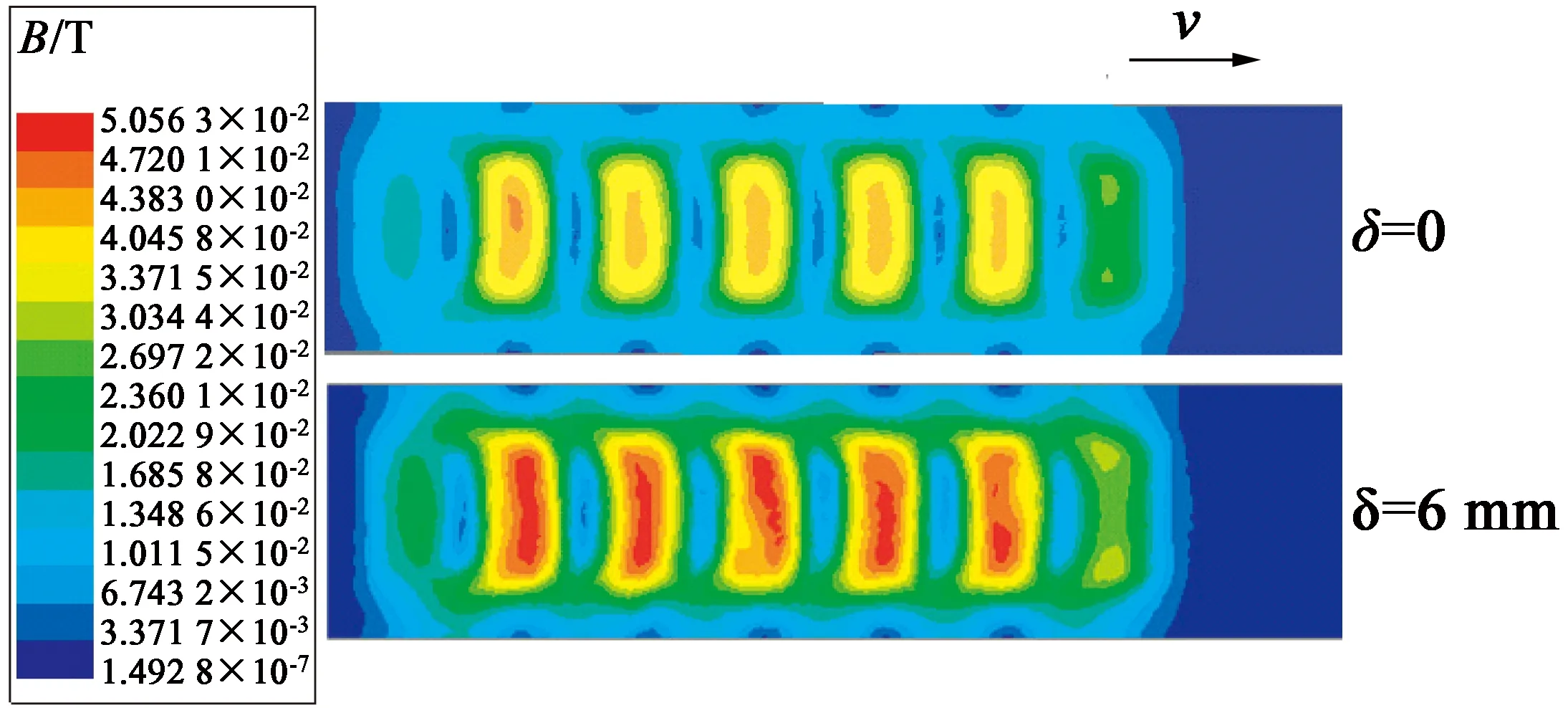
(a) 磁场变化
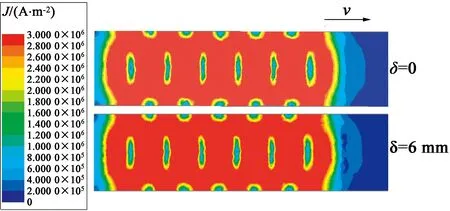
(b) 涡流变化
当研究初级不同偏移下的电机磁场特性时,选取额定工况下频率60 Hz,额定电流6.85 A,转差率s=0.6。如图5所示,当初级分别偏移0、4 mm、6 mm、8 mm时,纵向、横向气隙磁密都依次有所下降。相比于中心位置,偏移4 mm时磁场强度下降4.63%,偏移6 mm时磁场强度下降7.32%,偏移8 mm时磁场强度下降9.35%。偏移导致气隙磁密减小,进而影响推力和法向力。
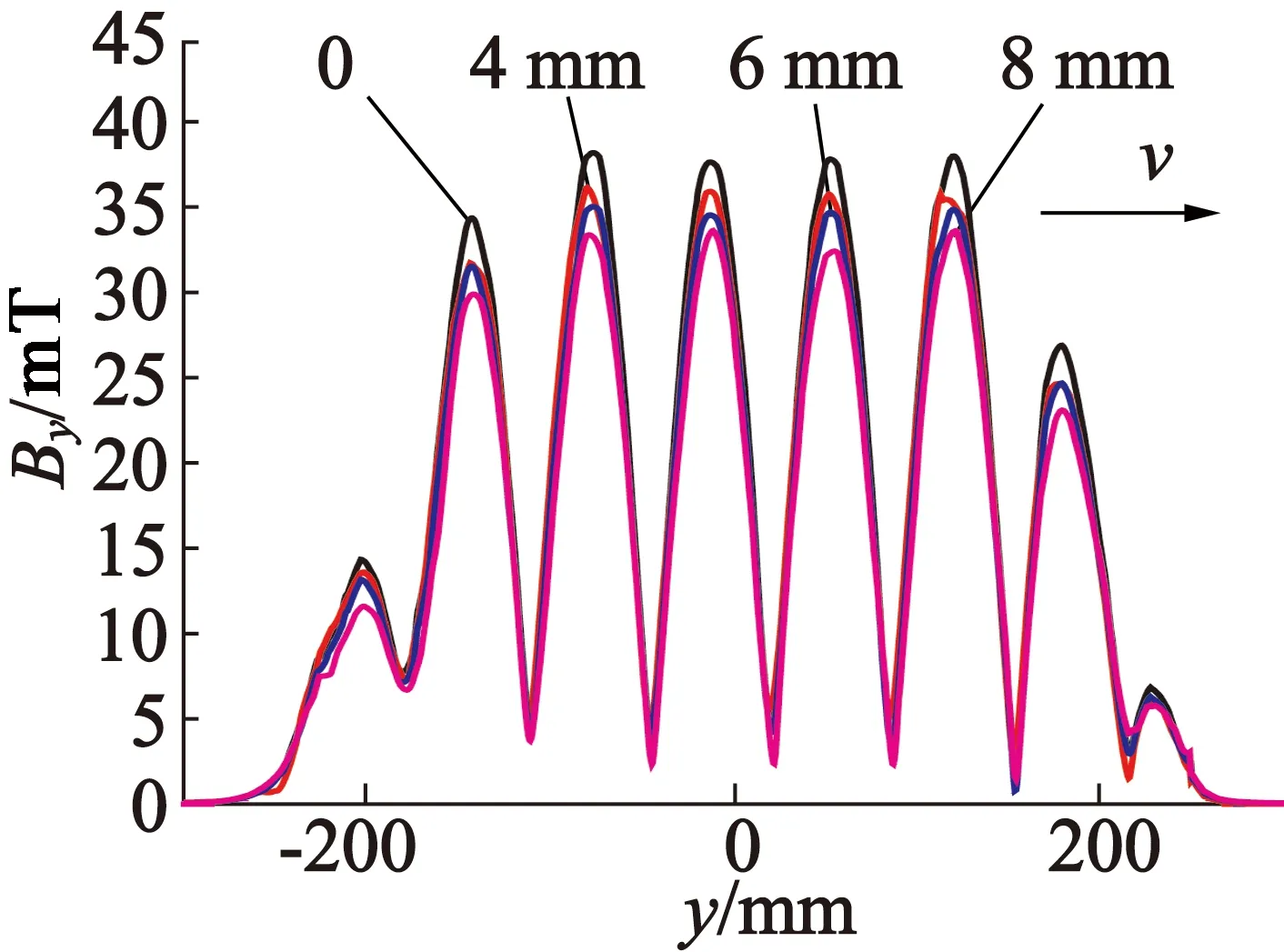
(a) 纵向磁场
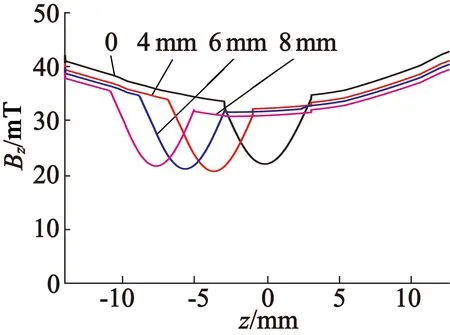
(b) 横向磁场
现研究不同偏移下法向力变化规律。额定工况下,当频率60 Hz,电流6.85 A时,选取s=0.6时双边型直线感应电机法向力瞬时变化曲线作为研究对象。如图6所示,当初级不发生偏移时电机法向力合力为0;当初级偏移4 mm、6 mm、8 mm时,随着偏移量的增大,法向力最终稳定值逐步增大。通过观察法向力波动曲线可以看出,随着偏移的增大,法向力瞬态响应波动也逐渐增大。偏移4 mm时,法向力幅值波动3.2%;偏移6 mm时,法向力幅值波动4.3%;偏移8 mm时,法向力幅值波动8.3%。显然,偏移增加了电机的振动,对电机的机械性能影响是不利的。
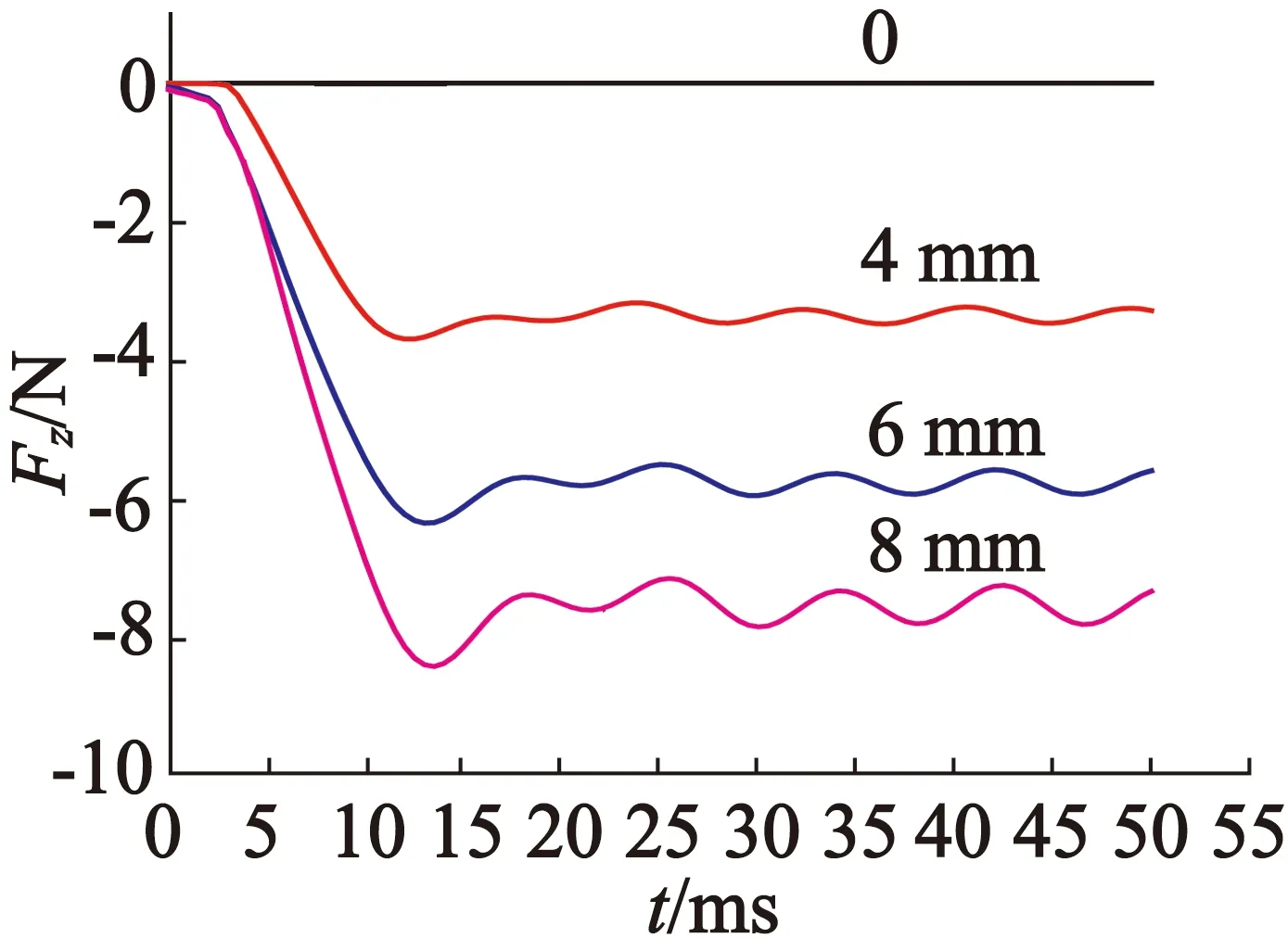
图6 双边型直线感应电机初级偏移时法向力变化
图7是不同偏移下法向力随转差率变化趋势图。额定工况下,当频率60 Hz,电流6.85 A时,在偏移4 mm、6 mm、8 mm下,随着转差率s逐渐增大,作为恢复力的法向力呈现增大的趋势。当考虑采用双边型直线感应电机驱动的运动装置时,次级板的机械硬度应该要能够承受次级最大偏移程度下法向力的作用并且保有一定的余量,从而保证电机运行的安全性。

图7 双边型直线感应电机偏移时法向力随转差率变化
当频率60 Hz,电流6.85 A时,研究偏移量为0、4 mm、6 mm、8 mm时非磁性次级下双边型直线感应电机推力变化。如图8所示,随着转差率s的增大,推力先增大后减小。在转差率s=0.6附近,电机推力取得最大值。随着偏移量增大,推力逐渐增大。这是由于随着初级偏移量的增大,次级越靠近初级绕组时磁场越大,且穿过次级磁通越大,从而使得推力增大。
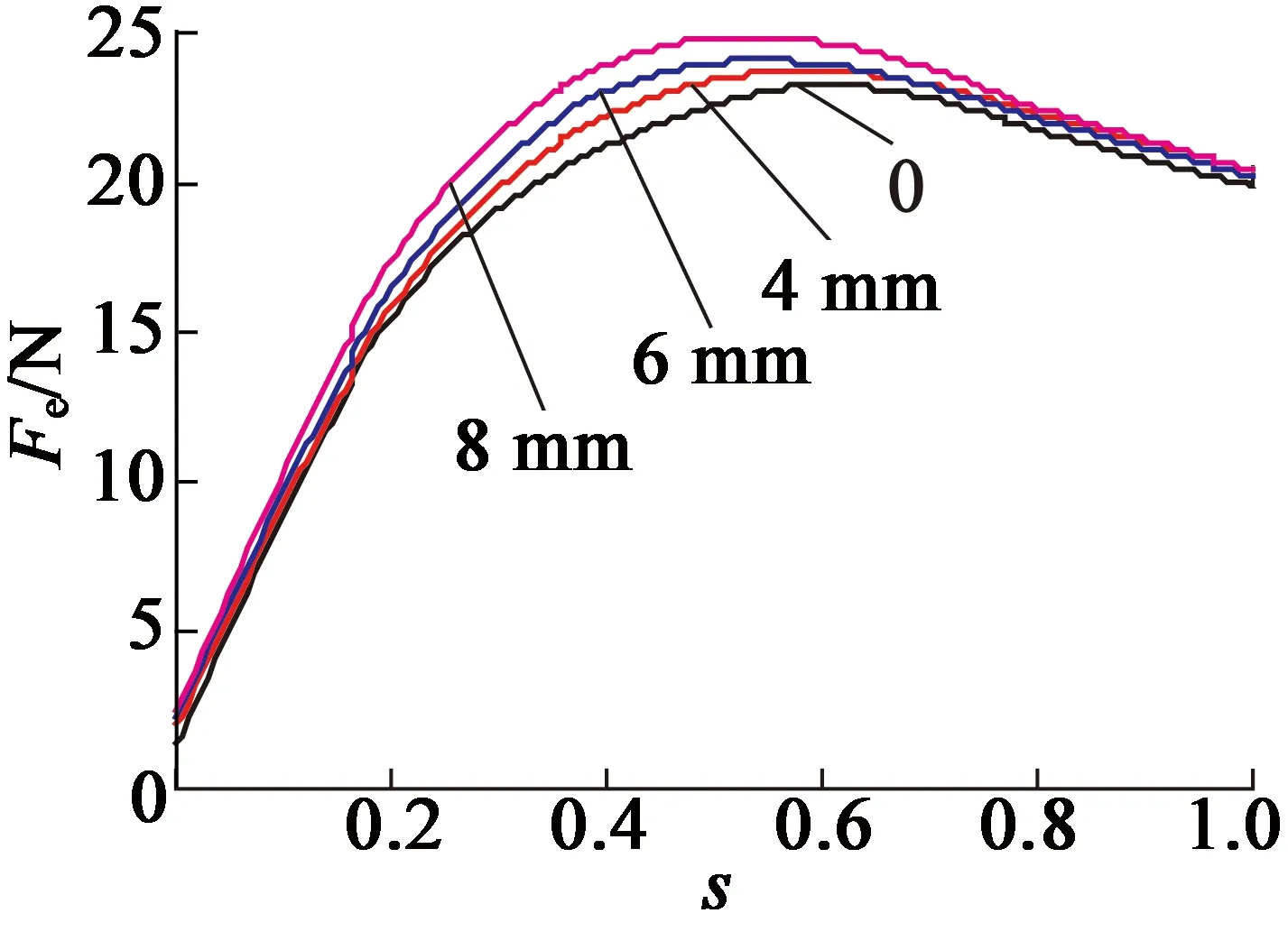
图8 不同初级偏移下电机推力随转差率变化
3.2 频率变化对直线电动机力与磁场的影响
主要研究当供电频率发生变化时,电机偏移情况下,采用铝板作为次级时双边型直线感应电机力与磁场的特性。
额定电流6.85 A,转差率s=0.6,频率40 Hz、60 Hz、80 Hz时,双边型直线感应电机在偏移6 mm时纵向、横向气隙磁场分布如图9所示。频率大于40 Hz时,随着频率的增加,磁场是下降的。当频率由40 Hz变为60 Hz时磁场强度降低9.4%;频率由60 Hz变为80 Hz时磁场强度降低7.9%。气隙磁场减小使得推力减小,当电机高速运行时需要根据实际情况选择合适的频率,以使电机能够输出足够的推力。
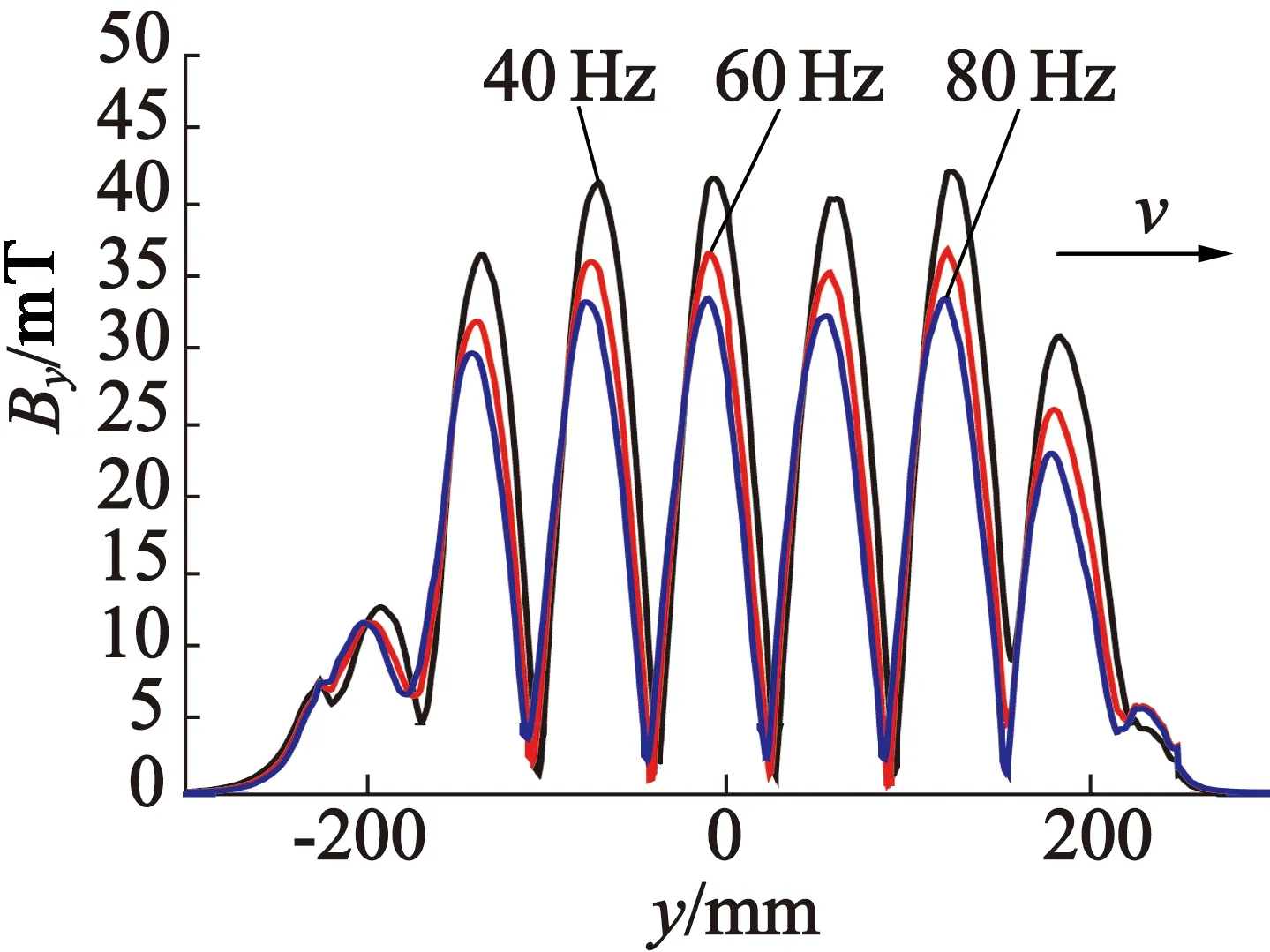
(a) 纵向磁场

(b) 横向磁场
偏移量8 mm,额定电流6.85 A,转差率0.6,频率为40 Hz、60 Hz、80 Hz时双边型直线感应电机法向力变化趋势如图10所示。随着频率的增加,相同速度下法向力是增加的。以速度为0时的法向力为例,40 Hz到60 Hz时法向力增幅23.5%,60 Hz到80 Hz时法向力增幅9.6%。由此说明,电机运行时需要根据频率曲线,合理控制偏移时法向力大小。
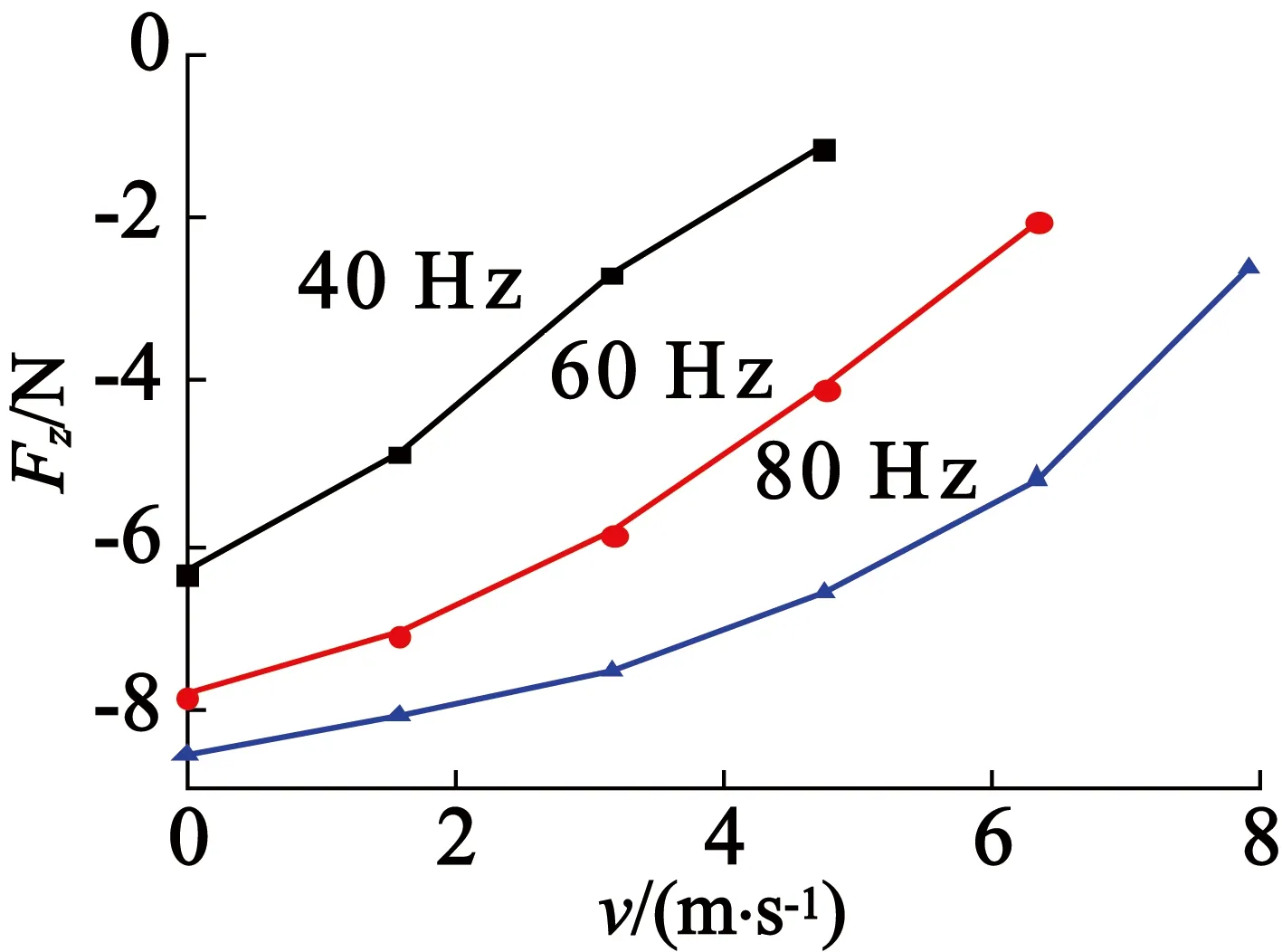
图10 不同频率下双边型直线感应电机法向力变化
4 结 语
本文通过对双边型直线感应电机次级偏移时力和磁场特性进行分析研究。首先介绍了双边型直线感应电机应用场景,接着运用三维理论对其进行解析计算,最后通过三维有限元仿真对双边型直线感应电机偏移进行分析。总结如下:
1)双边型直线感应电机在初级发生偏移时,次级板不再位于电机中心位置,导致次级法向力不再对称,从而表现出法向力不为零。当次级偏移气隙中央位置6 mm时,法向力增加到约为推力的23%。
2)非磁性次级产生的法向力抑制初级偏移,是一种恢复力,增加电机的运行稳定性。偏移越大,恢复力越大。
3)随着偏移量的增大,次级靠近初级绕组时磁场增大且穿过次级磁通增大,使得双边型直线感应电机推力可增加大约9%。
4)在一定偏移下,随着频率的增加,法向力是增加的。为避免次级板受力过大,电机运行过程中需要根据频率和法向力关系曲线选取合适的运行频率。
