让抽象的概念“活起来”

【摘 要】深度思维不仅有助于学生深刻理解数学本质，深入探寻知识间的密切关联，更能让他们在研究中积累数学活动经验，实现数学思考，提升数学素养。在教学中，教师可以通过制造认知冲突、搭建认知场域、提供创造舞台等策略，引导学生在深度思维的过程中把握概念本质、理解概念内涵、形成概念结构、活化概念理解。

【关键词】深度思维;确定位置;认知冲突;认知场域;创造舞台

【中图分类号】G623.5【文献标志码】A【文章编号】1005-6009（2020）17-0062-05

【作者简介】赵国防，江苏省无锡通德桥教育集团（江苏无锡，214000）总校长，高级教师，江苏省数学特级教师，江苏省“333高层次人才培养工程”培养对象，江苏省网络名师工作室领衔人。

【背景】

认知理论认为，概念形成一般要经历感知活动、思维加工、理解应用、形成结构四个步骤。概念教学自然应让学生充分经历概念形成的全过程。然而，在实际教学中，思维加工和形成结構这两个重要环节常常被忽视。如此，学生对概念的理解就会浮于表面，只知道它“是什么”，却不知道“为什么”与“从哪儿来”等深层次问题，其间应有的思维训练更无从谈起。

数学是思维的体操。概念教学自然也应担负起思维训练的重任。在教学中，教师要在深入研究教材和学生的基础上，积极开发有利于概念形成与发展的宝贵资源，用核心问题引导学生深度思维，使他们充分经历大量的感知活动，并在此基础上进行思维加工，积极投入应用与创造之中，最终形成概念结构，突出深刻理解与系统建构。只有这样，才能真正实现概念形成的系统化、结构化与深刻化，让概念教学立足概念、发展概念、超越概念。

就苏教版四下《确定位置》一课来说，新概念无疑就是“数对”。作为表示物体位置的概念，数对既是数形结合的有力体现，也是数学符号化与简洁性的生动诠释，还是一种量化表达二维空间中物体位置的重要方式。因此，在本课教学中要努力做到以下三点：一是要立足生活，关注生活，更要超越生活，凸显数学规范。如“座位图”既易受观察者方向的影响，又易受生活实际的局限，在教学中应当慎用、巧用;二是要延展概念形成过程，强化深度思维与系统建构，适度凸显“定位点”之间关系的探索与发现。这样可在适当渗透坐标与函数思想的基础上，让学习得以延伸;三是顺应儿童认知规律，遵循由块到点、由点到线的认知逻辑，在逐步抽象的过程中延展思维，深刻内化，让“确定位置”不只是“定位”，更是在渗透函数思想。基于以上思考，在泉州师范学院苏明强教授的指导下，笔者对本课进行了以下探索与实践。

【教学过程及分析】

一、制造认知冲突：只有“列”可不行

师：同学们，我在黑板上画一个点，这个点表示0。我再画一个点，这个点表示1。再在它后面画一个点，这个点表示几呢？

生：2。

师：对，再画一个点呢？

生正要说3，此时教师却点在了比3还靠后一点儿的位置。

生：4……

师：啊？！不是3吗？

生（摇头，并信心满满地）：你空过了3，从间隔的距离来看，肯定是4。

师：真会观察和思考！

师：是的，3在这里呢。（说着出示点3）4的后边是几呢？

生：5，6，7……

师：对，一直画下去，能画完吗？后面还有好多好多数呢。

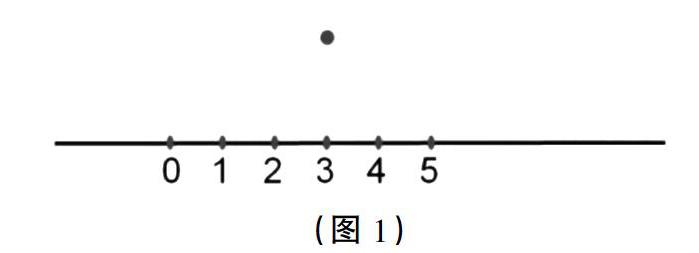
师：请大家仔细看黑板，见证奇迹的时刻到了！（点了一个点，形成如图1所示的板书）

学生一片安静，瞪着眼睛在琢磨着……

生：是3，我看它和3齐着！

师：你们认为呢？

生（齐答）：应该是3。

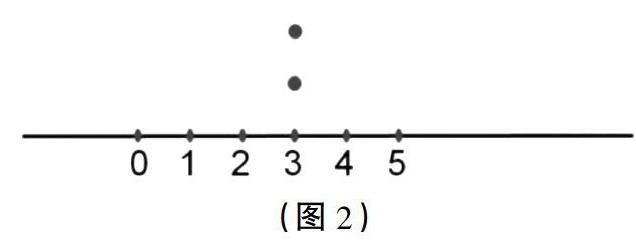
师：好吧，听你们的，暂且看作3。那再画一个点（如图2）呢？还是3吗？

生：啊？！不对，都是3就乱套了，我看它们都在一列上呢。

师：哦？都在哪一列上呢？

生：都在第3列上。

师：是的，它们都在第3列上。

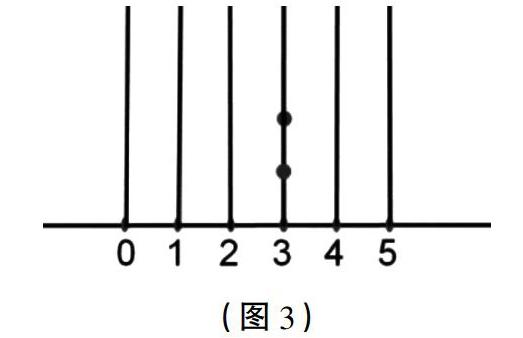
教师顺势揭示“列”。（如图3）

师：那如果只有“列”，你能清楚地表达这两个点的位置吗？

生：就是呢！我一直在琢磨，它们虽然都在一列上，但位置明显不同啊……

把握要点，直面困惑。“数对”教学有两个重要的知识点：一是“先数列，再数行”;二是“确定第几列，要从左往右数;确定第几行，要从前往后数”。这两点仿佛成了一种理所当然的“规定”，常常被教师“硬塞”给学生。一节课下来，对于“为什么要这样数”，学生则是一片茫然。面对这种传统教法的尴尬，笔者精心设计，引导学生在常规表达中“遭遇”挑战，在数数中体会到“列”的由来。

聚焦本质，经历过程。“数对”这一概念实际上是一种对二维空间物体位置的量化表达。它既是一种量化过程的概括，也是一种量化结果的提炼。如果仅仅停留在记忆层面，学生只会用，但不能真正理解这一概念的本质。在教学中，笔者努力延展概念形成的过程，引领学生充分经历从一维空间到二维世界的建构过程，深切体会到一定要先数“列”，并从真实经历中悟到了“为什么要这样数”。

制造冲突，激活思维。矛盾是事物发展的动力。学生的深度学习也充满了矛盾和冲突。教材现成的“座位图”这一情境固然形象、直观，但为了充分唤醒学生已有的学习经验，引导他们在实际运用过程中经历原有认知和所面临的新问题之间的“冲突”，诱发深度思维，笔者进行了创新设计。这样设计主要基于三个方面的考虑：一是让现成的素材活起来，便于学生经历概念形成的完整过程;二是引导学生经历“碰壁”过程，激活深度思维;三是与之前的数数巧妙对接，让新知学习寻得“系统关联”，体现深度学习的重要特征。

二、构建认知场域：“数对”原来如此好玩

1.建立“数对”概念。

师：那怎么办呢？

生1：一個点离3很近，一个点离3远一点。

生2：它们都在一列上，但不在一行上。

师：你说到了“行”，哪里有“行”啊？

生2：我们座位里就有“行”，我在第2行。

生3：对，我知道了，一个点在第1行，一个点在第2行。

师：咦，说得有点道理嘛！但我没看到“行”啊？谁来指一指哪里有“行”？

学生上台指，教师顺势揭示“行”。（如图4）

师：现在你能分别说说这两个点的位置吗？

生：一个点在第3列，第1行;另一个点在第3列，第2行。

师：好，说得不错！再给你两个点（如图5），你能快速说说它们的位置吗？

生：一个点在第2列，第4行;另一个点在第5列，第5行。

师：说得对吗？你能说说你的秘诀吗？

生：我先看它在第几列，再看它在第几行。因为老师标了列数和行数，所以读起来很快。

师：方法总结得不错！刚才我们学会了用列数和行数来表示一个点的具体位置，但在表达这个点的位置时需要说一句较长的话才能讲清楚。数学本身具有简洁之美，你能开动脑筋，让这句长话变得简洁一些，体现简洁之美吗？自己试一试。

生1：2列，4行。

生2：2和4。

生3：2;4。

生4：2，4。

…………

教师顺势揭示“数对”，并强调书写的规范和要求。

2.发现“数对”秘密。

师：我们来回顾一下刚才的探索过程，给你一分钟时间，看一看，还有哪些重大发现？

生：我发现刚刚两个点的数对里都有3，一个是（3，1），一个是（3，2）。

师：哦？对，为什么会都有3呢？

生：数对的第一个数表示列，它们都在第3列上，所以肯定第一个数都是3。

师：同意他的说法吗？

生（齐答）：同意！

生：我还发现有一个点的数对有两个5。大家可不要以为它们是一样的5啊，第一个5表示的是第5列，而第二个5表示的是第5行。

师：你的发现和提醒很有见地！

生：我还发现，不管是哪个点，要表示它的位置，必须要用两个数，一个数表示列，一个数表示行，缺一不可。

师：他总结得怎么样？谁来评价一下？

生：总结得很到位，他把数对的本质一语道破了。

…………

问题驱动，让学习充满挑战。仅有“列”，已经无法解决当下的问题了，学生在“山重水复疑无路”时，思维高速运转，“行”应运而生，大有“柳暗花明又一村”的畅快。这样一来，不仅引导学生实现了从一维空间到二维空间的升级，而且让他们深切感悟了概念形成的完整过程。数对为什么要用两个数来表示？这两个数分别代表什么意义？这一系列问题，学生在过程经历中自然解决了，不仅印象深刻，而且妙趣横生。

提炼概括，让数学彰显简洁美。概念教学不仅要引导学生经历概念形成过程，更要及时引导学生进行提炼与概括。笔者放手让学生在概括第几列、第几行的表达方式时一步步抽象与简化，在体验活动中深切感悟“数学好玩”“数学好美”。

反思回顾，让思维走向深刻。学习的过程需要“一路向前”，更需要及时“回头看”，即反思与回顾。笔者通过引导学生进行反思与回顾，将学生对数对内涵与外延的理解带上了一个新的高度，也切实培养了他们善于反思与回顾的良好学习习惯，训练了他们的深度思维，使他们的空间观念和空间想象能力得到了发展。

三、提供创造舞台：“数对”背后居然有这么多秘密

教师出示“探索活动”：

1.标一标：用数对标出长方形（如图6）四个顶点的位置，并说说自己的发现。

2.移一移：将长方形向右平移一格，画出平移后的图形，并用数对标出四个顶点的位置。

3.说一说：通过对比平移前后各个顶点的数对，你有什么发现？

学生自主活动后汇报。

生1：通过“标一标”和“移一移”，我发现这里边有好多秘密呢！首先是标完四个点的数对（如图7）后，我就发现，在同一列上的点，数对的第一个数都相同;在同一行上的点，数对的第二个数都相同。然后，我就运用这个原理迅速标出了向右平移一格后长方形四个点的位置（如图8），技巧是每个数对的第一个数都加1。

师：为什么每个数对的第一个数都加1啊？

生1：四个点都向右平移，就说明在行没变的情况下列数都增加了1，而数对的第一个数表示列，所以每个数对的第一个数都加1。

师：他的回答你听明白了吗？

学生齐答听明白了，并不约而同地鼓掌。

师：谁还有其他发现？

生2：我是横着看的，发现平移前后每一行上四个点的数对的第二个数都没变，谁知道这是为什么呢？

生3：我知道，因为是在固定的行上平移的，平移前后行数当然不会变。又因为数对的第二个数表示行数，所以它们当然不会变了。

生4：老师，我觉得长方形每条长边就像在一条长长的直线上滑行。

师：“在一条长长的直线上滑行”，说得真好！每一行上的四个点确实都在一条直线上。谁还有问题？

生5：我还有问题，刚刚是向右平移一格，那现在再向上平移两格，四个点的数对又该怎样表示呢？

师：他提出了一个极具思维含量的好问题！下面，请大家再仔细看一下现在长方形的位置，然后闭上眼睛想象它向上平移两格的过程，平移结束后用数对表示四个顶点的位置。想好的，可以睁开眼睛。

生：这个太简单了！向上平移，列数不变，即数对的第一个数不变，只把每个数对的第二个数加2即可。

师：啊？！为什么要加2？

生：向上平移两格，行数增加2，数对的第二个数肯定要加2。如果向下平移两格，行数便会相应地减2。

师：大家都是这么想的吗？学数学，就是要学会多角度地思考和审视问题，善于发现规律、运用规律。数学，奥妙无穷！思考，无处不在！

…………

打破传统练习局限，关注综合能力提升。只有通过充分而必要的具体应用，才能促进概念的理解应用和结构形成。在教学中，笔者设计了一组兼具综合性、实践性、开放性与挑战性的“探索活动”，引导学生在“标一标”“移一移”“说一说”的活动中，多角度面临挑战，全领域接受考验，数对的内涵及外延自然而然内化于心，并通过现实情境及时外化于行，他们的观察、思考、分析、概括、表达等能力都得到了一定程度的提升。

聚焦概念本质，促进深度思维。概念教学的每个环节都应牢牢抓住“概念建构与理解”这条“明线”，千方百计地引导学生在概念建构与理解过程中实现“思维训练”这条“暗线”的教学目标。在“移一移”和“说一说”的过程中，学生的思维被彻底打开，多角度观察问题、思考问题的能力与意识自然得到了提升，思维的灵活性与广阔性得到了充分训练，概念的本质与内涵得到了强化理解与自然应用。“长方形每条长边就像在一条长长的直线上滑行”，这虽是学生的一种想象，但渗透了学生对各点所在的“线”的特征的理解，更渗透了函数思想，实为数学思想的又一次深切体悟与超越。

关注问题提出，重视数学思考。提出问题不仅是探究与发现的需要，更是学生深度思维的前提与基础。没了问题，就没了真正意义上的研究。上述环节，结合活动进程，笔者及时鼓励学生说出自己的发现，实际上就是在刺激他们的思维，给他们创造发现问题与提出问题的机会及可能。“再向上平移两格，四个点的数对又该怎样表示呢？”这个来自学生的真实问题，向全体学生提出了新的挑战，使他们的数学思考自然“升级”。