A helium stratified and ingassed lower mantle: resolving the helium paradoxes

· ·

Abstract It is generally believed a variation of 3He/4He isotopic ratios in the mantle is due to only the decay of U and Th,which produces 4He as well as heat.Here we show that not only 3He/4He isotopic ratios but also helium contents can be fractionated by thermal diffusion in the lower mantle. The driving force for that fractionation is the adiabatic or convective temperature gradient, which always produces elemental and isotopic fractionation along temperature gradient by thermal diffusion with higher light/heavy isotopic ratio in the hot end. Our theoretical model and calculations indicate that the lower mantle is helium stratified, caused by thermal diffusion due to ～400 °C temperature contrast across the lower mantle. The highest 3He/4He isotopic ratios and lowest He contents are in the lowermost mantle, which is a consequence of thermaldiffusion fractionation rather than the lower mantle is a primordial and undegassed reservoir. Therefore, oceanicisland basalts derived from the deepest lower mantle with high 3He/4He isotopic ratios and less He contents—the long-standing helium paradox, is solved by our model.Because vigorous convection in the upper mantle had resulted in disordered or disorganized thermal-diffusion effects in He,Mid-ocean ridge basalts unaffected by mantle plume have a relatively homogenous and lower 3He/4He isotopic compositions. Our model also predicts that 3He/4He isotopic ratios in the deepest lower mantle of early Earth could be even higher than that of Jupiter, the initial He isotopic ratio in our solar system, because the temperature contrast across the lower mantle in the early Earth is the largest and less 4He had been produced by the decay of U and Th. Moreover, the early helium-stratified lower mantle owned the lowest He contents due to over-degassing caused by the largest temperature contrast. Consequently,succeeding evolution of the lower mantle is a He ingassed process due to secular cooling of the deepest mantle. This explains why significant amount of He produced by the decay of U and Th in the lower mantle were not released, another long-standing heat–helium paradox.

Keywords Helium paradox · Thermal diffusion · Mantle convection · Adiabatic temperature gradient · Primordial mantle · Ingassed lower mantle

1 Introduction

The driving force for mass diffusion is the difference or gradient of chemical potential(Lasaga 1998;Zhang 2008),which can be produced by many natural processes,such as the decay of radioactive elements, electricity, and magnetism, chemical reaction, melting and crystallization,immiscibility in melt and mineral, etc. In many natural systems, original driving force for mass diffusion is temperature difference or gradient. For example, temperature gradient can cause chemical gradient, and thus producing chemical and isotopic differentiation in silicate melt(Huang et al.2010;Walker and Delong 1982),in Fe–Ni–S melt (Brenan and Bennett 2010), and in crystalline solid(Asaro et al.2008;Korte et al.1997).The chemical effects caused by temperature gradient are also called the Soret effect or thermal diffusion.Mantle convection can generate temperature gradient, which is termed adiabatic or convective temperature gradient(McKenzie and Bickle 1988).The chemical differentiation or inhomogeneity made by convective temperature gradient in the mantle is expected to be zero, however, because mantle convection tends to wipe out this differentiation due to diffusion of most components in the solid mantle are extremely slow(Chakraborty 2010).

However, the diffusivity of Helium is very fast in the solid mantle (Cherniak and Watson 2012), given the small atom size and inert nature of He. The diffusion coefficient of helium in olivine is ～1.36 × 10-11m2/s at the bottom of the upper mantle (14 GPa and 1527 °C) (Wang et al.2015). Hence, the corresponding characteristic diffusive distance is 2.1 cm in 1 year, which is much smaller than the average convective velocity of upper mantle, e.g.,20 cm/year (Weismueller et al. 2015), but faster than that of the lower mantle, e.g., 1.5 cm/year (Butterworth et al.2014). Probably, the chemical and isotope effects of He caused by the adiabatic temperature gradient in the convective mantle are expected to be present in the lower mantle and absent in the upper mantle.

In this paper,we first describe two issues or‘paradoxes’related to mantle helium. One is the ‘‘He concentration paradox’’ (Anderson 1998), the other is the ‘‘heat–helium paradox’’ (Onions and Oxburgh 1983). Second, we performed numerical experiments to demonstrate that the Soret effect of helium is working in the lower mantle.Accordingly, we quantitatively develop a model to theoretically analyze elemental and isotopic behaviors of He in mantle rock when imposed a temperature gradient.Finally,we applied our model to solve the two paradoxes and relevant issues are discussed.

2 The helium paradoxes

Helium has two isotopes3He and4He.3He in the mantle was probably made during the Big Bang, and is called the primordial isotope(Anderson 2007);while most4He in the mantle are produced by α-particle (4He) decay of238U,235U, and232Th decay series. Consequently, the4He/3He ratio in the mantle is a function of the time-integrated(U + Th)/3He ratio (Class and Goldstein 2005), and reservoirs with high3He/4He ratios are usually assumed to be primordial, undegassed or unprocessed, stored in a convectively isolated lower mantle (Tolstikhin and Hofmann 2005;van Keken et al.2002).Mid-ocean ridge basalt(MORB) and oceanic island basalt (OIB) are derived from the upper and lower mantle, respectively (White 2015).Accordingly, the rare gases of MORB and OIB are good tracers of mantle chemical structure and evolution(Mukhopadhyay and Parai 2019). Their rare-gas geochemistry indicates that the upper and lower mantle are compositionally and isotopically distinguished reservoirs(Hilton and Porcelli 2014). For example, the He contents and isotopic ratios(3He/4He)in MORBs differ from those in OIBs (Graham 2002; Moreira and Sarda 2000).

MORBs unaffected by a mantle plume (OIBs) typically display a narrow range of3He/4He ratios,7-9RA,where RAis the atmospheric3He/4He ratio (1.4 × 10-6) (Graham 2002).By contrast,many OIBs have higher3He/4He ratios than MORBs (Graham 2002), with the highest ratios of 50 RAfound at Baffin Island (Stuart et al. 2003). These high3He/4He OIBs are associated with high143Nd/144Nd, indicating the depleted nature relative to a chondritic bulk silicate Earth value(Class and Goldstein 2005).Also,these OIBs often have high hotspot buoyancy fluxes indicating their source material was entrained from the deep mantle only by the hottest, most buoyant plumes (Jackson et al.2017),and the negative tungsten isotope anomalies in these OIBs indicate that they are derived from the materials in the core–mantle boundary (Jones et al. 2019). The undegassed and primordial lower mantle is the common explanation for high3He/4He ratios found in OIBs(Alle`gre et al.1983;Kurz et al.1982).The OIBs with high3He/4He ratios such as the basalts in Loihi–Kilauea tend to show several orders of magnitude lower helium concentrations than MORBs (Moreira and Sarda 2000), however. This apparent discrepancy is the so-called helium concentration paradox, proposed by Anderson (1998). This problem is still open although many models have been proposed(Moreira 2013).

The decay of238U,235U, and232Th in the mantle produces not only4He but also heat in constant proportions.We can expect a fixed ratio of heat and4He released at the Earth’s surface since heat and4He are synchronously created.However,the observed He released is almost an order of magnitude less than what would be expected. This apparent imbalance is the heat–helium paradox (Onions and Oxburgh 1983). The transition zone at the top of the lower mantle had been speculated as the boundary layer through which heat could pass but not He (Onions and Oxburgh 1983; Oxburgh and Onions 1987). This explanation has not been tested or proved by experiments,so the heat and helium imbalance is still a robust issue (Tucker et al. 2018; van Keken et al. 2001).

3 Numerical experiments

To evaluate whether the Soret effect of helium is working in the mantle,we performed simple numerical experiments to solve diffusion equation using finite difference method.The settings of the numerical experiments are the followings: initial equilibrated concentration gradient is about 1 cm-1(dashed black lines in Fig. 1), which can be assumed to be caused by temperature gradient. The initial conditions are set by changing positions of two neighboring cells without changing their concentrations (blue lines in Fig. 1),i.e.,the two black dots’positions are transposed to each other,and their compositions are corresponding to the horizontal blue dots’ (Fig. 1). Also, this interchange of positions can be assumed to be produced by convection.As time elapsed, the system will tend to be ‘re-homogenized’by diffusion(red lines in Fig. 1),i.e.,red lines originally at the positions of the blue lines will gradually move to the positions of the dashed black lines.Following the criterion that the system is re-equilibrated when difference of instant and equilibrated concentration is less than 1/10 of the difference of initial and equilibrated concentration (Kellogg and Turcotte 1987), i.e., (Creddot- Cblackdot)/(Cbluedot- Cblackdot) ≤0.1, we get times required for equilibration are 0.32 years for D = 10-11m2/s (Fig. 1a)and 0.033 years for D = 10-10m2/s (Fig. 1b). The related animations are present in supplementary information.

The typical convective velocity of the upper mantle is 20 cm/year (Weismueller et al. 2015), i.e., it takes 0.05 years to vertically move 1 cm by convection in the upper mantle. Note it is not necessary to take horizontal moving of mantle convection into account, because we only consider the vertical moving of mantle convection which produces the adiabatic temperature gradient.According to our numerical results, it will take 0.32 years to erase the compositional shift (Fig. 1a). Therefore, we can safely say that convection in the upper mantle can effectively homogenize these components with their diffusivities less than 10-11m2/s. Whereas the typical convective velocity of the lower mantle is 1.5 cm/year(Butterworth et al.2014),it takes 0.67 years to move 1 cm in the lower mantle.Hence,convection in the lower mantle can’t wipe away the compositional zonation by these components with their diffusivities larger than 10-11m2/s(Fig. 1a).

4 Theoretical model

No laboratory experiments have investigated helium elemental and isotopic fractionations by Soret effect but important insights can be obtained based on theoretical considerations. Below, we set a model and evaluate how thermal diffusion processes could have made helium elemental and isotopic fractionation in mantle rocks.

The model settings are the followings: a 100-cm long mantle peridotite bar is put in a closed system at pressure 7 Gpa and temperature 1400 °C.The initial He content and isotope in the peridotite bar are homogeneous and4He and3He concentrations are 9.5 × 10-10and 1.2 × 10-14(ccSTP/g)respectively,so the3He/4He ratio is 9 RA.Now a temperature gradient is imposed with the top end of the peridotite bar at 1200 °C and the bottom end at 1600 °C(Fig. 2a).At a finite timescale(e.g.,200 years),we analyze the distributions of elements and isotopes of He in the peridotite bar. We only consider the helium’s diffusion because the diffusion of major components in mantle minerals is over four orders of magnitude less than that of He (Chakraborty 2010; Cherniak and Watson 2012). For example, the characteristic diffusion distance of Mg in olivine is less than 1 cm in 200 years;while for helium it is over 25 cm based on diffusivity data from Cherniak and Watson(2012)and Chakraborty(2010).In other words,we can approximate that the chemical environments are similar in the cold and hot end of the peridotite bar within a finite time-scale. The He fugacity (fHe), i.e., He activity, is only a function of temperature.

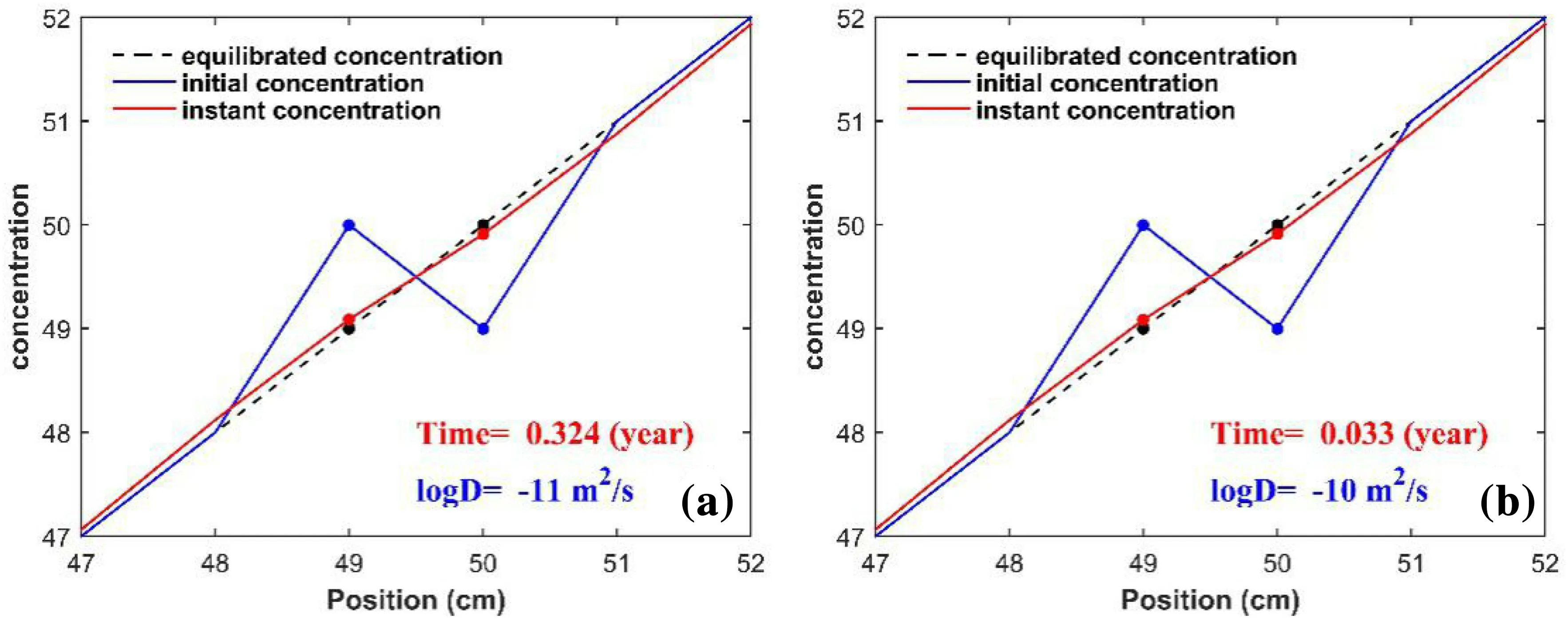
Fig. 1 Time required for diffusion equilibrium. a For diffusion coefficient (D) = 1 × 10-11 m2/s, b for diffusion coefficient (D) = 1 × 10-10 m2/s. The settings of initial and boundary conditions are detailed in the main text, and related animations are present in supplementary information

Since helium’s experimental data in mantle minerals are sparse(Jackson et al.2013;Parman et al.2005),we simply assume that fHeincreases tenfold by every 100 °C of increase in temperature based on the functional relationship of fO2-T(O’Neill and Wall 1987).It is possible that helium obeys Henry’s law at low fHeconditions due to its inert property (Jackson et al. 2013), hence we also assume fHe–CHe(CHeis helium concentration) follows a positive proportional relationship:

where KHis the Henry’s constant. At initial stage (homogenous system),the fHein the hot end(fHehot)is 104times that in the cold end,then helium in the hot end is diffusing toward to the cold end of the peridotite bar to decrease the difference of chemical potential (fHe) of the two ends according to Zhang(1993).According to Eq. (1),it can be expected that the He concentration in the cold end(CHecold)is 104times that in the hot end (CHehot) when equilibrium is reached ((Fig. 2a).

If we define δ4Heair= 0‰, then δ4Hesample= ([4He/3-He]sample/[4He/3He]air- 1) × 1000, where [4He/3He]air-= 7.14 × 105.δ4Hecoldand δ4Hehotare δ4He values in the cold and hot end of the peridotite bar,respectively.Thotand Tcoldare temperatures in K in the cold and hot end,respectively. Based on the theoretical model of isotope fractionation by thermal diffusion (Li and Liu 2015):

The calculated δ4Hecoldis 104‰ higher than the δ4Hehot(Fig. 2b).If we set the cold end3He/4He ratio is 8 RA,then the calculated hot end3He/4He ratio is 47RA. The calculated3He/4He ratios and [3He] in the peridotite bar are present in Fig. 2c, d.

5 Application: a helium stratified and ingassed lower mantle

Although much is unknown in the low mantle,our model can be applied to solving the He concentration paradox in the mantle based on its inert nature. The [4He] and [3He] in undegassed MORBs are estimated to be 4.0 × 10-5and 4.4 × 10-10ccSTP/g,respectively(Tucker et al.2018),then their estimated abundances in the upper mantle are 4.0 × 10-9and 4.4 × 10-14ccSTP/g respectively,based on the partition coefficients(KHe～10-4)between upper mantle minerals and melt (Jackson et al. 2013). Given the temperature difference between the bottom and top of the lower mantle is 400 °C,the calculated He abundances and isotope compositions in the bottom of the lower mantle are: [4-He] = 4.0 × 10-13ccSTP/g, [3He] = 2.6 × 10-17ccSTP/g and3He/4He = 47 RA. Therefore, the calculated [4He] and3He/4He in undegassed OIBs are 4.0 × 10-9ccSTP/g and 47 RA,respectively,given the KHe= 10-4(Jackson et al.2013).Fractionations of[4H]and3He/4He in MORBs and OIBs are shown in Fig. 3.Our Soret effect model readily explains the elemental and isotopic fractionations of helium in MORBs and OIBs.Most[4H]data in MORBs is lower than the model predicted; while most [4H] data in OIBs is higher than the model predicted (Fig. 3). We attribute the MORBs’ case to degassing (Gonnermann and Mukhopadhyay 2007; Tucker et al. 2018), and the OIBs’ case to ingassing (the reason is discussed below).

The reason for homogenous helium isotope in MORBs is due to the vigorous convection in the upper mantle, and the sluggish convection in the lower mantle leads the adiabatic temperature gradient to take effect. This elemental and isotopic effects caused by Soret effect create a helium stratified lower mantle, i.e., the lowermost mantle has highest3He/4He ratios and lowest He content,which is the so-called He concentration paradox (Anderson 1998). The helium stratified lower mantle is consistent with OIBs from Iceland, Hawaii, Samoa and Pitcairn exhibiting not only negative μ182W values (Mundl et al. 2017), but also the highest3He/4He ratios (Jackson et al. 2017; Mundl et al.2017), because the lowermost mantle have more chance to incorporate core materials which have large negative μ182W values (Kleine et al. 2002). Moreover, faster upwelling rate of mantle plume, which is positively correlated with flux buoyancy (White 2010), usually has highest maximum3He/4He ratios (Jackson et al. 2017),indicating the deepest mantle signature of high3He/4He ratios can survive in the rising process.

The adiabatic temperature gradient is created by mantle convection,so it is an intrinsic feature of the mantle.In the above, we only show that the adiabatic temperature gradient can hold the elemental and isotopic effects of helium in the present lower mantle (Fig. 1a), and we don’t know when the helium stratified lower mantle was formed?Following the analysis results of Kellogg and Turcotte(1987), the time required to form the helium stratified lower mantle is:

where this time, a is the vertical size of the lower mantle(2240 km) and D is diffusion coefficient of He. ε is strain rate and it is equal to mantle convection velocity (ν)divided by a.At the conditions of the present lower mantle,i.e., D = 1×10-10m2/s, ε = 1.5 cm year-1/2240 km = 2×10-16s-1, the calculated this 1.5 Gyr.Considering convection is probably more vigorous in the lower mantle of early Earth than the present,this probably less than 150 Ma, given D = 1×10-9m2/s and ε = 2×10-15s-1. This assertion is consistent with high3He/4He OIBs are often accompanying with high143Nd/144Nd demonstrating a depleted nature (Class and Goldstein 2005), because this depleted nature is probably associated with early continental crust formation (Kemp and Hawkesworth 2014), and the combined He-, Pb- and Nd-isotopic compositions in Baffin Island lavas suggest that their source was formed between 4.55–4.45 Gyr(Jackson et al. 2010).

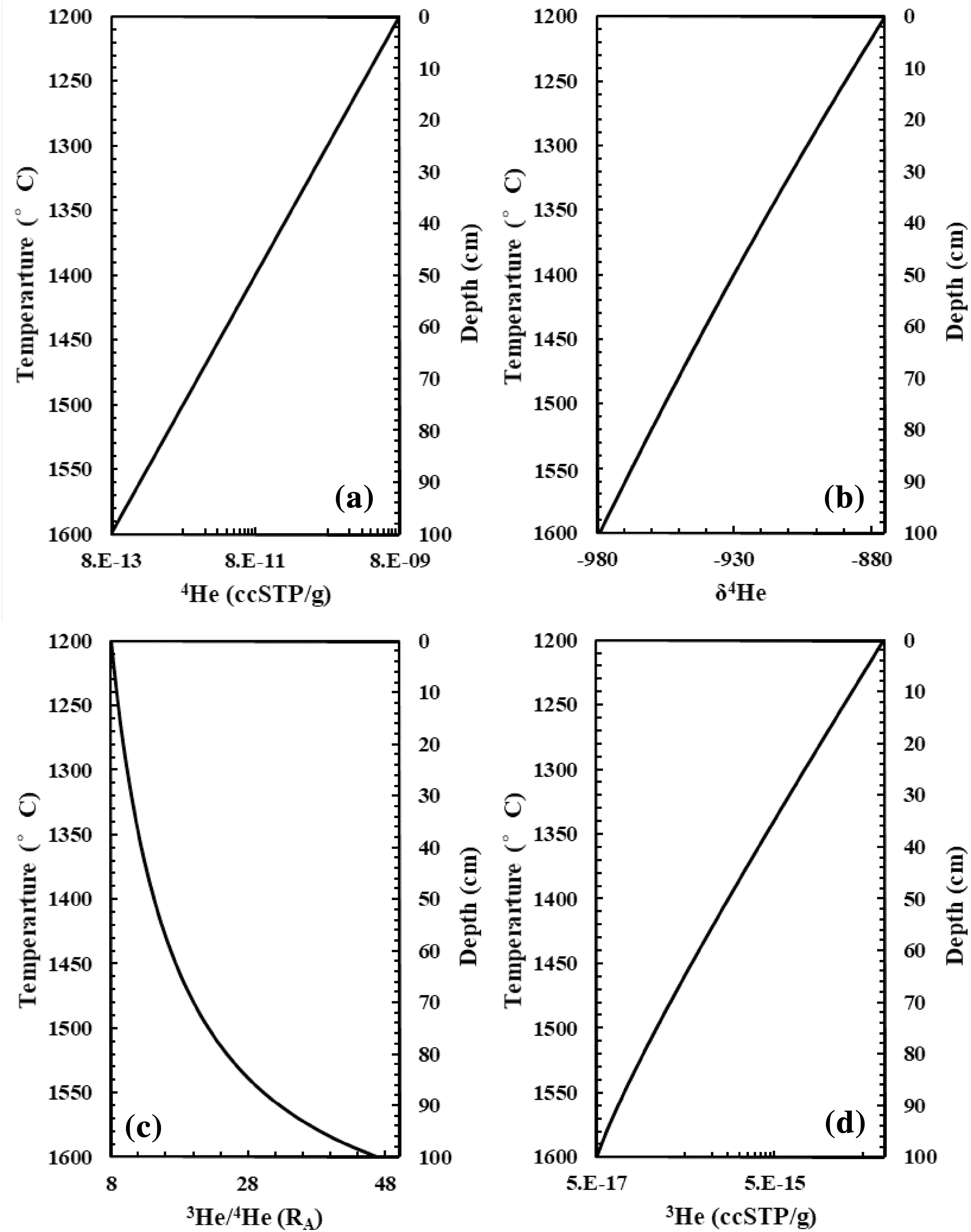
Fig. 2 Elemental and isotopic fractionations of helium by Soret effect. a T versus 4He,b T versus δ4He, c T versus 3He/4He, d T versus 3He

The initial3He/4He isotopic ratios of the Earth, i.e., the initial He isotopic ratio in our solar system, is believed to be equal to that of Jupiter (120 RA) (Mahaffy et al. 1998).According to our model and helium evolution of the Earth(Porcelli and Elliott 2008), the predicted initial3He/4He ratios in the deepest lower mantle of early Earth was over 150 RA,higher than the initial He isotopic ratio in our solar system, if helium stratified lower mantle was formed in 100 Ma after the Earth was formed. Because the temperature contrast across the lower mantle in the early Earth is the largest.

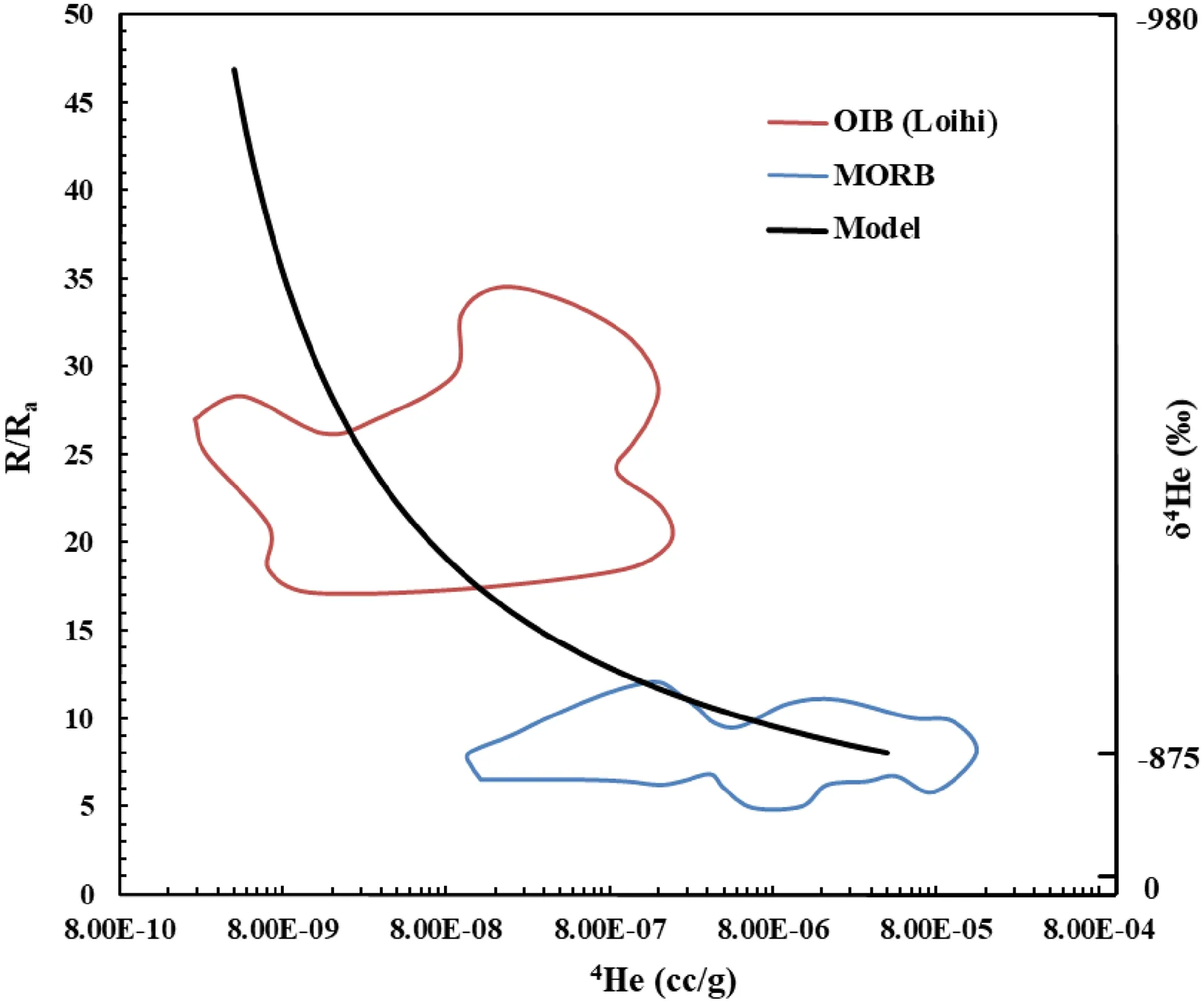
Fig. 3 Fractionations of [4H] and 3He/4He in MORBs and OIBs.Fields of MORBs and OIBs are from Moreira and Sarda (2000).Definition of δ4He and related calculations are described in the main text

In the early Earth,He stratified lower mantle was likely formed under a large temperature gradient due to a hotter mantle than the present.In other words,that the largest fHedifference between the top and bottom of the lower mantle,would result in the lowest helium contents in the early lowermost mantle in the whole history of the Earth. The secular cooling of the interior mantle would decrease fHecontrast of the top and bottom of the lower mantle. This means that the He contents in the lower part of the lower mantle have been increasing during the evolution (secular cooling) of the Earth. For example, we fix the [4He] concentration and temperature in the top of the peridotite bar in Fig. 1a, then, we calculate [4He] concentration by just decreasing the bottom temperature by 100 °C. The [4He]concentration distributions by Soret effect of different temperature (ΔT) contrast are present in Fig. 4. The total[4He]of ΔT = 300 is 30%higher than that of ΔT = 400 °C Fig. 4. Therefore, the evolution of the lower mantle is a helium ingassed process, as the surface temperature of the Earth is nearly changeless (Wilde et al. 2001), and 300–400 °C cooling of the interior of Earth since 4.4 Gyr to the present. Some radiogenic He produced by the decay of U and Th would be trapped by the lower mantle; while the accompanying heat had been released away. This maybe is the solution for the apparent imbalance of heat and helium,the heat–helium paradox(Onions and Oxburgh 1983).

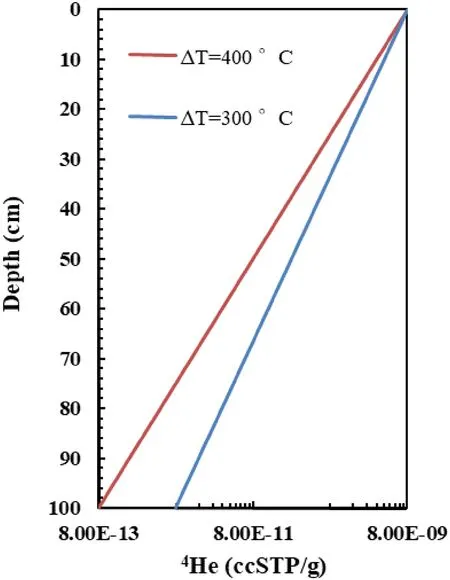
Fig. 4 Helium separations by Soret effect in different temperature contrast

Besides He,H and Li are also fast-diffusion components in the solid mantle(Demouchy and Bolfan-Casanova 2016;Dohmen et al. 2010; Hae et al. 2006; Sun et al. 2015).Elemental and isotopic effects by thermal diffusion may play a role to shape their behaviors in the mantle.However,it is impossible to evaluate the effect in H and Li at present because they are chemically active rather than inert and litter is known in the lower mantle. Further experimental and theoretical calculation works are needed to define their behaviors in the lower mantle, such as the fugacity or activity.

AcknowledgementsWe thank Dr.Huiming Bao,Yun Liu,Qingwen Zhang, Xiaobin Cao and Chunhui Li for their constructive discussions. Funding for this study comes from the Strategic Priority Research Program(B)of CAS(XDB18010100)and the Chinese NSF projects (41490635, 41530210, 41225012, 41573040).