内外键槽尺寸链的分析与计算

2020-04-24中车戚墅堰机车车辆工艺研究所有限公司江苏常州213011蒋永建

金属加工(冷加工) 2020年3期

■ 中车戚墅堰机车车辆工艺研究所有限公司（江苏常州 213011）蒋永建

1. 问题的提出

在设计机械零部件各要素的几何精度时，往往要通过综合分析计算，来协调和保证零部件的整体精度要求，合理规定各要素的尺寸精度和形位精度。对几何精度的综合分析计算，通常运用尺寸链理论来解决。

机械设计包括结构设计、参数设计以及尺寸链计算（公差设计）等方面，但产品质量差、

性能价格比低以及交货周期长等也直接反映出产品制造精度或配合精度的低下。熟悉尺寸链理论知识能比较合理地、经济地和高效地分配各个零件的制造、装配公差，真正实现产品的高质量、低成本和大批量生产。在生产过程或成品检验中，经常碰到产品内外键槽的几何参数超差问题，所以公差的合理分配显得尤为重要，尤其对内外键槽的线切割加工和磨削具有重要意义。

2. 原因分析

尺寸链具有两个特性：封闭性和关联性。相互关联尺寸相互影响，制约着产品装配精度和尺寸精度，特别是工序安排也影响最终尺寸精度。几何公差小、精度要求高，必然使加工公差范围缩小，增加加工难度，故公差分配更要精确。诸如带键槽的内孔、外圆产品结构，若先精磨再安排线切割键槽，必然使线切割对刀及形位精度影响到产品的最终质量，故而半精车后先安排粗磨、线切割，再安排精磨，可更有效地保证质量，且工序比较合理。要求设计人员准确运用尺寸链的公差设计，合理、经济分配公差，从而满足产品质量要求；要求操作工和检验人员能及时发现不合理的地方进行改善，防止批量问题出现并流转至下一工序，应及时反馈过程问题，加强过程质量成本控制。

诸多质量问题的产生，很大程度上是因为没有掌握尺寸链设计计算知识，操作者或检验人员没有及时发现问题并反馈过程问题以及调整加工公差等。

3. 分析与计算

在产品设计时，除了需要进行运动、强度和刚度等计算外，还需进行几何量分析计算（即精度设计），以确定零件的尺寸公差、几何公差等。其目的在于保证设备能顺利进行装配，并能满足预定的功能要求。

加工过程中，由于有许多工序，一方面由于加工需要，在工序图及工艺卡片上要标注一些专供加工使用的工艺尺寸，工艺尺寸往往不是直接采用零件图上的尺寸，而是需要另行计算；另一方面，当零件加工时，有时需多次转换基准而引起工序基准、定位基准或测量基准与设计基准不重合。这时，需要利用工艺尺寸链原理来进行工序尺寸及其公差的计算。

经常会遇到以下三种情况的内外键槽计算，需要通过核算尺寸链来规避质量风险、检验合格公差控制范围，保证产品加工精度。

4. 工件内孔键槽分析计算

如图1所示，内孔D1为φ85+0.035+0m m，键槽尺寸深度为90.4+0.20+0mm。内孔及键槽的加工顺序为：①精镗孔至D2为

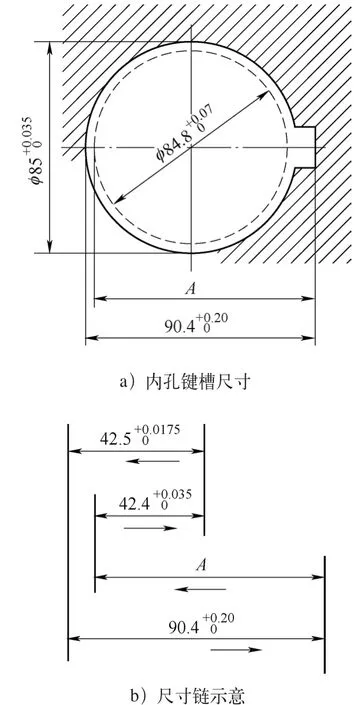
图1 工件内孔键槽

φ84.8+0.07mm。②插键槽至尺寸A

（通过工艺计算确定）。③磨内孔至φ85+0.035mm，同时间接保证

键槽深度90.4+0.20mm的要求。求

+0尺寸A。

求解过程如下。

（1）列尺寸链列尺寸链如图1b所示。

（2）判断各环根据题意，判定封闭环为键深90.4+0.20mm，

+0增环为A、，减

（3）计算 A＝90.4-42.5＋42.4=90.3（mm）。因为+0.2＝+0.0175＋ESA-0，所以上偏差ESA＝+0.182 5（mm）；因为0＝0＋EIA-0.035，所以下偏差EIA＝+0.0 3 5（m m）。故A＝90.3+0.1825+0.0350mm。

分析：在过程加工中完成键槽线切割，保证最终质量满足要求，节约成本，提高效率。

5. 工件外圆键槽分析计算

如图2所示，要求在轴上铣一

图2 工件外圆键槽

求解过程如下。

（1）画尺寸链图尺寸链如图2b所示。

（2）判断各环 A0＝N＝是封闭环；R＝A/2＝33A是增环；R＝21是减环。

（3）计算 A2＝N-A3/2＋A1/2＝62-35＋35.25＝62.25（mm）。因为0＝ESA2＋ESA3/2-EIA1/2＝ESA2＋0-（-0.05），所以上偏差ESA2＝-0.05mm；因为-0.3＝EIA2＋EIA3/2-ESA1/2＝EIA2-0.03-0，所以下偏差EIA2＝-0.27m m。故键槽尺寸A2＝62.25-0.05-0.27mm。

分析：精磨外圆前按设计的公差要求完成线切割，有效规避了加工错误、磕碰及工装装夹等质量风险。