车轮荷载作用下双工字钢组合梁桥横桥向焊钉拉拔效应

刘永健，吴浩伟，封博文，张泽军，陆力伟

(长安大学 公路学院，陕西 西安 710064)

0 引 言

双工字钢组合梁桥具有工业化程度高、质量可控性强、构造简单、经济性高、施工高效等诸多优点[1-2]，在法国等欧洲国家已有较多实践，2016年中国在安徽济祁高速公路淮河桥对这种桥型进行了首次应用[3]。

相比于多主梁，双工字钢组合梁桥的主梁间距大，桥面板悬臂长度长，在车轮荷载作用下，组合梁横向弯曲效应明显，在钢梁上翼缘跟随桥面板变形受到约束时，组合梁界面会发生横桥向掀起现象，焊钉产生较大的拉拔应力。在车轮的反复加载下，焊钉处于周期性剪拔共同作用的复杂应力状态，降低焊钉使用寿命，影响组合梁桥使用年限[4-6]。现行的《公路钢结构桥梁设计规范》(JTG D64—2015)[7]规定，当相邻主梁间距较大时，钢混界面可能会有较大的拉拔力，应在连接件设计时给予重视。因此，有必要对车轮荷载作用下，双工字钢组合梁桥由于钢混界面横桥向掀起引起的焊钉拉拔应力分布规律及影响因素进行研究。

现有文献集中在组合箱梁桥的焊钉横桥向拉拔效应研究。张俊平等[8]进行了大悬臂钢混结合梁节段模型试验，对钢混组合箱梁焊钉拉拔力大小与分布规律进行研究；邵长宇[9]以上海长江大桥为工程背景，基于局部模型试验与有限元数值模拟方法对均布式焊钉组合箱梁的拉拔力进行研究，发现当焊钉布置位置接近腹板加劲肋时，横向掀起位移大幅减小，反之则大幅增加，但腹板加劲肋附近焊钉将承受较大的拉拔力，建议焊钉布置应兼顾掀起位移与焊钉拉拔力；侯健等[10]采用有限元数值模拟方法，对集束式焊钉组合箱梁在恒载和汽车偏载作用下钢混界面的横桥向掀起现象进行分析，认为采用集束式焊钉布置能有效防止组合梁钢混界面横桥向掀起现象，钢混界面的横桥向掀起位移十分小；周辉[11]基于ANASYS软件，对偏心荷载作用下简支与连续组合钢箱梁界面滑移效应与掀起效应的关系进行了研究，认为滑移效应与掀起效应相互影响。双工字钢组合梁属于开口截面，扭转刚度较小，在荷载作用位置横梁布置方式会对钢梁侧向变形产生影响，进而影响焊钉拉拔应力，组合箱梁的研究成果不能完全解决双工字钢组合梁焊钉拉拔效应的问题。

为此，本文采用有限元软件，以2×35 m连续双工字钢组合梁为研究对象，对不同荷载作用位置、加劲肋与横梁布置方式时焊钉拉拔应力的分布规律进行研究，并对桥面板厚度与主梁间距比、横梁位置、焊钉间距对焊钉拉拔应力的影响以及各参数敏感性进行分析。

1 计算模型与分析方法

1.1 模型设计

2×35 m连续双工字钢组合梁桥布置如图1，2所示。桥梁全长70 m，计算跨径34.07 m。各部件尺寸及材料如表1所示。

组合梁主梁高2.2 m，钢梁的梁高H为1.8 m，间距L为6.7 m，桥面板宽12.75 m，钢梁之间桥面板厚度h为270 mm。支座附近10.5 m范围加劲肋间距为1.75 m，跨中14 m范围内加劲肋间距为3.5 m，横梁间距为3.5 m。A-A截面主梁间设置1道工字形小横梁，横梁中心线距钢梁上翼缘距离Z为800 mm，钢梁内侧设置T型加劲肋，外侧无加劲肋。桥面板与钢梁采用集束式焊钉相连，焊钉长200 mm，直径为25 mm，剪力槽中心间距为1.125 m，荷载作用位置剪力槽内的B处焊钉布置如图3所示。原设计中焊钉横桥向间距dj为120 mm。

加劲肋限制了钢梁翼缘跟随桥面板变形，导致焊钉产生拉拔应力。横梁的设置限制了钢梁侧向变形，一定程度上限制了钢梁翼缘跟随桥面板变形，对焊钉拉拔应力产生较大影响，同时焊钉拉拔应力沿横桥向分布还受到荷载作用位置影响。根据横梁与加劲肋设置情况以及车轮荷载沿横桥向布置位置分为12个工况，对焊钉拉拔应力的大小及分布进行研究，工况具体加载与构造如表2所示。车轮荷载大小(1个后车轮轴重)按《公路桥涵设计通用规范》(JTG D60—2015)[12]确定，每个车轮荷载大小70kN。车轮荷载沿纵桥向作用于A-A截面，荷载作用位置如图1所示；横桥向车轮荷载按梁间荷载PZ和悬臂端荷载PX两种方式布置，梁间荷载PZ横向布置位置是将双工字钢组合梁桥面板简化为简支梁后，根据简支梁弯矩影响线的最不利位置确定，悬臂端荷载PX横向位置是按《公路桥涵设计通用规范》(JTG D60—2015)所容许的车轮距桥面板自由端最近距离确定，具体布置如图2所示。

图1 双工字钢组合梁立面布置(单位：mm)

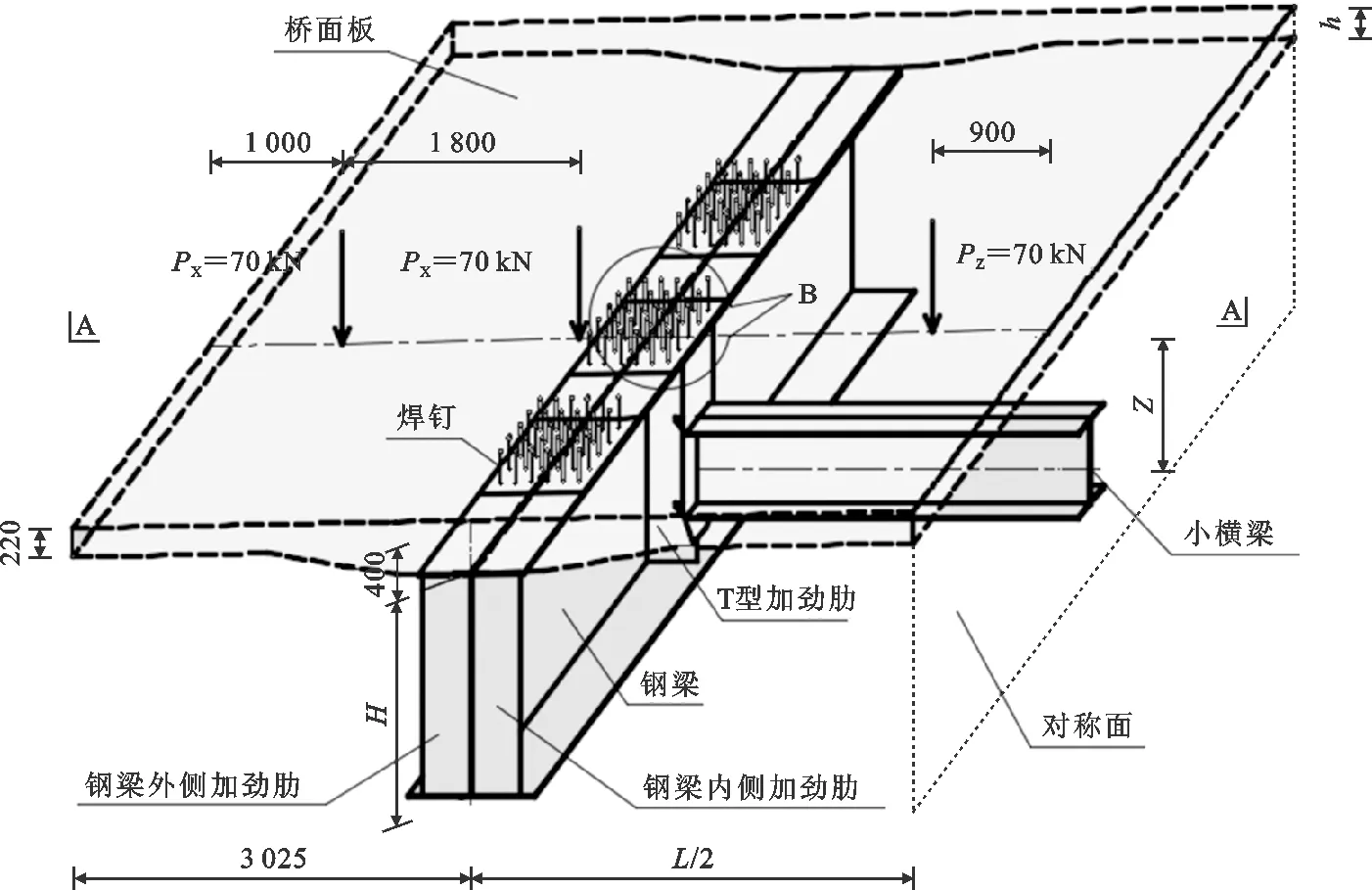
图2 双工字钢组合梁尺寸及荷载布置(单位：mm)

表1 组合梁各部件尺寸及材料

注：以纵桥向为行，横桥向为列，编号时先行后列，如51号焊钉表示第5行第1列焊钉；负值代表焊钉受压。

焊钉拉拔应力由于桥面板横向弯曲产生，主梁间桥面板厚度h与钢主梁间距L的比值对桥面板横向弯曲有较大的影响，将主梁间桥面板厚度h与钢主梁间距L的比值定义为参数k1。分析最不利工况下k1对焊钉拉拔应力的影响，k1研究范围为0.03～0.07。

横梁位置的改变对其限制双工字钢组合梁侧向变形产生影响，钢梁翼缘跟随桥面板变形随之发生变化，进而对焊钉拉拔应力产生影响，因此以横梁中心线距钢梁上翼缘顶面距离Z与钢梁高度H的比值k2为研究参数，分析最不利工况下横梁设置位置对焊钉拉拔应力的影响，k2取值如表3所示。

焊钉拉拔应力还与横桥向间距dj有关，根据现行的《公路钢结构桥梁设计规范》(JTG D64—2015)确定焊钉横向间距为70～110 mm，研究最不利工况下焊钉横桥向间距变化对焊钉拉拔应力的影响。

1.2 分析方法

选用文献[9]组合梁桥焊钉拉拔效应试验中试件ML-1，在70 kN荷载下钢混界面掀起位移沿纵横桥向的分布及由拉拔力引起的焊钉最大轴向应变，对不同模拟方式进行对比验证。本文研究组合梁在弹性受力范围内的焊钉拉拔效应，因此材料只考虑其弹性力学性能，钢材Q345弹性模量为2.06×105MPa，泊松比为0.31；桥面板C60混凝土材料弹性模量为3.60×104MPa，泊松比为0.2。基于ABAQUS的有限元试验模型如图4所示。对比了6种不同的组合梁模拟方式，各方法的单元选取、焊钉模拟方式、桥面板与钢梁界面模拟以及焊钉与混凝土桥面板接触关系如表4所示，其中桥面板与钢梁的库仑摩擦因子取0.3[13-18]。

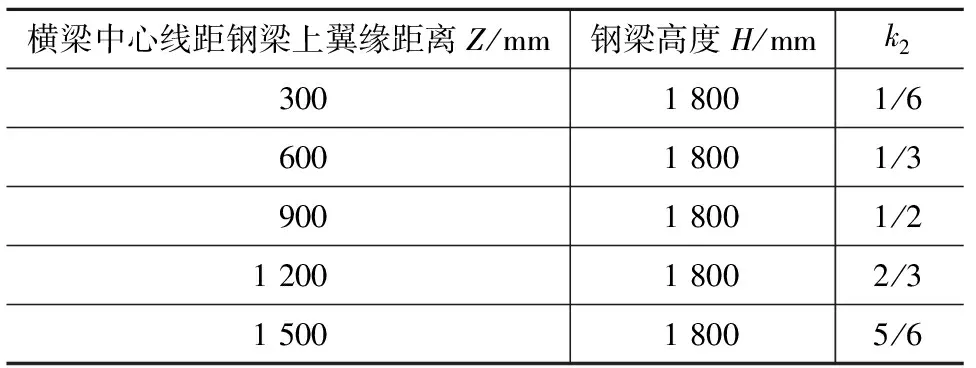
表3 横梁位置与对应的k2

图4 试件ML-1有限元模型

当焊钉采用弹簧单元模拟[19-20]时，设置纵横桥向的切向刚度及轴向刚度。按《公路钢混组合梁桥设计与施工规范》(JTG/T D64-01—2015)[14]计算抗剪刚度，即

(1)

式中：kss为焊钉的抗剪刚度；dss为焊钉杆部直径；Ec为混凝土弹性模量；fck为混凝土抗压强度标准值。

轴向刚度Kv按轴心受拉理论公式(2)计算[21]

Kv=EstAst/l

(2)

式中：Kv为焊钉轴向刚度；Est为焊钉弹性模量；Ast为焊钉的截面面积；l为焊钉的长度。

当焊钉采用实体单元时，焊钉与钢梁采用绑定(Tie)接触，焊钉与桥面板的接触关系分2类，一类是在桥面板内开出焊钉形状[22-24]，焊钉与桥面板间采用硬接触，模拟受压时焊钉与混凝土桥面板接触却不穿透，同时焊钉与桥面板间设置罚函数，摩擦因数取0.3，模拟焊钉与混凝土之间的摩擦；另一类是将焊钉内置(Embedded Region)到桥面板中。

有限元计算得到的横桥向掀起位移沿纵桥向和横桥向的分布与文献[9]实测结果对比如图5所示。模拟方式5与模拟方式6有限元曲线与试验曲线基本吻合；对比由于界面横桥向掀起引起的焊钉最大轴向应变，文献中的试验值为1 685×10-6，模拟方式5计算得到的焊钉最大轴向应变为1 541×10-6，与试验值相对误差为8.55%；模拟方式6计算得到的焊钉最大轴向应变为1 346×10-6，与试验值相对误差为20.12%。综合计算精度与计算效率，推荐采用模拟方式5模拟双工字钢组合梁有限元模型。

图5 有限元结果与文献[9]实测结果对比

图6 双工字钢组合梁有限元模型

2×35 m连续双工字钢组合梁模型如图6所示，为简化模型计算量，根据文献[9]中集束式焊钉组合箱梁界面横桥向掀起效应沿纵桥向的分布范围约为0.3 m的结论，对荷载作用点和作用点左右相邻的剪力槽内的焊钉采用实体单元模拟，其余剪力槽内的焊钉选用弹簧单元模拟。

双工字钢组合梁钢材Q345的弹性模量为2.06×105MPa，泊松比为0.31；桥面板C50混凝土的弹性模量为3.45×104MPa，泊松比为0.2。考虑钢筋对分壳单元；S4为4节点四边形有限薄膜应变线性完全积分壳单元。

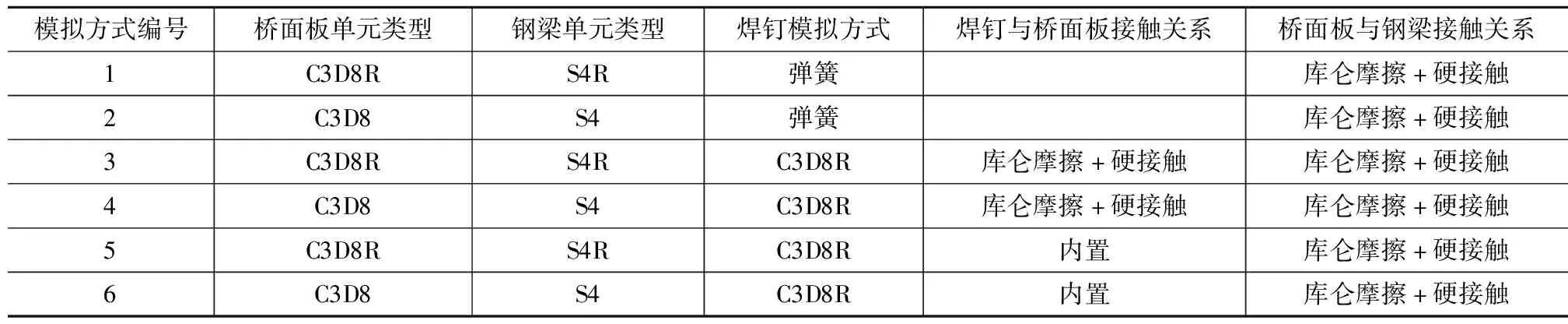
表4 焊钉与界面模拟方式

注：C3D8R为8节点六面体线性减缩积分单元；C3D8为8节点六面体线性完全积分单元；S4R为4节点四边形有限薄膜应变线性减缩积桥面板刚度的贡献，组合梁模型中桥面板钢筋采用T3D2单元进行模拟，钢筋弹性模量取2.0×105MPa，泊松比取0.3，钢筋内置(Embedded Region)于混凝土桥面板内。

2 焊钉拉拔应力沿纵桥和横桥向分布规律

2.1 焊钉拉拔应力沿横桥向分布规律

2.1.1 加劲肋设置的影响

组合梁焊钉拉拔应力T沿横桥向分布如图7所示。当车轮荷载作用位置钢梁内外侧均无加劲肋(工况L-1和工况X-1)时，焊钉无明显拉拔应力，而其余设置加劲肋的荷载工况，只有在上翼缘下方设置加劲肋的焊钉出现轴向应力，说明只有当焊钉所在的钢梁上翼缘随桥面板变形受到加劲肋限制时，焊钉才会出现轴向应力。

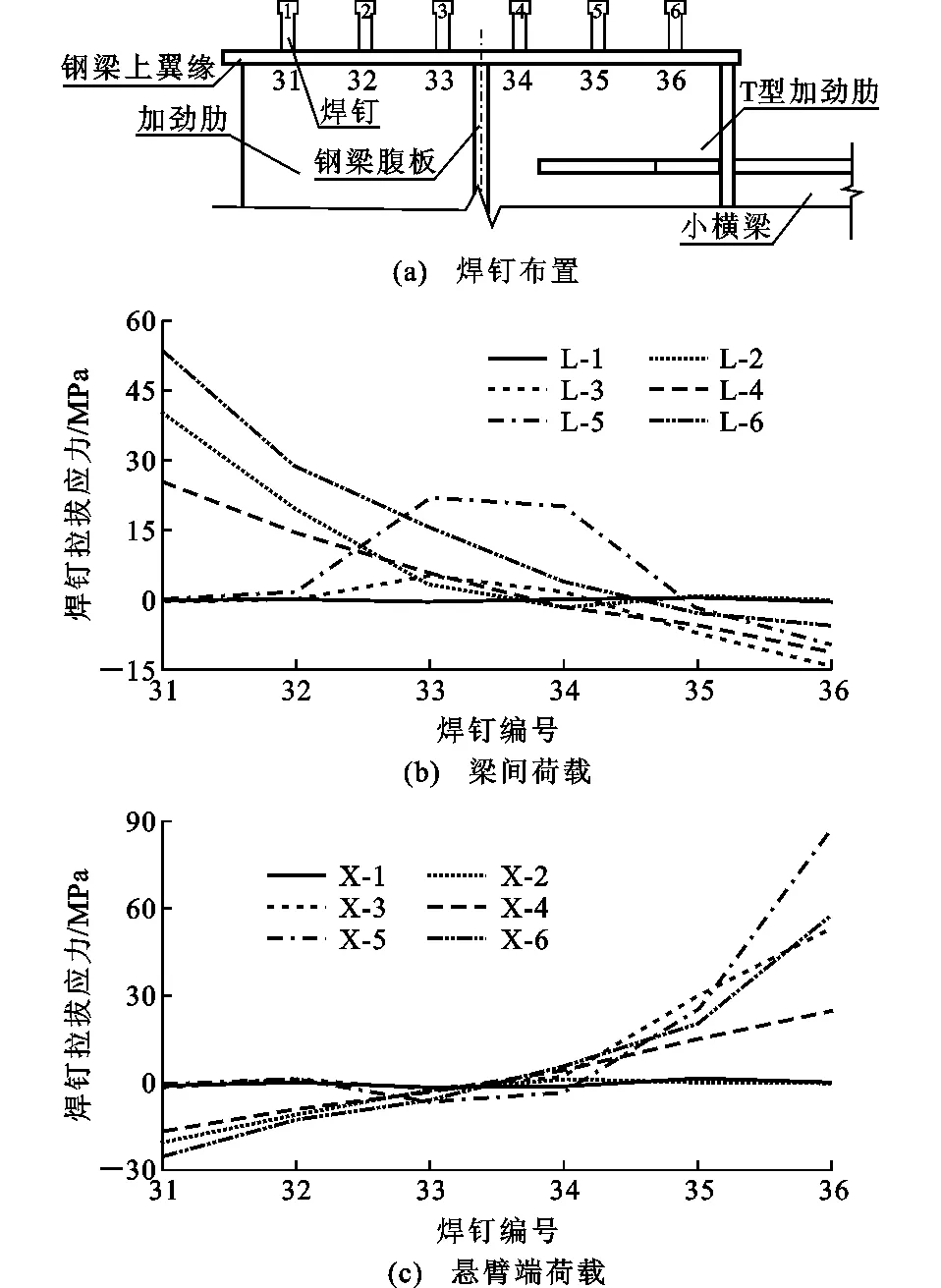
图7 T沿横桥向分布

若车轮荷载作用位置钢梁内外侧只设置1片加劲肋，则焊钉拉拔应力沿横桥向分布和数值因荷载作用位置与加劲肋设置位置的不同而不同。梁间荷载作用下，只在外侧设置加劲肋钢梁(工况L-2)的焊钉拉拔应力峰值出现在钢梁外侧翼缘附近；只在钢梁内侧设置加劲肋(工况L-3)的焊钉拉拔应力峰值出现在钢梁腹板位置，由于只在内侧设置加劲肋焊钉拉拔力力臂小于在外侧设置加劲肋焊钉拉拔力力臂，因此在梁间荷载作用下内侧设置加劲肋(工况L-3)的焊钉拉拔应力小于外侧设置加劲肋(工况L-2)的焊钉拉拔应力，如表2所示。悬臂端荷载作用下，车轮荷载位于钢梁外侧上翼缘位置，当只在钢梁外侧设加劲肋(工况X-2)时，所有焊钉处于受压状态，最大焊钉压应力峰值出现在钢梁上翼缘外侧位置；当只在钢梁内侧设置加劲肋时(工况X-3)，焊钉出现拉拔应力，焊钉拉拔应力峰值出现在钢梁上翼缘内侧。

车轮荷载作用位置钢梁内外侧均设置加劲肋(工况L-4和工况X-4)时，焊钉拉拔应力沿横桥向近似线性分布。内外侧均设置加劲肋焊钉拉拔应力(工况L-4和工况X-4)峰值出现位置与只在远离荷载作用翼缘下方设置加劲肋的焊钉拉拔应力(工况L-2和工况X-3)峰值出现位置相同。荷载作用位置下方无加劲肋支承时，桥面板变形更明显，只在远离荷载作用翼缘下方设置加劲肋的焊钉拉拔应力(工况L-2和工况X-3)峰值大于内外侧均设置加劲肋的焊钉拉拔应力(工况L-4和工况X-4)峰值。

2.1.2 横梁设置的影响

从图7组合梁焊钉拉拔应力T沿横桥向分布可以看出，荷载作用位置有无横梁对拉拔应力沿横桥向分布无明显影响，但横梁的设置使组合梁焊钉拉拔应力大幅增加。从表2中焊钉最大拉拔应力对比中可以发现：工况L-5的焊钉最大拉拔应力比工况L-3大317.97%，工况L-6的焊钉最大拉拔应力比工况L-4大112.08%；工况X-5的焊钉最大拉拔应力比工况X-3大64.15%，工况X-6的焊钉最大拉拔应力比工况X-4大137%，说明在同样的荷载布置与加劲肋设置条件下，荷载作用位置设置横梁提高了钢梁的抗扭刚度，钢梁翼缘随桥面板变形受限，使得焊钉拉拔应力幅度增加。梁间荷载作用下工况L-6的焊钉最大拉拔应力大于梁间荷载作用下其他工况焊钉最大拉拔应力，悬臂端荷载作用下工况X-5的焊钉最大拉拔应力大于悬臂端荷载作用下其他工况焊钉最大拉拔应力，因此以梁间荷载作用下工况L-6与悬臂端荷载作用下工况X-5为2种加载模式下的最不利工况。

2.2 焊钉拉拔应力沿纵桥向分布规律

图8 T沿纵桥向分布

焊钉拉拔应力T沿纵桥向分布如图8所示，沿纵桥向荷载作用位置剪力槽内的焊钉拉拔应力最大。焊钉拉拔应力随着离荷载距离的增大而减小，并且焊钉拉拔应力沿纵桥向的衰减速度很快，距荷载作用位置0.562 5 m处的焊钉拉拔应力几乎为0。

3 焊钉拉拔应力参数分析

3.1 桥面板厚度与主梁间距比对焊钉拉拔应力的影响

研究梁间荷载最不利工况L-6与悬臂端荷载最不利工况X-5作用下，k1对双工字钢组合梁桥界面横桥向掀起效应的影响，基于ABAQUS有限元软件的双工字钢组合梁拉拔应力计算结果如图9所示(Tmax为焊钉最大拉拔应力)。2种不同荷载作用位置焊钉拉拔应力的变化趋势一致。随着k1的增大，焊钉拉拔应力逐渐减小，说明双工字钢组合梁的桥面板越薄，主梁间距越大，桥面板横桥向弯曲效应越明显，焊钉拉拔应力越大。

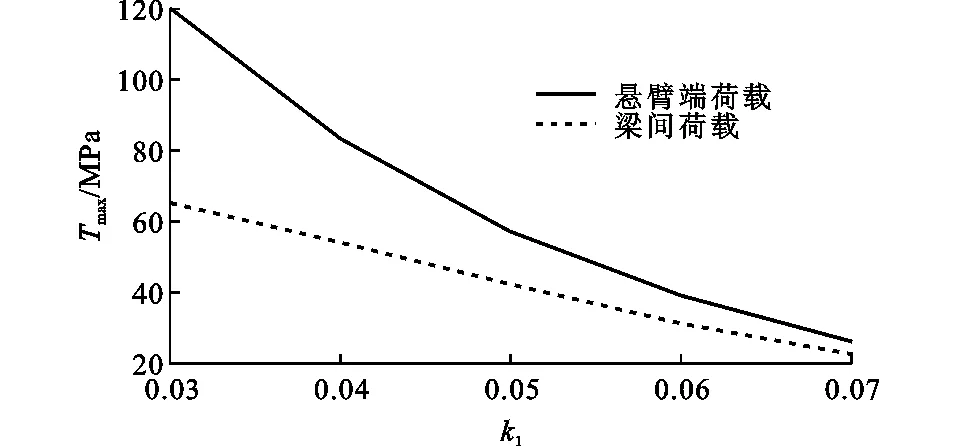
图9 Tmax随k1变化趋势

3.2 横梁设置位置对焊钉拉拔应力的影响

研究梁间荷载与悬臂端荷载最不利工况下，横梁设置位置对焊钉拉拔力影响。有限元数值计算结果如图10所示，2种不同作用位置的荷载工况下，k2变化对焊钉拉拔应力影响趋势相似。

图10 Tmax随k2变化趋势

当k2<1/2，即横梁位置处于一半钢梁高度位置以上时，如图11(a)所示，由于钢梁在横梁以下较大范围的侧向变形不能得到有效约束，此时钢梁侧向变形较大，焊钉拉拔应力较小。随着距钢梁上翼缘顶面距离Z的增大，钢梁扭转约束越明显，焊钉拉拔应力随之增大。

当k2≥1/2，即横梁位置处于一半钢梁高度位置以下时，如图11(b)所示，钢梁的侧向变形受到横梁约束，焊钉拉拔应力较大，且随着横梁距钢梁上翼缘距离增大，横梁对钢梁扭转约束能力增强不再增大，焊钉拉拔应力变化不明显。

当k2接近于1，即横梁位置较靠近下翼缘时，如图11(c)所示,横梁与桥面板间存在较大范围的钢梁侧向变形无法得到约束，焊钉拉拔应力略微减小。

图11 横梁位置对钢梁变形的影响

3.3 焊钉横桥向间距对焊钉拉拔应力的影响

研究梁间荷载最不利工况L-6与悬臂端荷载最不利工况X-5作用下，焊钉横桥向间距dj对焊钉拉拔应力的影响。

如图12所示，随着焊钉横向间距增大，焊钉应力出现先增大后减小的趋势，尤其是悬臂端荷载作用下，下降趋势十分明显。焊钉拉拔应力与横向掀起位移呈正相关关系[21]，相同的钢混界面分离程度下，焊钉横桥向间距越大，最外侧焊钉越靠近钢梁上翼缘边缘，该处焊钉横向掀起位移越大，焊钉拉拔应力越大，但同时焊钉越靠近钢梁上翼缘边缘，焊钉抑制钢混界面分离效果越明显，钢混界面的横向掀起位移越小，焊钉拉拔应力随之减小。受2个因素同时影响，焊钉拉拔应力随着焊钉横桥向间距dj增大，出现先增大后减小的趋势。

图12 Tmax随dj的变化趋势

3.4 各参数敏感性分析

为比较各参数对焊钉拉拔应力的影响程度，将焊钉拉拔应力变化率与参数变化率的比值定义为敏感因子η[式(3)]。敏感因子越大，说明焊钉拉拔应力受此参数影响越大，反之，敏感因子越小，说明该参数对焊钉拉拔应力的影响越不明显。

(3)

式中：f为基准参数下焊钉拉拔应力，取原设计为基准参数；Δf为不同参数下焊钉拉拔应力与基准参数下焊钉拉拔应力的差值；x为基准参数；Δx为参数与基准参数的差值。

各参数对焊钉拉拔应力的敏感性因子计算结果如图13所示，桥面板厚度与主梁间距比k1对焊钉拉拔应力影响最显著，焊钉横桥向间距dj影响次之，k2对焊钉拉拔应力影响最小。

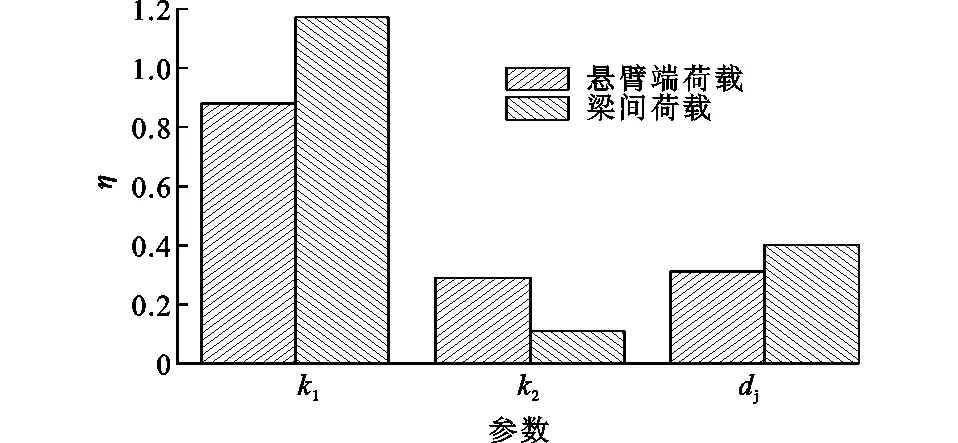
图13 焊钉拉拔应力对参数敏感性分析

4 结语

(1)拉拔应力产生的原因是加劲肋限制了钢梁上翼缘随桥面板的变形，导致焊钉轴向受拉，出现拉拔应力。沿纵桥向，焊钉拉拔应力在荷载作用位置最大，随着离荷载距离的增大而减小，且衰减速度很快，距荷载位置0.562 5 m处焊钉拉拔应力几乎衰减为0。因此，建议适当加密双工字钢组合梁在加劲肋附近的焊钉。

(2)对于双工字钢组合梁桥的焊钉拉拔应力，车轮荷载作用位置处设置横梁的组合梁焊钉拉拔应力比不设置横梁的组合梁焊钉拉拔应力有大幅提高，焊钉最大拉拔应力最多能提高317.97%。因此，建议设计时双工字钢组合梁在横梁处的焊钉应适当加密。

(3)焊钉拉拔应力随着桥面板厚度与主梁间距比k1增大而逐渐减小。受横梁位置对钢梁侧向变形影响，当横梁中心线距钢梁上翼缘顶面距离与钢梁高度比k2小于1/2时，焊钉拉拔应力随k2的增大而增大；当k2大于1/2时，拉拔应力随k2的增大变化不明显；当k2接近于1时，焊钉应力略微减小。随着焊钉横向间距增大，焊钉拉拔应力呈现出先增大后减小的趋势。各参数中，焊钉拉拔应力对主梁间桥面板厚与主梁间距比k1最敏感，焊钉横桥向间距dj影响次之，横梁中心线距钢梁上翼缘顶面距离与钢梁高度比k2对焊钉拉拔应力影响最小。