斜交异形箱涵整体结构受力性能及变形规律

张 海，蔡玉军

(中铁第一勘察设计院集团有限公司，陕西 西安 710043)

0 引 言

箱涵结构具有良好的受力性能，对地基承载力要求较低，被广泛用于市政道路、地下通道、下穿公路和铁路等交通系统中[1]，但作为一种常用的地下结构，箱涵周围被土体包围，属于地下隐蔽工程，建成投入使用后不易观察其内部情况，检测维修难度大。此外，由于地下结构所处环境复杂，箱涵结构的力学性能受较多因素影响[2-5]，仅依靠结构力学等相关理论公式来描述众多复杂因素存在明显不足，不能准确反映箱涵结构的实际受力情况。

由于地下箱涵结构受力复杂，在部分重要的地下工程中常运用有限元软件建立箱涵模型，根据箱涵结构的边界条件和受力特征对箱涵弯矩、扭矩和变形等进行数值计算[6-8]，为实际工程提供理论指导。采用有限元分析方法能更准确地反映箱涵的实际受力情况，计算结果精度高，可大幅增加工程的可靠性。同时，还可以帮助设计人员了解箱涵的受力特性和变形规律，从而选择合适的设计方法，提高设计效率并保证整体结构的安全。目前主要有2种针对斜交箱涵的设计计算方法，分别是斜交转正交计算理论和斜交计算理论[9]。前者计算较为方便，可大大减少计算量，但该方法考虑不到钝角处的应力集中现象，导致计算结果精度不够；后者计算结果较精确，但其计算复杂，设计效率较低。目前，关于变形缝斜交对箱涵结构力学性能影响的研究较少，且研究对象多为形状规则、所处地质条件良好的箱涵结构[10-11]，而关于地裂缝斜交、异形、大跨、多跨、顶板及侧墙开洞等复杂工况下的箱涵结构研究几乎没有。因此，开展相关研究对指导实际工程应用具有重大意义。

本文结合西安站改扩建工程，以其中某大跨度三孔斜交箱涵地下通道为研究对象，采用有限元软件ABAQUS建立箱涵整体结构三维实体模型，分别在正常状态和极限状态下对其进行数值模拟，重点研究2种状态下箱涵通道的受力特性和最终破坏模式，根据有限元模拟结果，分析箱涵各典型构件的应力、应变分布情况和整体结构的变形规律及整体模型的可靠性，对该三孔斜交箱涵的设计计算方法提出建议，为实际工程提供理论指导。

1 工程概况

西安站新建地下通道为旅客出站和连接南北广场的主要通道，是西安站改扩建工程的重要组成部分，其中北侧站房和东配楼间的地下通道采用三孔箱涵形式。箱涵跨径为11.0 m+24.0 m+11.0 m，中跨顶板及两中侧墙厚1.5 m，两边跨顶板及边侧墙厚1.2 m，底板厚度均为1.5 m。受场地条件及整体规划方案的制约，西安f3地裂缝从三孔箱涵的中段斜向穿过，斜交角度约为25°，为了适应地裂缝的长期蠕动变形，根据《西安地裂缝场地勘察与工程设计规程》(DBJ61-6—2006)，拟在地裂缝处设置斜交变形缝，将三孔箱涵分成2段异形的箱涵结构。如图1所示，两箱涵斜交角度为25°，箱涵呈梯形布置，下底边约为63.0 m，出口处平面形状不规则，根据建筑功能和消防要求，在箱涵侧墙设置2列5.0 m×5.0 m洞口共7个，在箱涵顶板设置2排4.0 m×4.0 m洞口共8个。箱涵混凝土等级为C40，主受力钢筋和分布钢筋均采用HRB400级钢筋。为方便后续讨论，将图1箱涵平面示意图中下侧的箱涵编号为BOX-1，另一箱涵编号为BOX-2。

图1 箱涵平面、剖面示意图(单位：mm)

箱涵埋设于地下，四周被土体包围，承受包括涵顶填土、侧向均布土压力和侧向三角形水压力等荷载，采用PKPM软件对箱涵结构进行弯矩和轴力计算并配筋，负弯矩区(板墙连接节点)及各板跨中的配筋率见表1。在进行配筋设计时，箱涵BOX-2的分布钢筋和箱涵纵向平行，主受力钢筋垂直于分布钢筋；对于箱涵BOX-1，其分布钢筋仍平行于箱涵纵向，但主受力钢筋平行于变形缝，与分布钢筋的斜交角度为25°，钢筋布置示意图见图2。

表1 箱涵配筋率

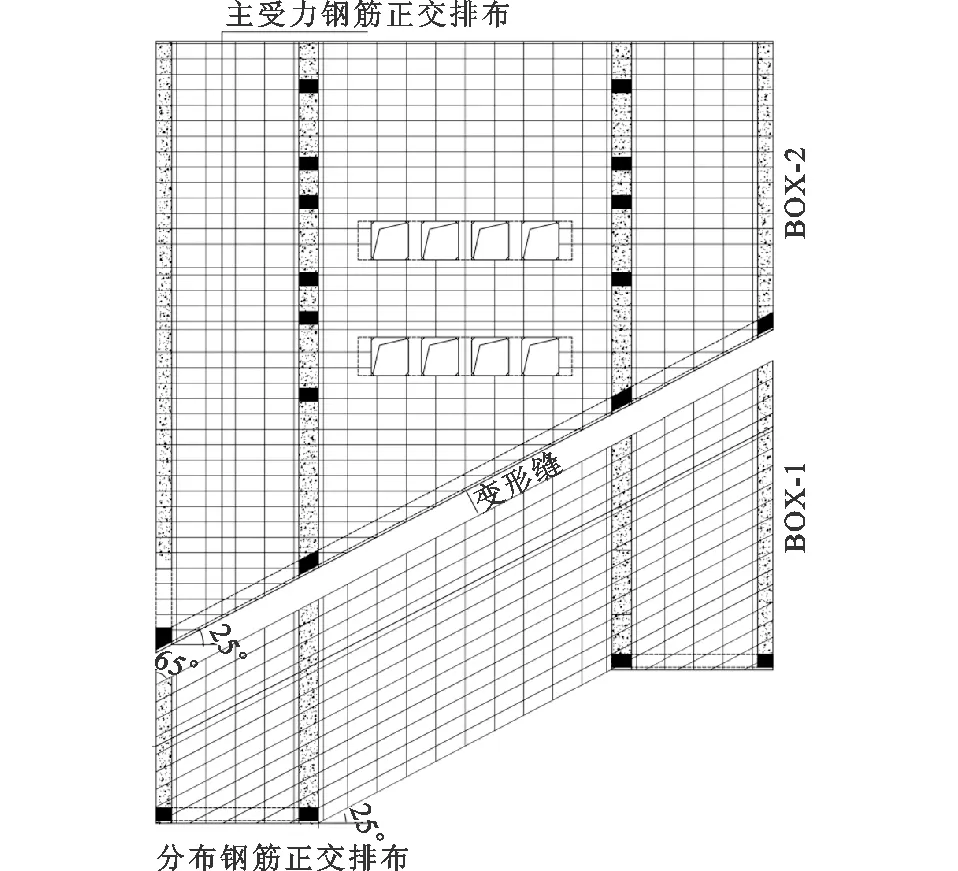
图2 配筋示意图

2 模型建立

2.1 混凝土和钢筋材料本构关系

图3 混凝土本构关系

混凝土塑性损伤模型的材料参数设定见表2。考虑有限元数值计算时的收敛性、精确性以及分析效率，黏性系数μ取0.000 5[15]。等双轴与单轴初始屈服应力比σbo/σco和拉压子午面第二应力不变量的比值KC均为ABAQUS软件默认取值，分别为1.16和2/3。

表2 混凝土塑性损伤模型参数

混凝土受压本构采用文献[16]的模型，受拉本构根据文献[17]以断裂能-裂缝宽度表征，用拉应力-裂缝宽度代替应力-应变曲线的下降段来描述混凝土软化行为，如图4所示，其中ft为混凝土抗拉强度，Gc为混凝土断裂能，wc为混凝土裂缝宽度。根据混凝土单轴受压和受拉应力-应变曲线可得到混凝土的名义应变和应力，但其不能直接输入ABAQUS中，真实的应力和应变还需通过换算公式进行换算[18]。混凝土拉压损伤因子di确定方式如下

(1)

式中：t,c表示受拉、受压状态；σi为应力；fi为材料强度。

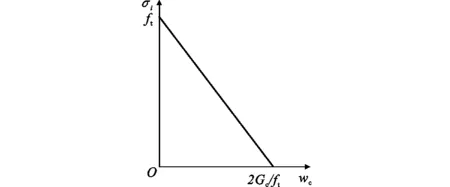
图4 混凝土受拉本构关系

钢筋采用理想弹塑性模型，该模型适用于流幅较长的钢材，其应力-应变(σ-ε)曲线见图5，其中fy为钢筋屈服强度，Es为钢筋弹性模量，εy为钢筋屈服应变。

图5 钢筋本构关系

2.2 单元选择

当结构承受弯曲荷载时，采用线性完全积分会造成单元过刚，导致结构弯曲变形不够，影响计算精度。同时，考虑到箱涵结构尺寸较大，配筋复杂，为节约计算资源，提高分析效率，本文中混凝土和钢筋分别采用空间三维缩减积分实体单元C3D8R和三维桁架单元T3D2模拟[19]，钢筋布置同实际结构，利用Embedded技术将钢筋埋入混凝土中。采用结构化网格划分技术建立混凝土网格划分，模型网格尺寸为1 000 mm×1 000 mm，BOX-1模型具有混凝土单元14 080个，钢筋单元205 278个。BOX-2模型共有混凝土单元28 212个，钢筋单元359 282个。2段箱涵数值模型如图6所示。

图6 有限元模型

2.3 边界条件

依据实际工程条件，采用荷载-结构模型确定边界条件。结构顶板及侧板直接施加结构实际承受荷载，在箱涵底部建立土体模型，假定结构与土体无相对运动，建立“Tie”约束，“绑定”结构底面与土体表面为整体，模拟底板边界条件如图7所示。土体采用C3D8R单元和莫尔-库仑材料模型完成建模。箱涵承受荷载包括地面活载、覆土自重、侧壁土压力和水压力等，由于箱涵顶面为花坛等园艺工程，无移动荷载，地面活载按静载考虑，为提高结构安全性，地面活载取值为20 kPa，各荷载值见表3。箱涵荷载模型见图8。

3 内力分析

在正常状态下对两箱涵实体模型进行数值计算，通过分析其应力分布和位移变形，研究箱涵正常状态下的受力性能及可靠性，箱涵正常状态荷载组合如图8所示。为探究箱涵的最终破坏模式和特点，将该荷载成比例放大，当主受力钢筋屈服时，视为箱涵结构达到极限状态[20]。

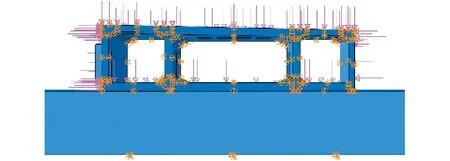
图7 模型边界条件

表3 箱涵各荷载取值

图8 箱涵荷载模型(单位:kPa)

3.1 典型构件分析

据数值计算结果，箱涵结构的分布钢筋应力远小于主受力钢筋，此处仅展示主受力钢筋应力及应变分布情况。

正常使用状态下箱涵整体结构的受力性能分析结果如图9所示。对于仅侧墙开洞的箱涵BOX-1，混凝土应力主要分布于顶板和两板墙隅角处，最大应力出现在顶板与开洞侧墙连接的隅角处，为9.35 MPa，另一隅角由于侧墙未开洞，截面未被削弱，应力较小；混凝土裂缝在跨中顶板底侧较集中，此时，顶板跨中底侧受力筋应力为187.2 MPa，钢筋仍处于弹性阶段。对于顶板和侧墙均开洞的BOX-2，顶板混凝土应力分布于顶板横截面跨中顶侧，主要为弯矩作用产生的压应力，且顶板洞口附近应力最大，为7.84 MPa；箱涵裂缝分布与BOX-1类似，主要分布于跨中顶板横截面底侧，裂缝平行于箱涵纵轴；受弯矩作用，箱涵钢筋最大应力出现在跨中顶板底侧的受力筋，为151 MP，钢筋同样未屈服，仍处于弹性阶段。

为探究地下箱涵的最终破坏模式和特点，将正常状态下的荷载成比例放大，当荷载放大至5倍时，主受力钢筋屈服，视为箱涵结构达到极限状态，极限状态下箱涵整体结构的受力性能分析结果如图10所示。由图10(a)～(c)可知，BOX-1裂缝主要分布于板墙相接的顶板顶侧、跨中顶板底侧和两隅角处，裂缝平行于箱涵纵向。箱涵结构中跨受弯矩作用影响较大，结构破坏时顶板底侧跨中开裂严重，内部连续墙外侧顶端受剪切作用出现裂缝，且侧墙与变形缝斜交处混凝土应力较大。由图10(d)可知，钢筋应力值由顶板跨中及隅角处向各自横向两端递减，位于中跨顶板和隅角的钢筋应力已达410 MPa，钢筋进入屈服阶段。由于数值模型忽略黏结滑移效应，可以看出顶板上层分布筋承受了部分压应力。由图10(e)～(h)可知，顶板和侧墙均开洞的箱涵BOX-2的裂缝分布与箱涵BOX-1相似，主要分布于板墙相接的顶板、跨中顶板底侧和两隅角处，但斜交端顶板底侧裂缝垂直于斜交边，而后平行于箱涵纵向。侧墙受剪切作用裂缝多集中于洞口两侧隅角处，而钢筋早已屈服，其塑性应变已达5.66×10-3。同时，连续墙洞口角部出现了扩大的裂缝区域，表明该处有应力集中现象。

图9 正常状态受力性能分析结果(单位:MPa)

3.2 整体模型可靠性分析

以正常使用状态下的数值计算结果对箱涵结构整体模型进行可靠性分析。

3.2.1 构件变形分析

箱涵BOX-1和BOX-2的各构件最大弯曲变形值如表4所示，其中三孔箱涵各构件最大弯曲变形分别发生在中跨的顶板、底板及两侧板。据《混凝土结构设计规范》(GB 50010—2010)[18]，正常使用极限状态验算时，受弯构件变形值需符合规范的变形限值要求。箱涵顶板(底板)变形限值为80 mm，侧板挠度变形限值为28 mm。由表4可知，箱涵各构件的最大位移变形值均远小于规范限值，符合设计要求，箱涵可满足正常使用。

图10 极限状态受力性能分析结果

3.2.2 混凝土和钢筋应力分析

箱涵BOX-1和BOX-2的混凝土和钢筋最大应力值及其相应位置见表5。箱涵结构混凝土强度等级为C40，其轴心抗压强度设计值fc为19.1 MPa，受力纵筋和分布筋选用HRB400级钢筋，强度设计值为360 MPa。由表5可知，箱涵BOX-1和BOX-2的混凝土和钢筋最大应力值均远小于规范限值，符合设计要求。

表4 箱涵各构件最大变形值

表5 箱涵混凝土和钢筋最大应力

4 设计建议

4.1 设计理论

图11为箱涵顶板底侧裂缝分布，箱涵BOX-1纵向长度较小，顶板底侧裂缝发展方向与箱涵纵向斜交；箱涵BOX-2纵向长度较大，顶板底侧裂缝靠近斜交变形缝时角度发生偏斜，而后主裂缝方向平行于箱涵纵向。

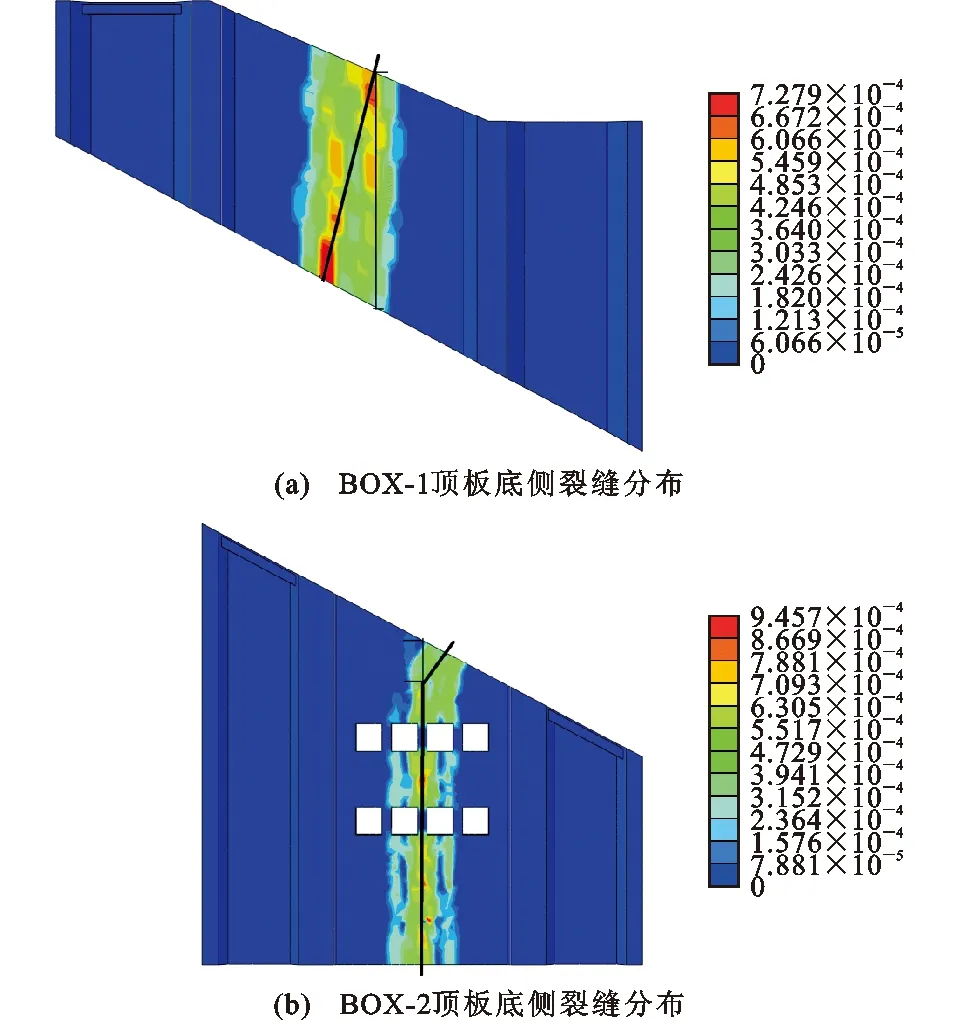
图11 箱涵顶板底侧裂缝分布

定义变形缝处斜裂缝沿箱涵纵向长度与箱涵跨度的比值为K。由于中孔跨度较边孔大，中孔顶板底侧混凝土在拉应力作用下开裂明显，此处主要考虑中孔的影响。对于箱涵BOX-1，K=0.77，对于箱涵BOX-2，K=0.23。在进行箱涵结构设计计算时，当K≥0.77或双侧变形缝斜交时，为提高计算精度，保证结构安全，建议采用斜交计算理论，斜交角为主弯矩方向与箱涵纵向的夹角；当K<0.77时，为简化计算，提高计算效率，建议采用正交计算理论，但随着K值增加，变形缝处斜裂缝沿箱涵纵向长度变大，此时采用正交计算理论会在一定程度上降低结构的安全性，为保证结构安全，应对斜交变形缝处采取构造措施进行加强。

4.2 构造措施

图12为两箱涵结构侧墙裂缝分布，结合箱涵在正常使用状态和极限状态下的有限元数值模拟结果可以看出，箱涵结构板墙连接的顶板处、板或侧墙开洞位置处以及板墙隅角处，尤其是结构与变形缝斜交的位置易出现应力集中现象。因此，可在洞口四周、板墙隅角和斜交段钝角处增设补强钢筋，提高箱涵结构局部强度，改善裂缝分布，板墙隅角处也可采用加腋处理。

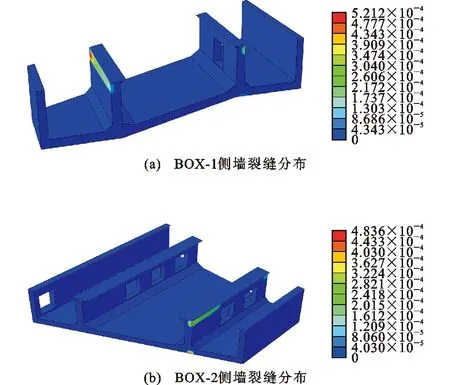
图12 箱涵侧墙裂缝分布

4 结语

(1)三孔斜交异形箱涵结构在荷载作用下的变形主要是顶板、底板的弯曲变形以及侧板的剪切变形。发生裂缝时，裂缝主要分布在顶板跨中底侧和板墙隅角，边孔混凝土和钢筋应力较中孔小。

(2)箱涵在正常使用状态下各构件最大变形值及混凝土和钢筋最大应力值均远小于规范限值，符合设计要求，结构安全，可满足正常使用要求。

(3)在进行斜交箱涵结构设计时，箱涵BOX-1建议采用斜交计算理论，斜交角为主弯矩方向与箱涵纵向的夹角；箱涵BOX-2建议采用正交计算理论，但应在斜交变形缝处增设补强钢筋进行加强。

(4)箱涵顶板和侧板的开洞区域、板墙隅角和斜交段钝角处易产生应力集中现象，应在相应位置增设补强钢筋，采取加强构造措施。

(5)当K≥0.77时建议采用斜交计算理论；当K<0.77时，建议采用正交计算理。K值未经大量多参数变化计算并验证，但对三孔、板墙开洞、斜交等类似工程仍具有一定的参考意义，针对具体实际工程时，还应结合工程具体背景和其他可能的影响因素进行研究和分析。