M估计下切尾均值和平尾均值的抽样分布

文小波

(四川民族学院 理工学院,四川 康定,626001)

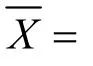
1 M估计与相关预备知识

为了方便论述,首先介绍一些相关的预备知识。

引理1[6]设x1,x2,…,xn是来自具有密度函数为f(x)的总体X的一个样本,EX=θ,DX=σ2,样

2 切尾均值的渐近分布

3 平尾均值的渐近分布

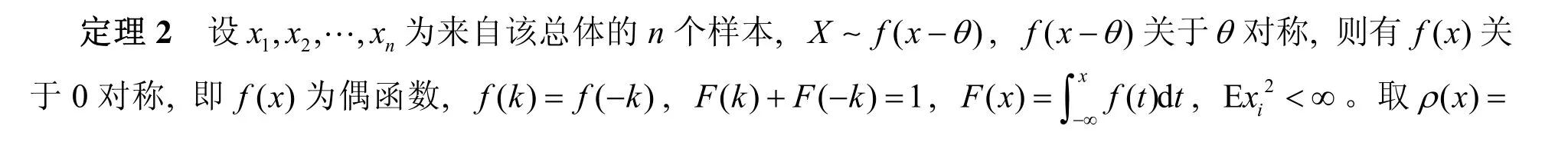
4 切尾均值与平尾均值的的极限状态的讨论

4.1 当k→+∞时的切尾均值与平尾均值的极限状态

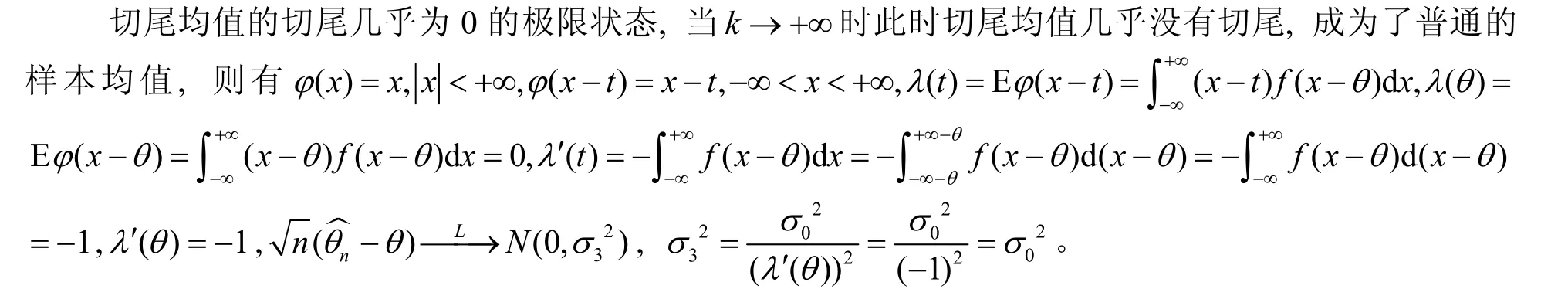
即此时切尾均值的渐近正态分布的方差就是普通样本均值的方差。同理可以有平尾均值在切尾几乎为0的极限状态时,此时几乎没有切尾,即几乎没有以切尾处临近值代替求解平尾均值的情况发生,此时平尾即成为了普通的样本均值,则其渐近正态分布的方差就是普通样本均值的方差。

4.2 在k→0时平尾均值的极限状态

5 举例分析

6 小结

由上述可知当n较大时,样本均值、中位数、切尾均值、平尾均值皆有渐近正态性。在总体分布关于θ对称时,其渐近期望皆为0,的渐近方差有所区别。在不同的总体,不同的样本在上述4个样本特征数各有自己的优势。