基于时差收敛算法的声发射源定位方法

2020-04-23张延兵宋高峰

无损检测 2020年4期

张延兵,宋高峰,朱峰

(1.江苏省特种设备安全监督检验研究院南通分院, 南通 226011;2.东南大学机械工程学院, 南京 211189)

基于声发射(AE)信号到达时差的定位计算是声发射检测中最为常用的定位方法，其主要原理为将声发射信号超过信号采集门槛值时声发射信号到达传感器的时刻作为参与定位计算的起始时刻，进而获取声发射源的准确位置坐标[1]。此种定位方法，在传感器信噪比较低、声发射信号在介质中的距离衰减、实际构件中不同方向声波传输速率的差异、结构不连续带来的波形畸变等诸多因素的综合作用下，数据采集门槛设定值与检测仪器灵敏度间会出现不匹配而引起较大的定位误差。针对上述问题，笔者尝试采用一种基于收敛算法的AE源定位方法，通过对基于声发射信号到达时刻的定位结果进行循环迭代计算，使得可以参与某声发射事件定位计算的各定位组重构的位置坐标，越来越接近收敛于同一点(或区域)，并最终实现理想精度的定位结果。

1 延时对算法定位精度的影响

传统的声发射激励响应时间测量方法主要采用门槛分析法[2-3]，即根据材料的塑形特性、现场检测环境(如噪声)、检测仪器配置、加载方式等因素综合选取检测门槛值，最终将传感器获取的信号第一次超过门槛的时间，作为AE信号首次被接收的时刻，并据此计算各通道采集到的声发射信号到达时差。在实际的计算过程中，阈值电平的设置会直接影响到最终声发射源定位结果的精度。为分析此问题，以声发射中较为直观的线定位试验进行论证分析，将传感器S1、S2相距100 mm成直线布置，并在两个传感器之间的P点进行激励，P点与S1距离为70 mm。

图1和图2为S1、S2采集到的声发射信号波形，分别记为x1和x2。根据实验室环境及试件材料选取检测门槛值为0.019 96 V，此时两个传感器测得的信号到达时差为9μs;当调整检测门槛值为0.034 0 V时,两个传感器测得的信号到达时差为11μs。依据上述数据计算信号源的位置,所得的定位结果如表1所示。

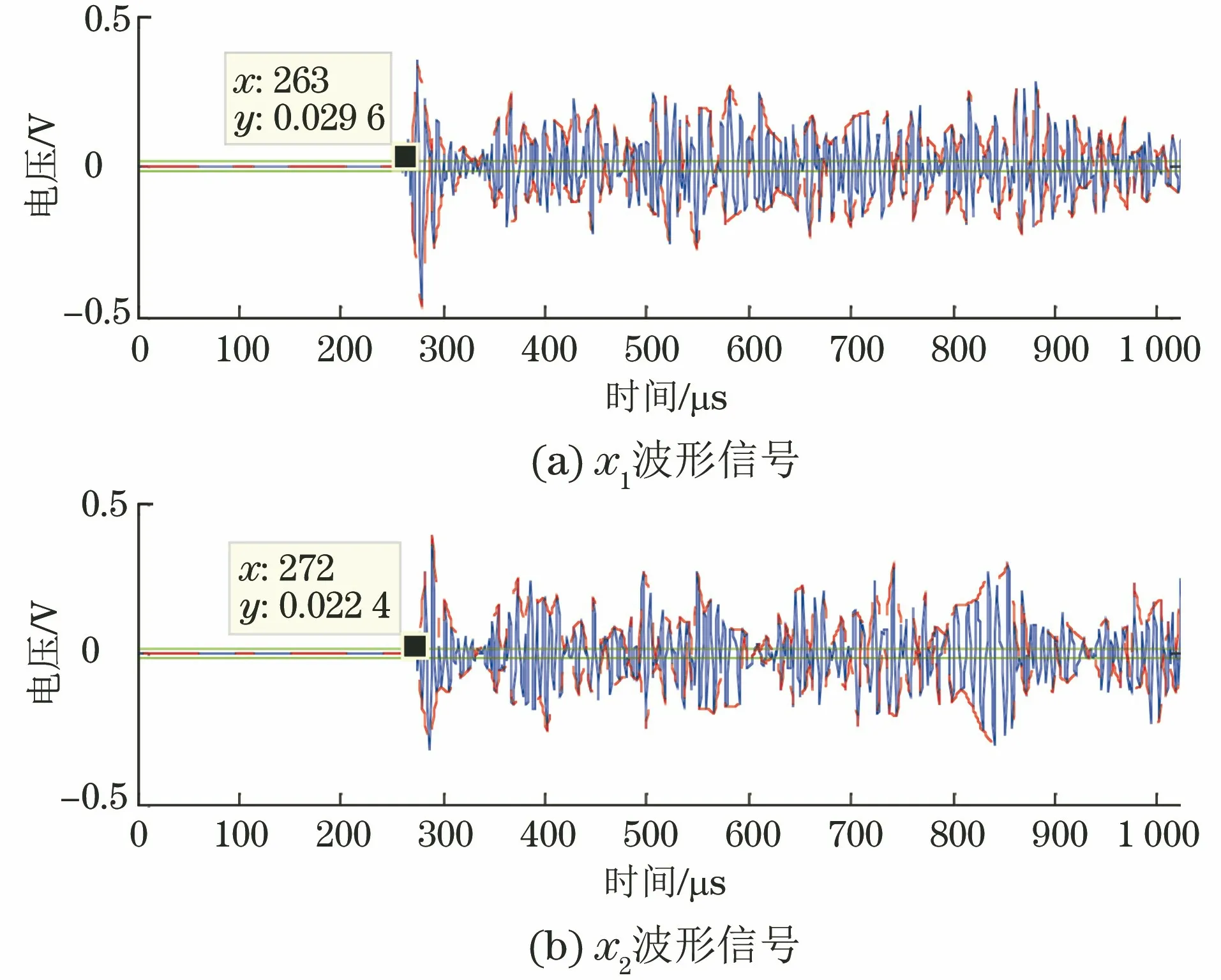
图1 声发射波形图(门槛值为0.019 95 V)

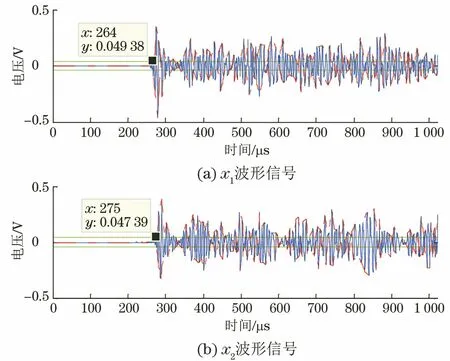
图2 声发射波形图(门槛值为0.033 9 V)

表1 声发射线定位结果分析

从表1可见，信号采集门槛的差异，导致定位源位置出现了较大的偏差，相对于定位组最远两个传感器间距100 mm，其比例已近7.5%，这显然不符合NB/T 47013.9-2015 《承压设备无损检测第9部分声发射检测》中5%的要求。通过以上分析可知，采集门槛的选择稍微有所不同都会导致定位精度的较大偏差，而采集门槛的选择受到诸多因素影响，例如：传感器所处位置的环境噪声、结构类型、距离加载位置的远近等，在实际的检测中不可避免会选择适宜的信号采集门槛阈值，而这些微秒级别的误差，也会大大影响定位的精度。

为解决门槛阈值差异对于传感器时差获取的影响，也可以采用互相关算法[4]，其主要的原理为：对于相同的声发射事件，无论被多少个传感器接收，其信号在特性上具有很强的匹配程度，唯有信号在传播时会出现不同程度的衰减或信号模式变化，因此可以通过对其在时域内进行互相关计算，以确定信号相对于不同采集通道的到达时间，进而计算声发射源的精确位置。此种方法在细长型结构中的应用效果较好，但在面积结构、大型体积型结构，尤其是复杂结构件中，结构的不连续和材料的各项异性会使得声发射信号在传播过程中产生大量反射、散射、波形畸变与叠加效应等，信号特征相较于原始波形也就产生非常大的差异，此时简单通过相关计算时差的方法就失去了作用。对于此问题也有通过经验模态分解、小波分析[5]等方法提取有效声源信号的缺陷特征频段进行重构后，再进行互相关分析获取时差，从而提高声发射源定位精度计算结果的有效性[6]，但实际的工程应用效果还不是很理想。

2 收敛算法的声发射源定位方法

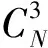
为测试收敛算法的声发射源定位方法，选取4个传感器进行试验，分别记为S1，S2，S3和S4，在某一区域进行一个信号激励，假定S2，S4，S3号传感器相对于S1号传感器的时差为T(Δt1,Δt2,Δt3)。将4个传感器中每任意3个作为一个定位组，得到4组定位数据，其编组信息如表2所示。

表2 传感器编组信息

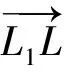
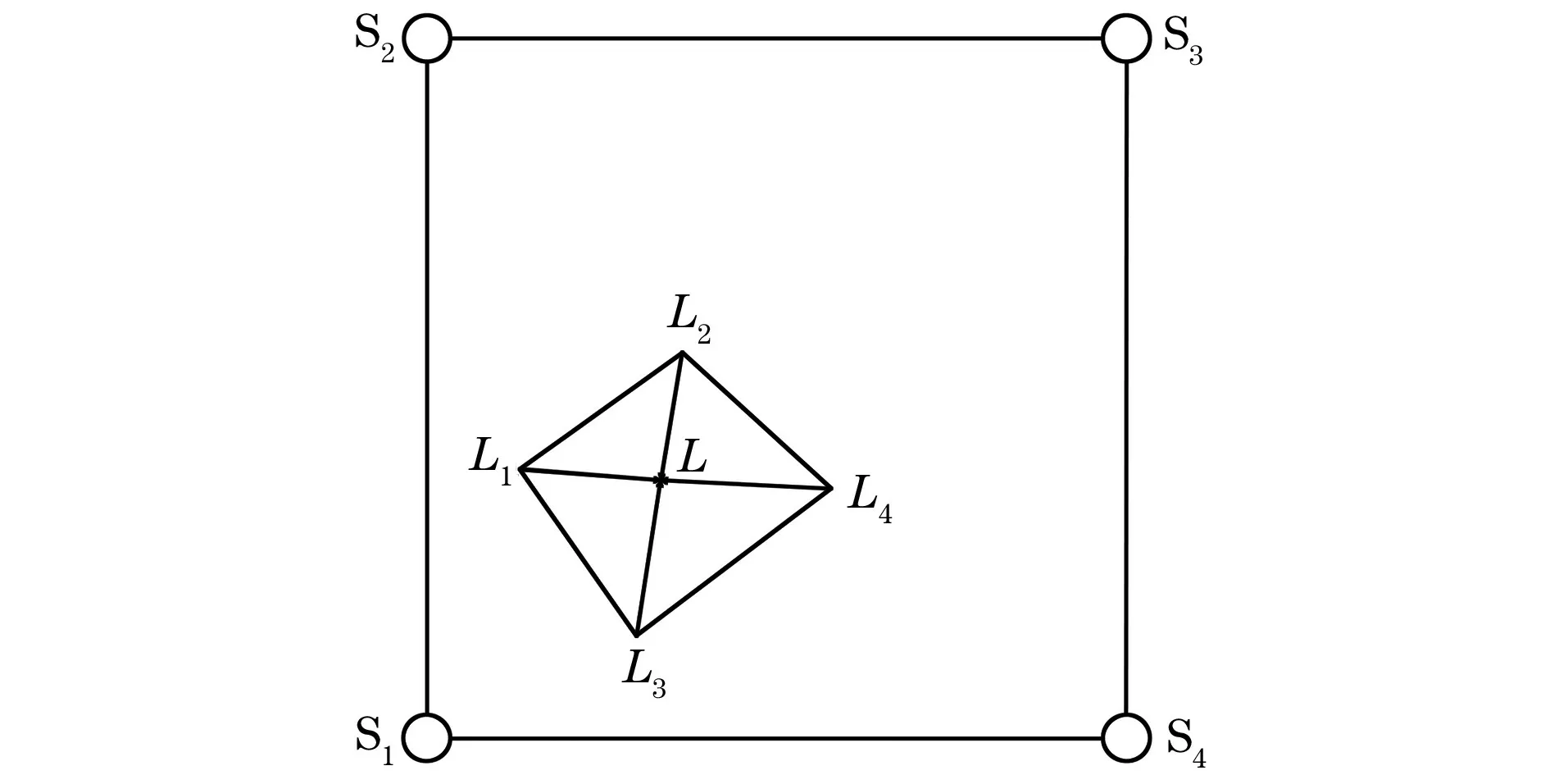
图3 声发射源定位点区域图

进而,可通过此次试验结果中4组定位的中心位置L反求出理想定位目标点的时差T′(Δ1,Δ2,Δ3)，如式(1)所示。

Δ1=(R2-R1)/v

(1)

式中:R1、R2、R3、R4为目标中心点L到每个传感器的距离(见图4)；v为波速。

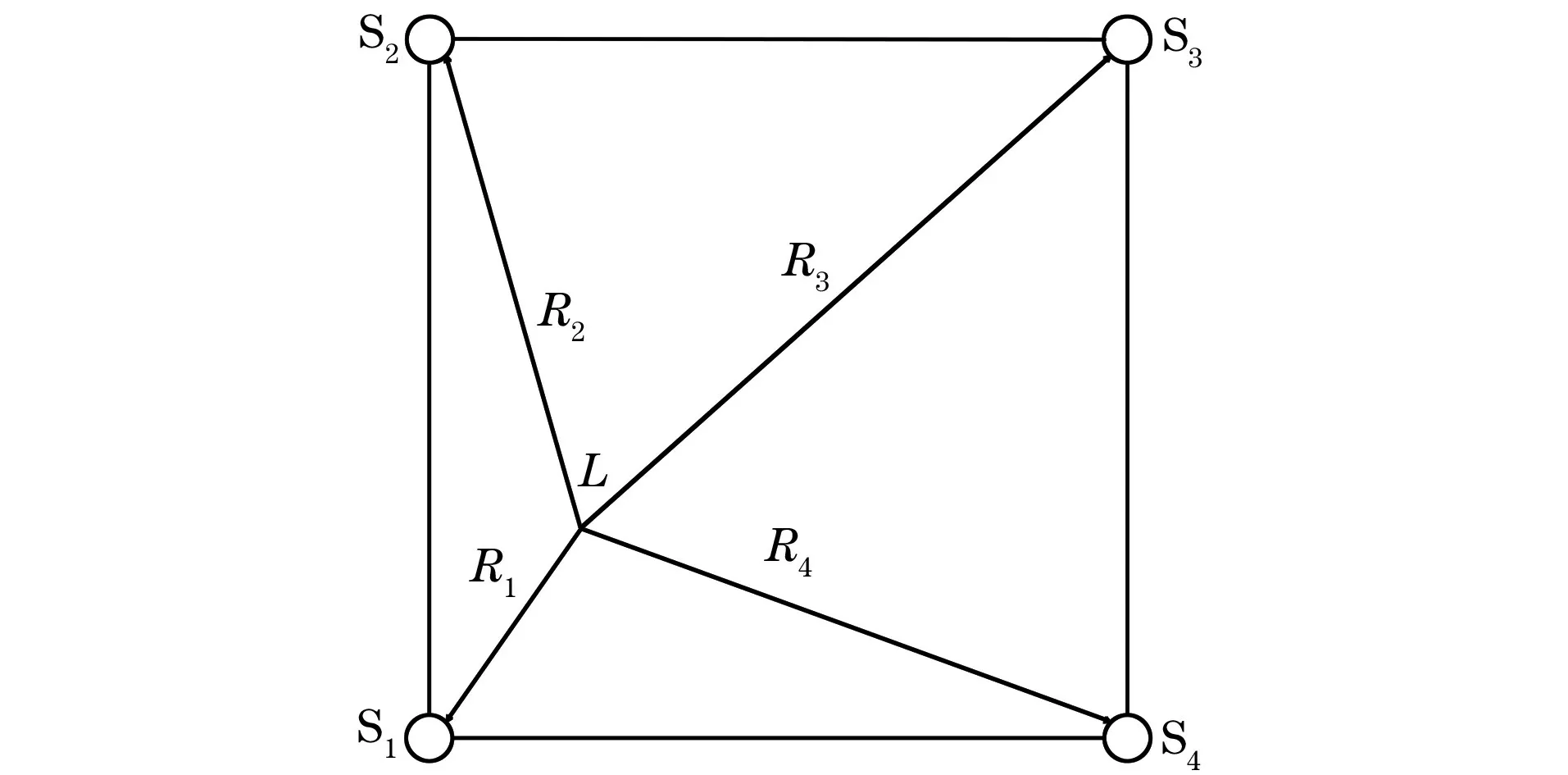
图4 声发射传感器布置图

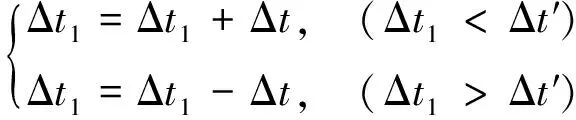
(2)

式中：Δt为修正步长，一般为0.050.5μs。

以此可类推修正Δt2,Δt3的值，最后依据修正后的Δt1,Δt2,Δt3，用三角定位算法重新计算，得到新的4组声发射源定位L1,L2,L3和L4。重复上述步骤，直至四边形L1L2L3L4越来越收敛，最终接近于同一个区域。在此计算过程中，以四边形L1L2L3L4的边长和作为优化目标函数进行计算，即：

F(T)=d(L1,L2)+d(L2,L3)+

d(L3,L4)+d(L1,L4)

(3)

式中:d(L1,L2)为L1与L2之间的距离;d(L2,L3)、d(L3,L4)和d(L1,L4)分别为L2与L3，L3与L4，L1与L4之间的距离。

通过循环迭代计算，使F(T)函数渐趋收敛直至稳定，此时即可认为该算法在多定位组条件下重构的声发射源位置坐标最为理想且误差最小。算法的具体流程如图5所示。

3 断铅试验及分析

3.1 试验过程

为了从试验角度验证基于收敛算法的AE源定位方法的准确性，设计制造了一块正方形钢试板进行测试，传感器位置阵列如图6(a)所示，其坐标(单位为mm,下同)分别为(0，0)，(140，0)，(140，140)和(0，140)。各采集通道灵敏度测试结果显示响应灵敏度在±4 dB之间，传感器耦合性能良好。首先在试板上进行4次断铅试验，坐标分别为(40，40)，(40，100)，(100，100)和(100，40)，每个点测试5次。

图6 声发射源定位试验传感器布置

3.2 试验结果分析

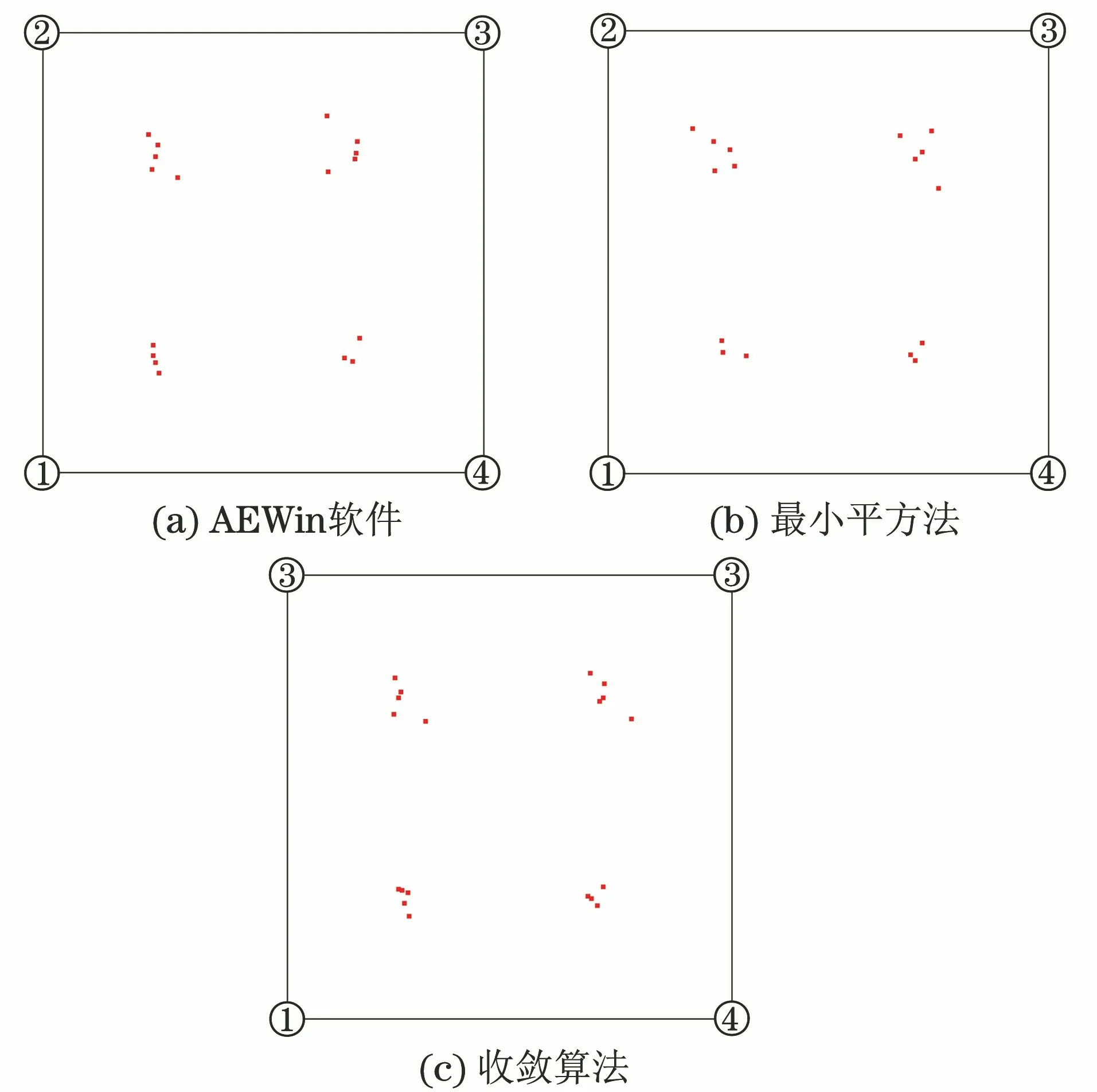
图7 3种方法的声发射源定位图

使用美国物理声学公司PAC的AEWin声发射采集系统进行试验，并对获取到的声发射检测数据进行解析处理，得到各通道采集到的声发射信号及相应的到达时间及定位数据。为验证新的定位算法的准确性以及其相对于传统时差定位的优势，试验通过收敛算法的声发射源定位算法对此次检测数据进行重构迭代计算，以形成新的定位源位置，从而与原有时差计算的位置进行比对。选择4组传感器进行定位测试，对于同一声发射源事件，每任意3组传感器均可进行独立的定位计算，将试验定位结果与最小平方法声发射源定位以及基于时差收敛算法计算的结果等三者进行对比。表3为AEWin系统定位结果，表4为最小平方法定位计算结果，表5为基于收敛算法的定位计算结果。图7为3种方法的声发射源定位图。

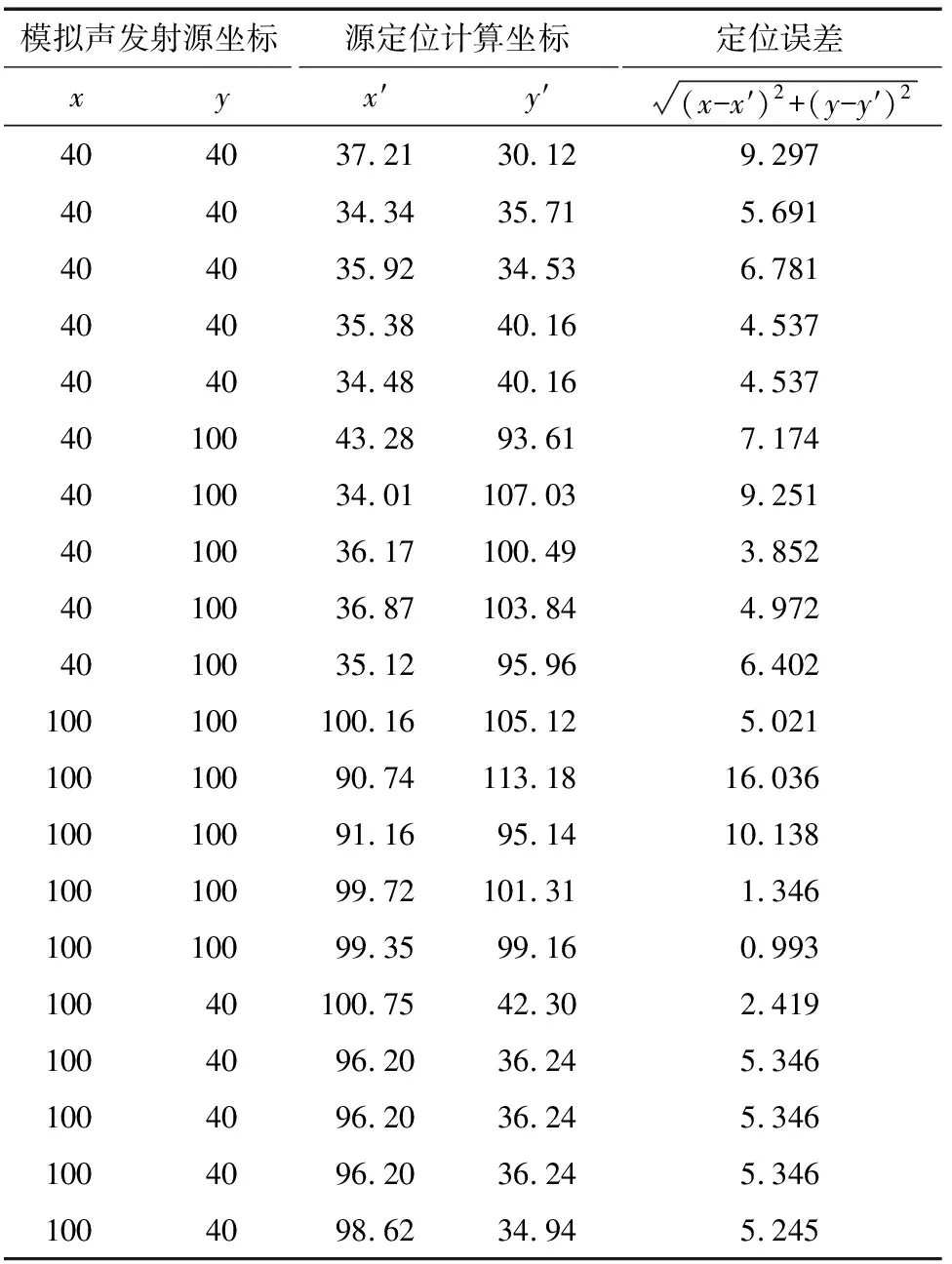
表3 AEWin声发射源定位结果 mm

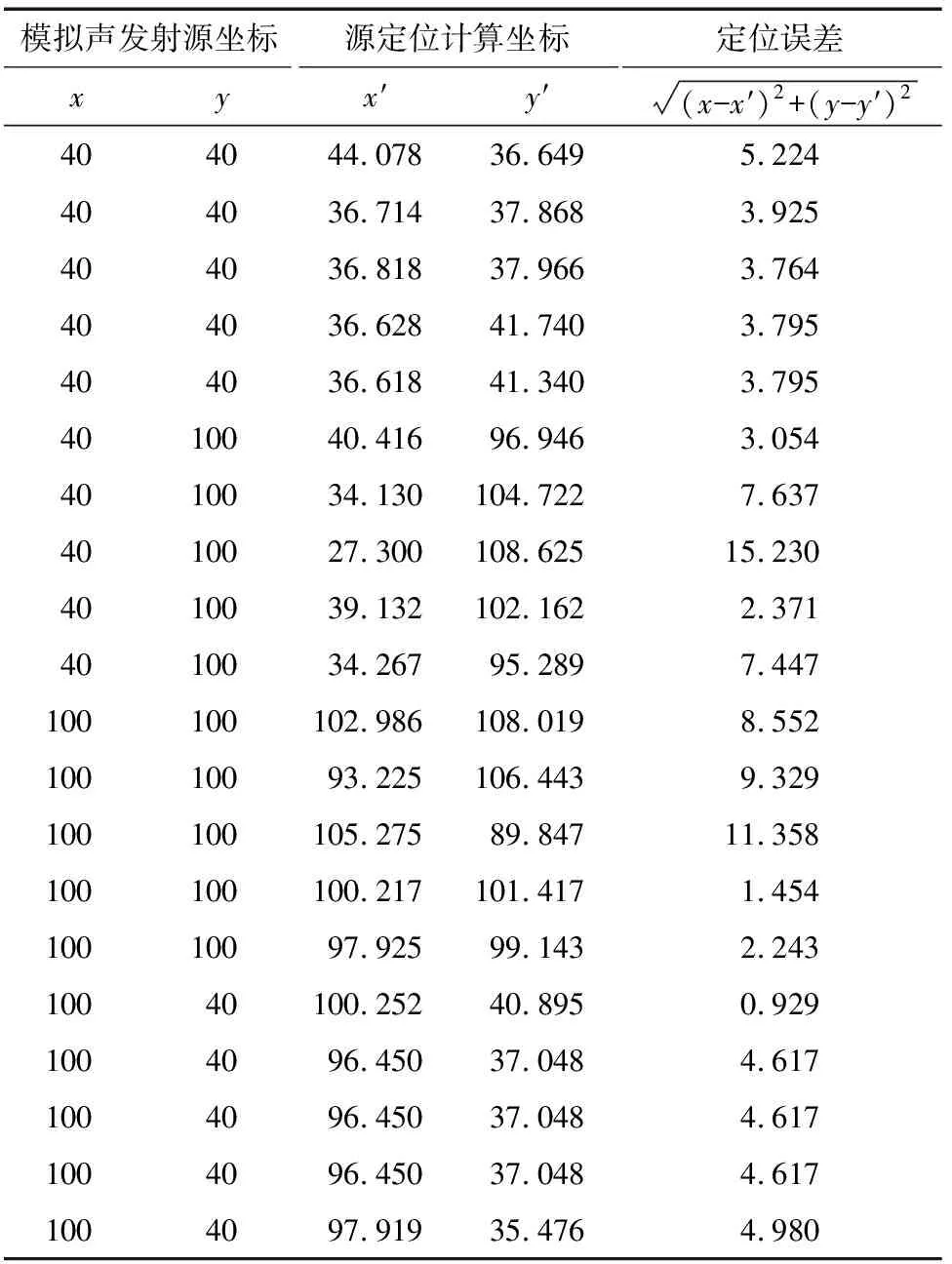
表4 最小平方法声发射源定位结果 mm

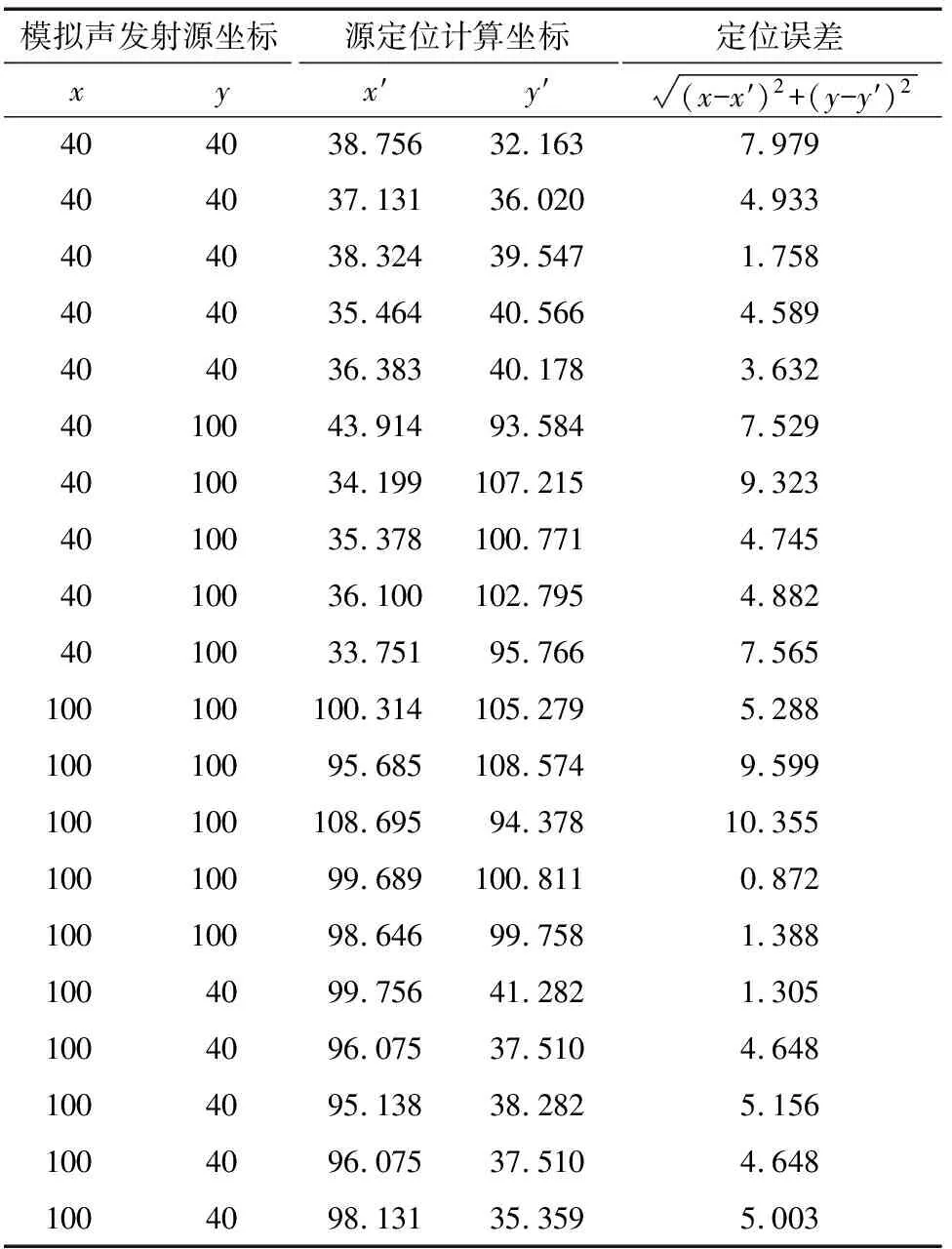
表5 基于收敛算法的声发射源定位结果 mm

由图7可以看出，基于收敛算法的声发射源定位方法获取的定位事件的集中度更好，而其他方法由于定位精度的差异，定位事件的离散度较高；另一方面，从定位误差(见表6)的均值和方差(与实际模拟声发射源的真实位置进行对比)也可以看出，基于收敛算法的源定位位置偏差明显小于其他两种方法的。而在实际的检测环境中，设备的尺寸和结构相对于试验试板的几何参数更大，型式更复杂，必然导致时差获取的误差大大增加，进而严重影响定位的精度。