大观念下指向学生核心素养的单元整体设计

闫红 张仰勇

为发挥教研工作对基础教育课程教学改革的专业支撑作用，提高教育教学质量，教育部“课程教材发展中心”和“课程教材研究所”在义务教育阶段建立了6个学科教研基地。其中，小学数学教研基地由“北京教育科学研究院基础教育教学研究中心”来承担。2019年基地协同河北、天津、浙江、湖北、黑龙江、广东、江西、云南、宁夏等省市，以“单元教学设计”为主题，开展了丰富多彩的研究实践。哈尔滨市清滨小学作为黑龙江省教研基地的研究团队，以“大观念下指向学生核心素养的单元整体设计”为主题开展研究，并结合“除数是两位数的除法”进行了单元整合的研究。

一、写在“整合”之前的学习和思考

1.何为“大观念”？

2018年1月教育部发布最新“普通高中课程标准”，强调以学科大概念为核心引领课程改革，促进学科核心素养的落实。随着“普通高中课程标准”的颁布，“义务教育阶段课程标准”的修订已经开始。国内学者也围绕“大概念”【英文Big Ideas（concepts），也有学者将其译为“大观念”，以下称“大观念”。】进行义务教育阶段的课程设置的研究。那究竟什么是“大观念”呢？

从学科教育角度，查尔斯（Charles. R. I）将数学大观念定义为：对数学学习至关重要的观念的陈述，是数学学习的核心，能把各种数学理解联系成一个连贯的整体，大观念使我们将数学看作是一个连贯的大观念集合。国内的专家和学者也对“大观念”进行了解读。北京教科院张丹教授认为“关于核心内容的本质、思想方法和教育价值的概括性、陈述性语句”即为“大观念”。天津教研室小数教研员任占杰老师认为，“大观念”指得是“从一类知识体系中凝练知识的核心、灵魂” 。从这些专家对“大观念”的解读中，能清楚地领悟到“大观念”是在对有“核心内容”“知识体系”的学习中，凝练出有关知识核心、本质的陈述性和概括性的语句。它能够引领教师确定单元学习的主题和学习过程中产生的具体观念。在这些概念理解的基础上，结合小学阶段数学学科的知识本质和思想方法，我们认为“大观念”在小学数学教学中可以具体表述为“数学核心概念的本质和思想方法的概括性语句”。

2.“单元整体设计”的意义何在？

《人是如何学习的：大脑、心理、经验及学校》一书中对学习过程的陈述是“必须用少量主题的深度覆盖去替换学科领域中对所有主题的表面覆盖，这些少量主题使得学科中的关键概念得以理解”。从其对学习过程的陈述中能够看出，用“少量”的学习主题替换“所有”主题，是学习必然经历的途径。深层理解之后，能感受到“少量”主题要有“深度”。这个“深度”就是能够涵盖知识本质和数学思想方法的“观念”，是要在这些“少量”主题中，能够融合指引学生长时间、持续学习的学习方法和思想方法，以便学生能够产生对“关键概念”的持久“理解”。这就需要“整合”单元学习内容，让学习更具备结构化的特征。

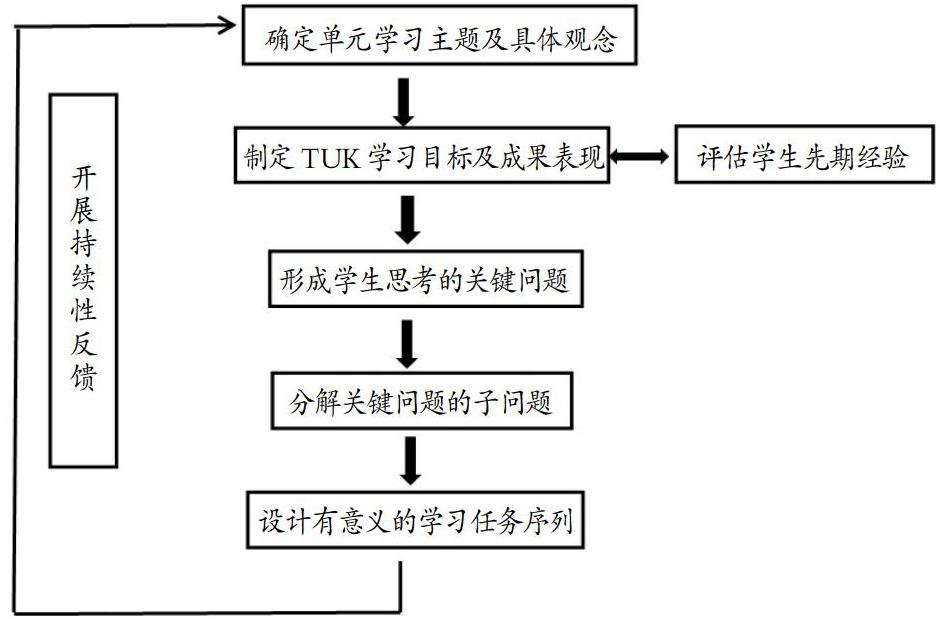
把这些理解融入到张丹教授解读的“观念统领”单元教学的基本过程中，我们能够清晰地看出，各个环节存在的不同任务。

“确定单元学习主题及具体观念”指向的是“大观念”的具体化的表述。

“制定TUK学习目标及成果表现”重点是“T目标”的呈现，也就是迁移目标，提醒我们应该多关注的是学生认知中“同化”和“顺应”现象的发生。学生学习中同化现象一旦发生，就意味着学生能够实现知识迁移，自主构建知识结构，学习能力也会相应提升。

“形成学生思考的关键问题”是单元具体观念的细化，需要从单元目标中剥离出学习主题的TUK目标和学生思考的关键问题。

“分解关键问题的子问题”是需要在充分分析学生学情之后，生成的能够促进学生学习的问题链。问题链中既有能够引发思考的铺垫问题，也有能够引领学生深度学习的关键问题。有了问题链，再设计有意义的任务序列就会变得简单和有依据，教师对课堂的把握会游刃有余。

3.对“观念统领”的学习预期。

在“大观念”引领下整合单元学习内容，对数学学习希望能够达成：

活——学生是在经历“活生生”的数学研究过程，而不是掌握“死”的数学知识。

通——学生能在自主學习和探究中，打通知识间的关联，形成知识间的迁移。

达——学生能简单构建知识模型，初步形成类比迁移的思想方法。

二、“除数是两位数的除法”单元整合

（一）单元学习主题及具体观念的确定

1.“除数是两位数的除法”的知识结构特点

从现行人教版教材，小学阶段有关“整数除法”的知识结构入手开展分析，制定“单元学习主题”，确定“具体观念”。

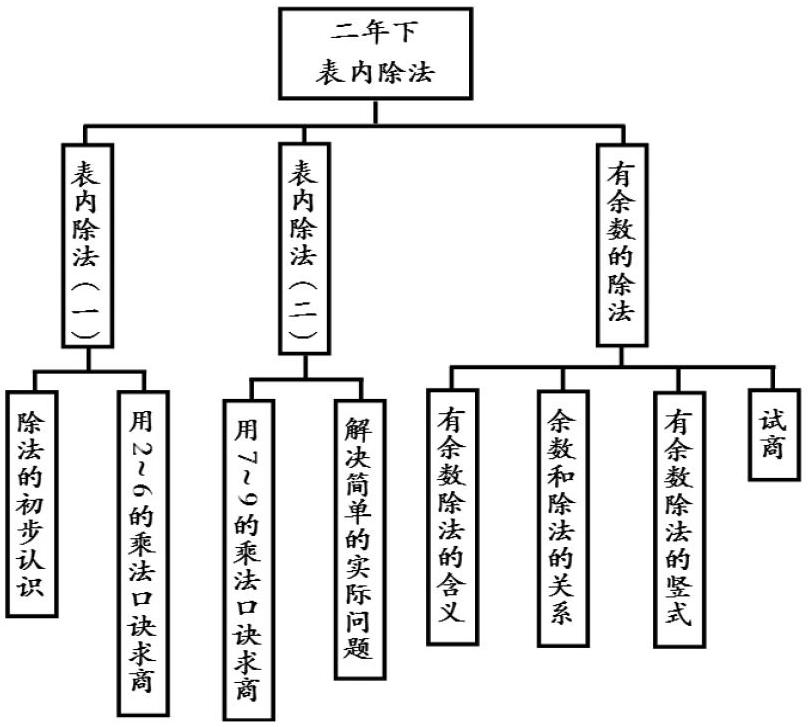
小学阶段有关整数除法计算的整体知识结构分为三个层次，分别是二年下（除法的认识）、三年下（除数是一位数的除法）、四年上（除数是两位数的除法）。

其中二年下，学生学习表内除法（一）时，就已经理解了除法的含义，理解了平均分。在表内除法（二）中，学生已经开始尝试运用“类比迁移”的思想方法，自己尝试探索计算方法。这是类比迁移思想方法在除法计算中的第一次运用。而在有余数除法中学生初次接触“试商”方法。

到了三年级下，学生完整经历了口算除法和笔算除法的学习过程，能够理解算理，掌握算法。在这种情况下到了四年级，学生还要学习哪些除法的相关知识呢？我们从现行教材四年上的解析中明确了本单元的学习要求：计算原理与除数是一位数的除法相同，试商的难度增大，掌握试商的方法。因为“原理相同”“试商难度增大”，所以可以用类比迁移的思想方法，构建“除数是一位数的除法”与“除数是两位数的除法”之间的联系，让知识学习呈现结构化的特点。综上分析，我们的思考是：

（1）怎样提高学生试商能力？

（2）怎么发展学生思维能力？

（3）如何整合单元学习主题？

带着这些思考，对现行教材的四年上“除数是两位数的除法”的相关学习内容进行了梳理。

2.“除数是两位数的除法”单元学习主题的确定。

（1）除数“是”整十数除法学习板块的整合。

现行人教版教材，四年上“除数是两位数除法”与三年下“除数是一位数除法”的单元结构十分相似，这也是现行教材考虑到学生学习中能够类比迁移的结果。但有些知识，学生已经有三年下的基础，在四年上再次出现，反而增加了知识点的数量，很难让学生掌握学习的重点内容。

例如，现行教材【人教版四年级上册71】在笔算内容之前安排了两个例题的口算和估算学习，其目的是为后面的“试商”做铺垫。笔算除法的例1和例2【人教版四年级上册73页】，利用“算除想乘”和“除法估算” ，解决除数“是”整十数的算理和算法。通过教学实践，我们能够发现学生在三年上解决整十数除以一位数时，就已经能够根据“一乘两除”的关系，会算整十数除以整十数的除法。而四年上的学习重点不在口算，而在除法估算。三年下学习的估算，估的是“被除数”的大小，到了四年上，估算能力要提到同时估“除数”和“被除数”，这样才能更好地为试商做铺垫。根据这种思考，我们把现行教材口算除法和笔算除法的4个例题，整合为“除数‘是整十数除法”学习板块。

（2）除数“非”整十数除法学习板块的整合。

现行人教版教材笔算除法的例3、例4、例5【人教版四年级上册76页、77页、81页】，都是利用“四舍”和“五入”的方法，使学生通过类比迁移，将除数“非”整十数除法转化为除数“是”整十数的除法问题来解决。而“调商”是计算技能的训练重点，用了两个例题来呈现。根据“观念统领”的教学思想，学生学习中应强化的是类比迁移和转化的思想，以此提升学生持续学习能力。而计算技能的训练，学生可以在练习中逐渐梳理总结，准确性和技巧性的掌握也需要长期的培养。所以，把这3个例题整合为“除数‘非整十数除法”学习板块，分为“调商”和“不调商”。

（3）“商是两位数除法”学习板块的整合。

现行人教版教材，例6、例7【人教版四年级上册83页、84页】的学习关联的是除数是一位数商是两位数的除法，目的是厘清商是两位数除法的算理、算法。而“观念统领”教学更关注知识系统的梳理提升和学习模型的建立。这样的学习能为后续进行更多位数的整数除法或小数除法的计算做铺垫。所以把这两个例题整合为“商是两位数除法”学习板块。

（4）对“商不变规律”内容的思考。

現行人教版教材例8、例9、例10【人教版四年级上册87页、88页】是“商的变化规律”和“简算”。史宁中教授在2019年10期《数学教育学报》发表了一篇题为《关于除数是分数或者小数除法的一个注》的文章，引起了我们的思考。文章中史教授认为：用“商不变的规律”解决小数除法问题，会让学生产生小数的乘法运算与除法运算不是一致的想法，学生很难感悟数学的运算是有逻辑的。根据史教授的想法，对“商不变的规律”本单元暂时不做整合安排。

根据对知识结构和教材的深度解析，我们把本单元的学习内容整合三个学习板块，并根据学习板块提炼了单元具体观念：

结合除法估算，借助数的组成进行算理、算法回顾。

利用“四舍”和“五入”法将除数“非”整十数 转化为除数“是”整十的除法问题。

通过类比（三位数除以一位数）解决商是两位数问题。着重经历模型建构和实际意义的理解。

（5）“除数是两位数的除法”单元内容整合前后对比。