发夹式换热器管束流致振动数值模拟研究
2020-04-22张天保王一鹏
谭 蔚,张天保,郭 凯,王一鹏
(天津大学 化工学院,天津 300350)
0 引言
发夹式换热器是管壳式换热器的一种特殊形式,具有单管程、单壳程结构,如图1所示,其管束及壳体均为U形结构,U形弯头与壳体焊在一起或者通过法兰连接[1]。发夹式换热器相比传统换热器具有诸多优点:管程和壳程的封闭体系适用于高温差、高压差工况;小流量高流速使流体产生高强度湍流,获得较高的传热系数,且固体壁面不易产生污垢;设备结构紧凑,生产制造成本低等[2]。作为一种紧凑式高效换热器,发夹式换热器在化工、核电等诸多领域应用越来越广泛[3]。
发卡式换热器的内部结构,如旁路挡板、折流板及支撑条的存在使得壳侧流体的湍流度较高。湍流流体与管束表面接触,流体中一部分能量转换为脉动的压力,因而会在相当宽的频带范围对管子施加随机的作用力激起管束振动[4]。工程上计算湍流激振响应时,首先需要根据壳侧流场信息来确定流体激振力的功率谱密度,进而求解管束在激振力下的振动响应。由于换热器实体模型较大,壳侧流场信息大多可以利用多孔介质模型进行数值模拟得到,如付磊等[5-8]均采用多孔介质模型,分别模拟了蒸汽发生器、折流杆换热器和弓形折流板换热器的壳侧流场。而对于用来度量湍流激振力的功率谱密度,国内外众多学者对其进行了研究,并提出了多种湍流激励功率谱[9-11]。

图1 发夹式换热器结构
目前,对于发夹式换热器的研究较少,其管束流致振动方面鲜有报道[12]。管壳式换热器管束流致振动计算大多基于GB/T 151—2014《热交换器》,但是此标准并未提及发夹式换热器,且发夹式换热器中U形管的弯管部分具有多组支撑条,不适用此标准中U形管的弯管部分不含支撑条或仅含单组支撑条的情况。本文以发夹式换热器作为研究对象,采用ANSYS CFX中的多孔介质模型对发夹式换热器的壳侧流场进行三维数值模拟,分析其流场特性,并结合流场信息,采用功率谱方法求解湍流激振力,进而模拟计算管束各节点的位移响应,为发夹式换热器的设计提供参考。
1 数值计算模型与方法
1.1 结构参数
本文研究的换热器为卧式,由地脚螺栓固定在基础上,管程和壳程流体均为液态水。换热管包括上下两段直管和一段弯管部分,管束的上下直管段部分由折流板支撑,弯管段部分由支撑条进行约束,管束排布方式为正三角形排布。部分结构参数如表1所示。
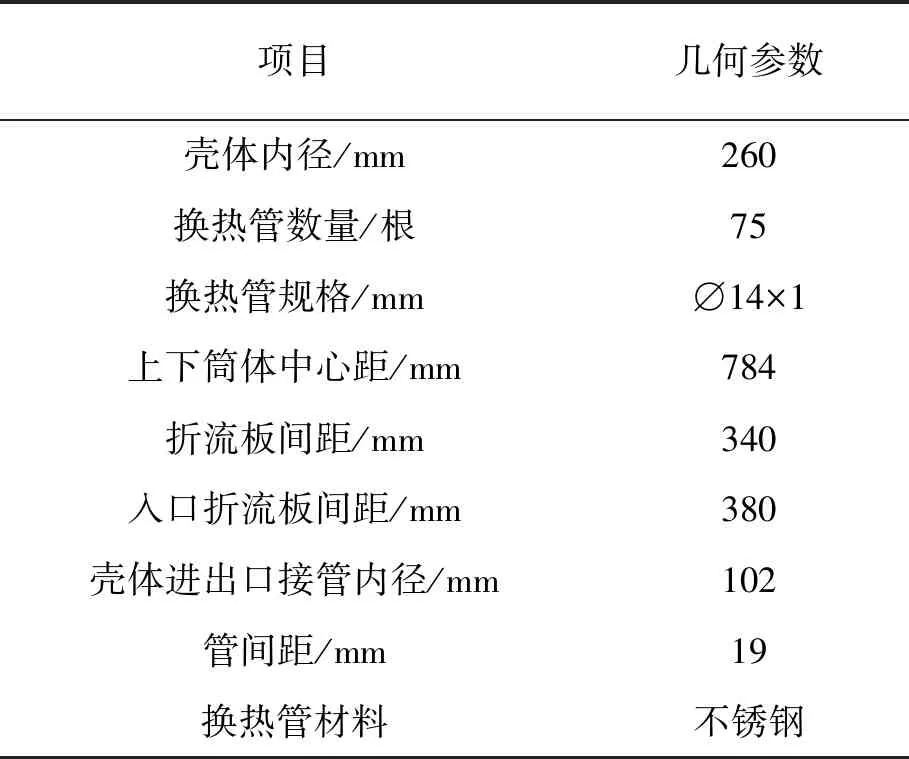
表1 换热器结构尺寸
1.2 多孔介质模型
发夹式换热器壳侧流场的模拟计算基于多孔介质模型,表示流体流动方程的通用表达形式为[13]:
(1)
式中ρ——流体密度,kg/m3;
f——容积多孔度,表示一个控制体积中流体部分所占有的体积,对控制容积的界面来说,表示表面渗透度;
φ——一般变量;
Γφ——φ的扩散系数;
Sφ——φ的源项。
依据换热器的结构参数建立多孔介质物理模型,对模型添加的主要边界条件为:管束区设置为多孔介质域,体积空隙率计算为0.504,其阻力系数由管束单元的压差曲线得到;壁面边界条件采用No Slip Wall无滑移壁面;流体域与多孔介质域交界面采用Interface交界面,网格连接方式为GGI;模型的流体入口为速度入口,流速为2.7 m/s,出口为压力出口,其表压力设置为0。
模型网格划分如图2所示。由于本模型存在较多交界面,同时含有复杂的曲面边界,因此完全采用非结构化网格。多孔介质域形状较为规则,采用六面体网格,流体域曲面较多,采用四面体网格,并对折流板附近的网格进行了局部细化。为了验证计算对于网格的依赖性,本文对网格总数为233万和798万的两种模型进行了对比。两种网格模型下第2跨的跨中流体速度分别为1.43和1.36 m/s,误差约为5.1%;压力分别为198 521和215 776 Pa,误差约为8%,因此认为误差相对较小,模拟计算比较可靠。
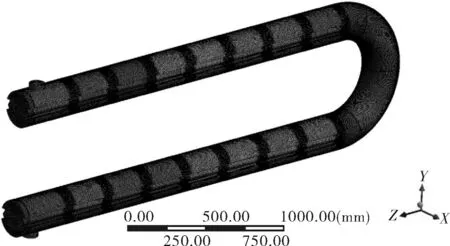
图2 计算模型网格划分
1.3 管束有限元模型
壳侧流体经折流板,反复横掠管束,管束受流体冲刷严重,容易发生流体诱导振动的危险。因此,以发夹式换热器的管束作为研究对象,利用ABAQUS软件建立梁单元模型,计算管束模态并求解管束在流体脉动冲击下的振动情况。
依据换热器结构建立管束的梁单元模型,管束材料属性如表2所示。文中换热器的管程和壳程流动介质均为液态水,管束有效质量为换热管结构质量、管内流体质量和附加质量之和,表2中的等效密度由此三部分转化得到。

表2 换热管的材料参数
假设管束的所有支撑条件均为有效支撑[14],则对模型施加以下约束:管束与管板连接处设置为固支,UX=UY=UZ=0,RX=RY=RZ=0;直管段与折流板连接处设置为简支,管束轴向可移动,UX=UY=0;弯管段与支撑条连接处设置为简支,管束周向可移动,UX=UY=0。
1.4 湍流激振计算方法
湍流激振时,管子在随机的脉动压力作用下呈随机振动,振动响应可利用经典的随机振动方程理论计算。本文利用文献[10]中功率谱密度计算方法求解升力和曳力方向上的湍流激振力。文献[10]中无量纲等效PSD的包络线可由下列各式求得。
升力方向:
(2)
曳力方向:
(3)
式中φL,φD——等效升力谱密度和曳力谱密度;
f——漩涡脱落频率,Hz;
D——管束外径,m;
vm——横流速度,m/s。
归一化功率谱为:
(4)
式中φ——等效功率谱密度,升力和曳力方向分别对应φL,φD;
F——流体力的功率谱密度,分为升力方向和曳力方向,(N/m)2·Hz-1;
ρm——流体密度,kg/m3;
l——计算段管束长度,m。
本文以每跨作为一个激振力计算单元,根据流场信息,以该跨的平均横流速度作为计算单元的输入条件,通过联立无量纲等效PSD的包络线和归一化功率谱,求得升力和曳力的功率谱密度。利用MATLAB程序生成随机信号,结合流体力的功率谱密度即可实现随动湍流激振力。使用有限元分析软件ABAQUS将湍流激振力作为载荷条件添加到需要计算的管束上,通过显式动力求解,即可得到管束的振动响应。
2 壳侧流场分析
图3为换热器对称截面上的速度云图。流体由入口进入壳程,经折流板后改变流动方向,并产生横向流,冲刷管束,从壳程出口流出换热器。可以看出,流体在第1跨区域流动时速度变化相对较小,经折流板后速度发生急剧变化。折流板迎流侧的速度变化强于背流侧,有利于迎流侧流体的传热。在每块折流板背流侧均存在涡流区,流体在此区域内处于相对停滞状态,使得此区域传热效率低,而且低流速下固体壁面容易结垢。在流体流经换热管弯管段时,由于不存在折流板的折流作用,该区域主要为轴向流,相对直管段流场比较均匀。
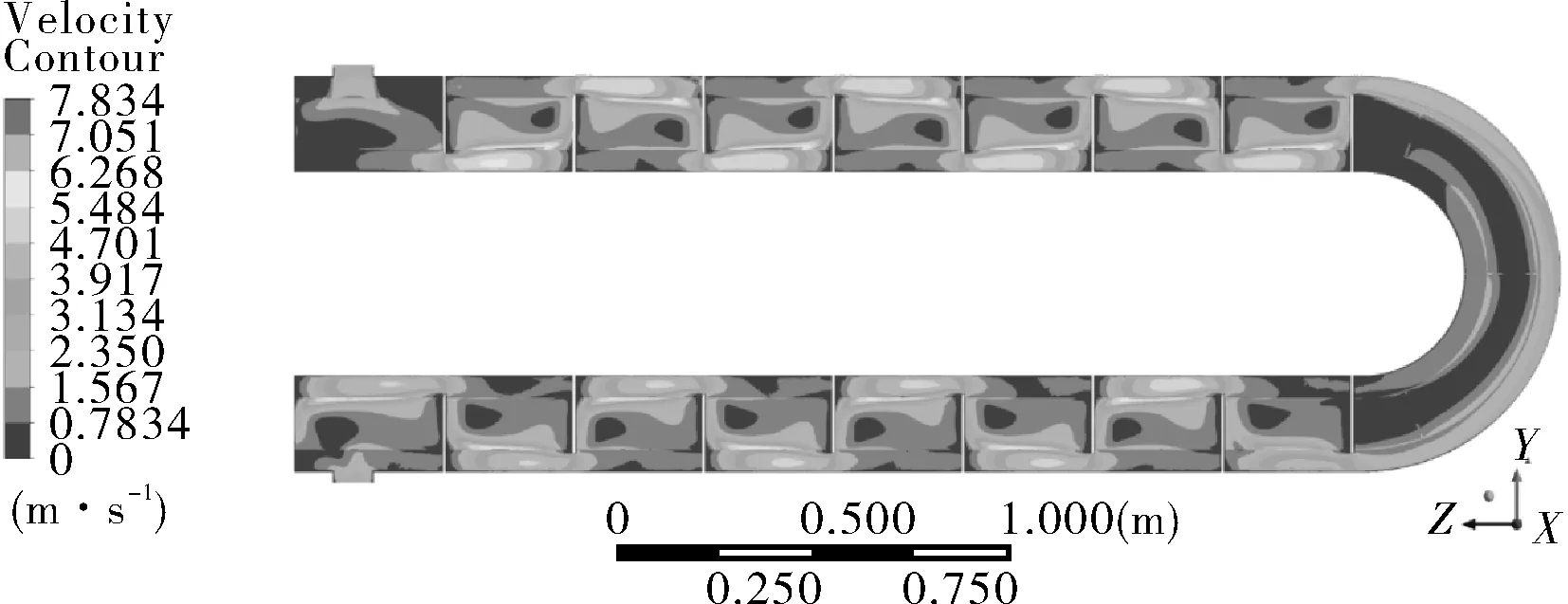
图3 换热器壳程速度云图
从图3中还可以看出,流体经折流板在壳程直管段部分反复绕流,在外层管束附近流速较高,说明此处管束受流体冲刷的程度最为剧烈。同时由于折流板的作用,该区域存在较高的横向流,横向流会严重冲刷管束,使管束承受流体力,易发生流体诱导振动的危险。提取最外层管束位置处的流速,如图4所示,可以看出流速分布与速度云图呼应,直管段流速分布曲线出现急剧变化,最高流速达到6.5 m/s,最低流速接近于0,而弯管区的流速分布曲线比较平缓。
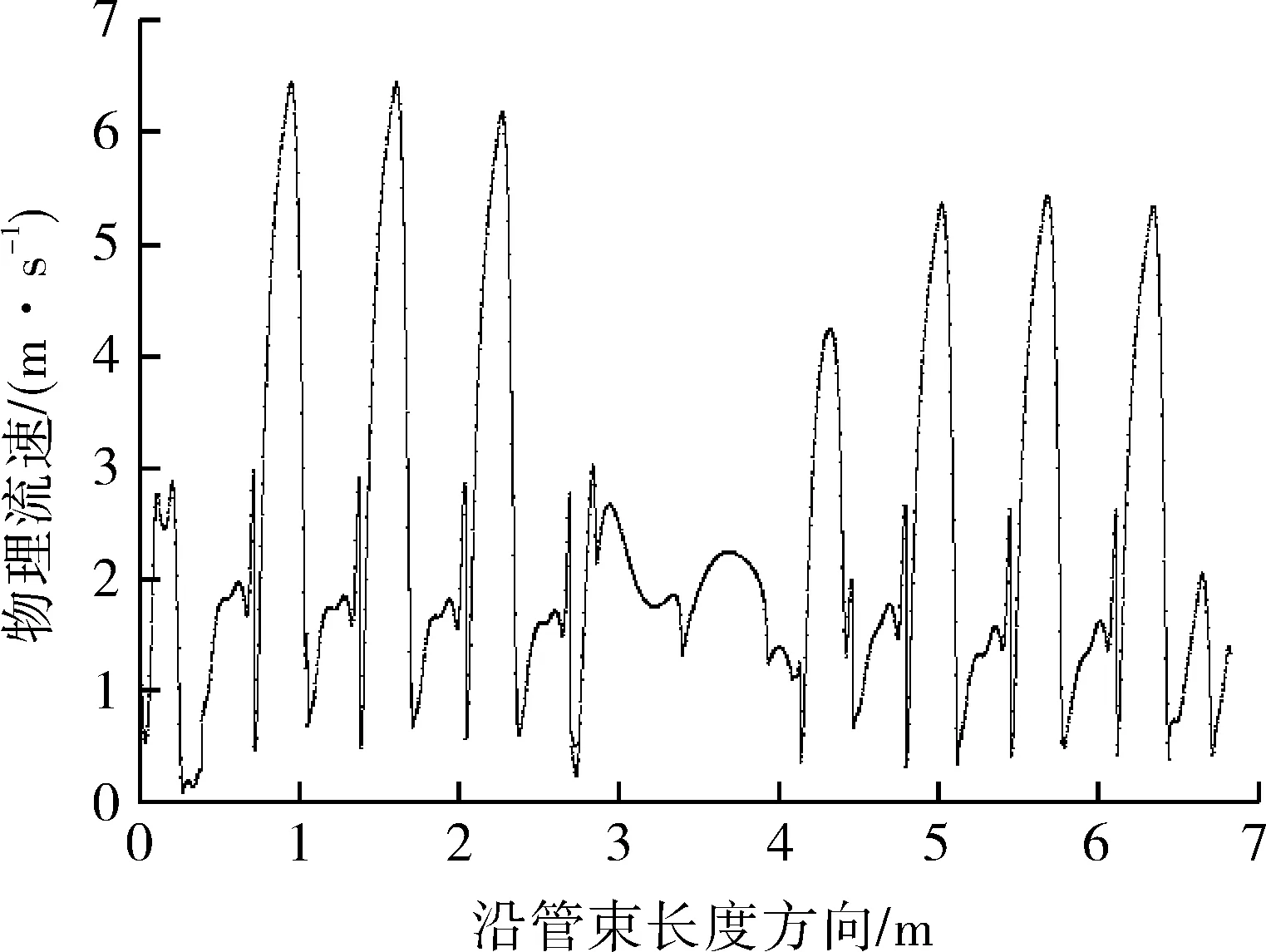
图4 换热器最外层管束区流速分布
3 振动分析
3.1 管束模态分析
根据换热管有限元模型,计算管束的前6阶模态,模态频率和管束振型分别如表3、图5所示。

表3 换热管束的前6阶固有频率

(a)1阶振型

(b)2阶振型
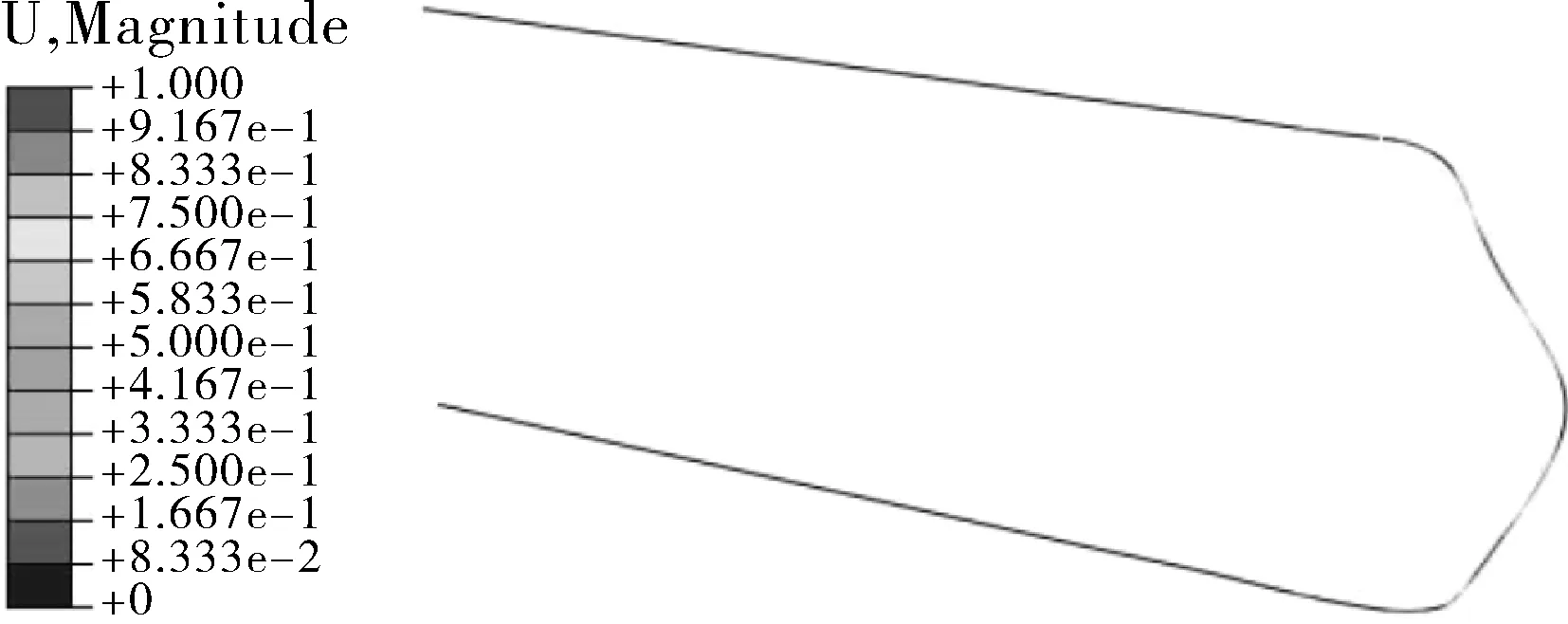
(c)3阶振型
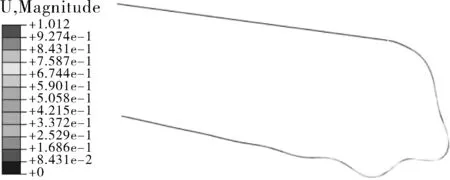
(d)4阶振型

(e)5阶振型
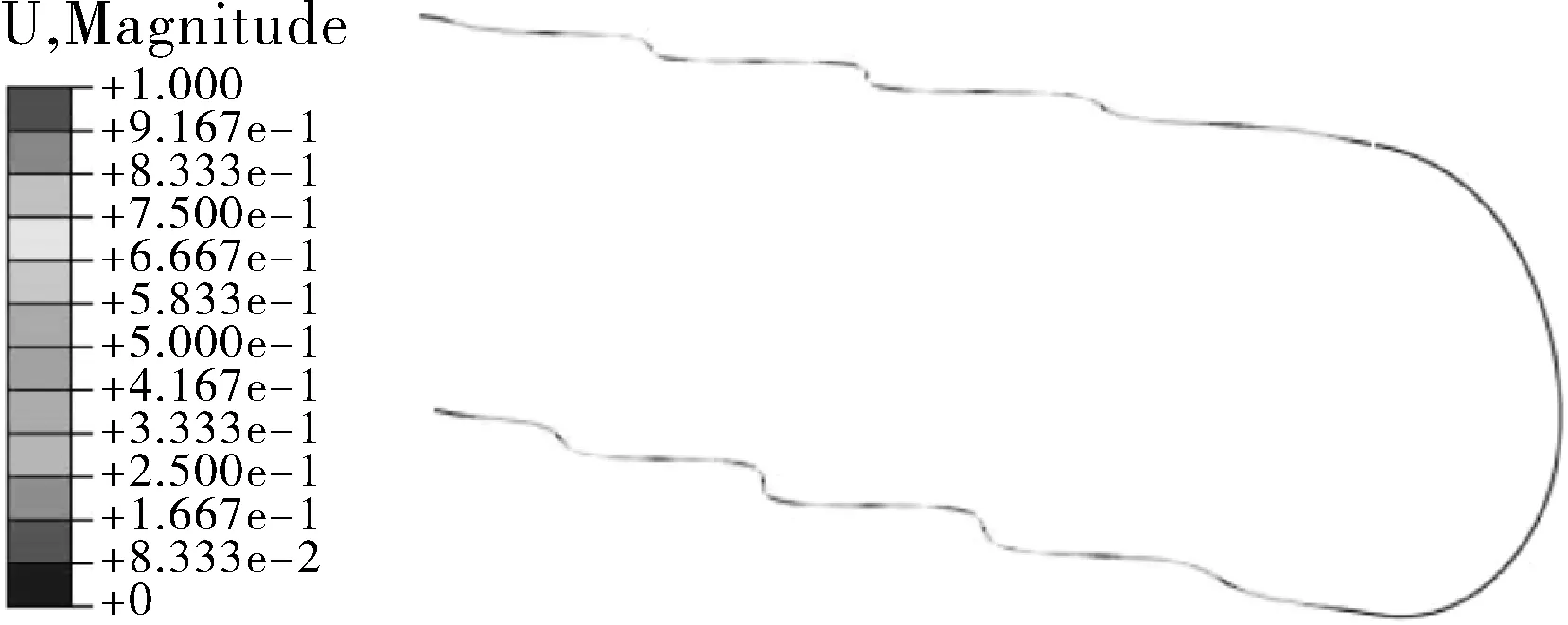
(f)6阶振型
由表3可以看出,管束的直管部分和弯管部分的频率差异较大。结合图5可以看出,管束的前4阶模态振型主要为弯管部分的振动,其中第1阶固有频率为77.57 Hz,表现为弯管部分的面内振动;第2和第3阶固有频率分别为98.94和153.24 Hz,均表现为弯管部分的面外振动;第4阶固有频率为196.50 Hz,表现为弯管部分的面内振动;第5和第6阶固有频率基本相等,分别为236.90和236.99 Hz,振型分别表现为直管部分的面内和面外振动。
3.2 振动响应分析
结合已知流场信息,利用流体力功率谱密度生成湍流激振力。以第一跨管束上的激振力为例,该跨平均横流速度vm=2.03 m/s,代入式(2)~(5)求得无量纲等效功率谱密度(见图6);经式(6)归一化功率谱求得功率谱密度(见图7);结合随机信号,进而得到湍流激振力(见图8),即升力和曳力。同样以此方法求解其他跨的激振力,并作为线载荷施加在管束相应位置。

图6 流体力无量纲等效功率谱密度的包络谱
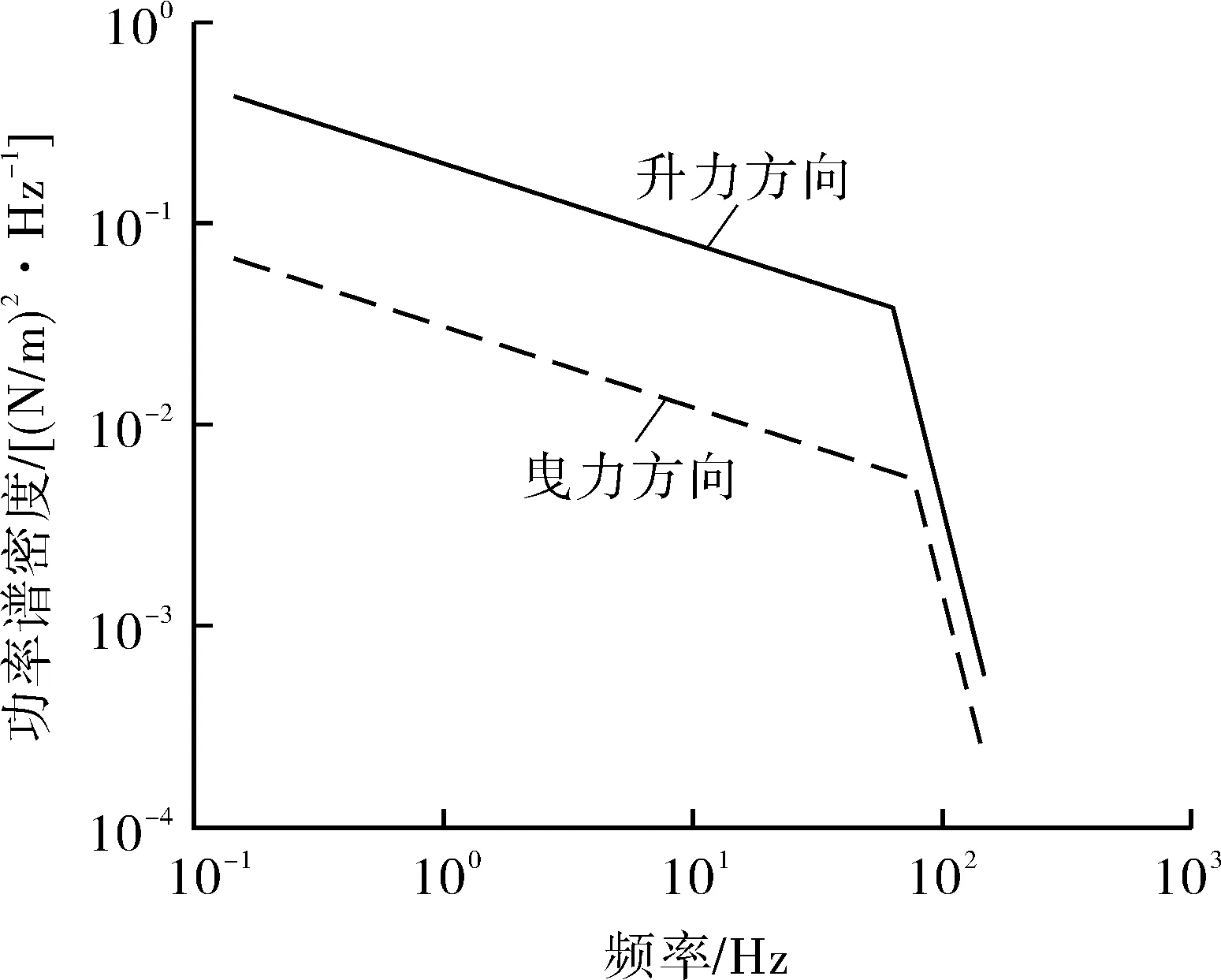
图7 流体力功率谱密度的包络谱
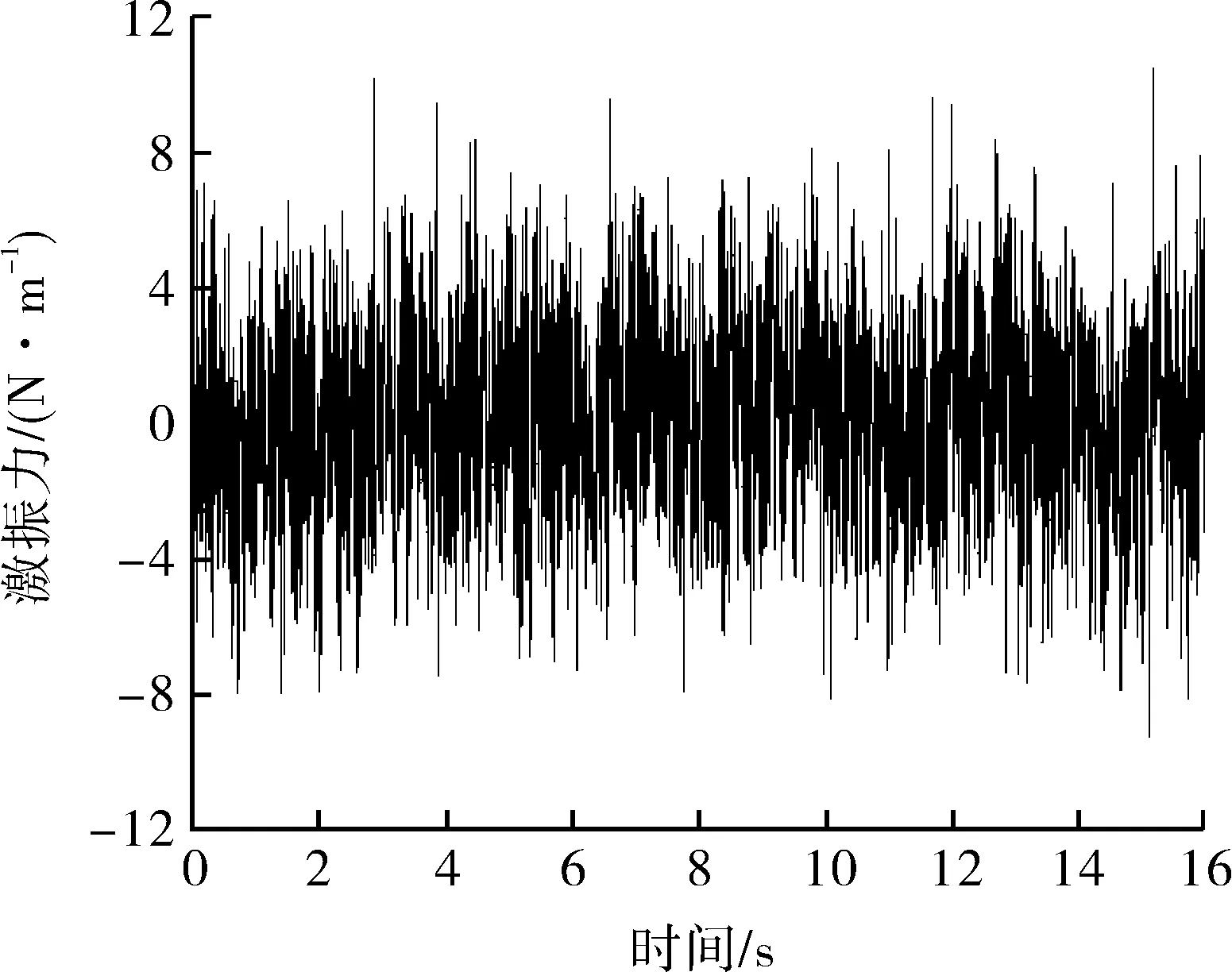
(a)升力方向
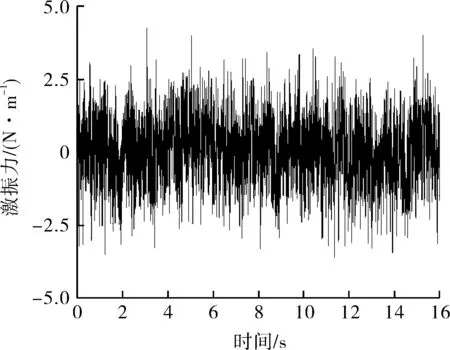
(b)曳力方向
本文模拟了管束在随机湍流激振下16 s内的振动响应,针对有限个测点信息进行分析。以U形管的约束点和每跨的中点作为测点,依次进行编号,共得到41个测点如图9所示,提取每个测点在15~16 s的位移响应,计算得到各测点在这1 s内的均方根总位移和面内、面外位移,如图10,11所示。
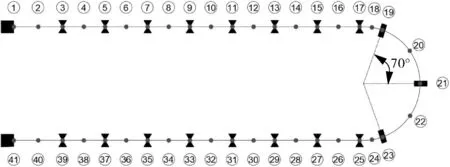
图9 测点位置示意
从图10可以看出,管束的均方根位移最大位置为测点20和22,分别为37.6和37.5 μm。这两个测点位于弯管的中间两跨,跨角分别为70°,跨长538 mm,是管束的最低模态的振型响应位置,刚度最低,因此这部分管束的振动位移最大。在20跨中,管束位移最小的为第9跨和第11跨,跨中位移分别为6.3和5.7 μm,对应测点18和23,这2跨为直管到弯管的过渡跨,跨距最小,振动位移也最小。由图10还可以看出,每跨中点的均方根位移远远高于约束节点处,这是因为除了管束两端采用固支以外,其他约束节点均采用简支,在X和Y方向不能移动,仅在轴向可以自由移动,即约束节点的位移是由管束轴向移动所贡献的。图11为管束在面内和面外的均方根位移。由图11可以看出,约束节点的面外和面内位移均为0,每跨中点的面外位移远大于面内位移,且面外位移折线走势与总位移走势基本一致,弯管区中间两跨的面外位移最大。
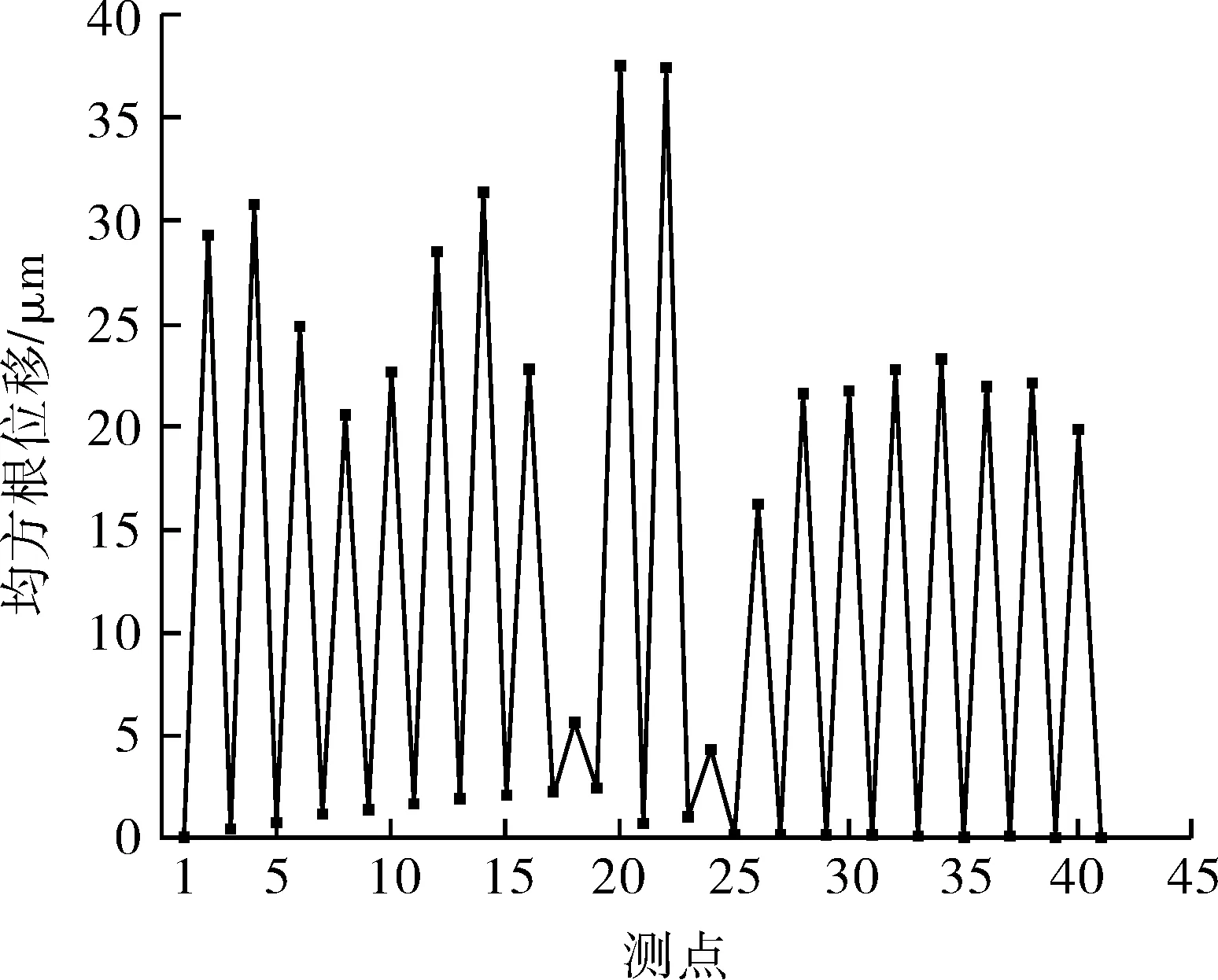
图10 管束测点位置的均方根总位移
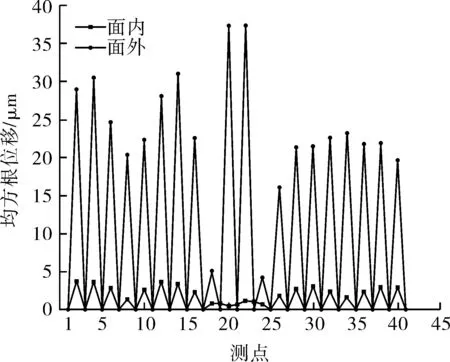
图11 管束测点位置的面内及面外均方根位移
4 结论
本文利用ANSYS CFX软件对发夹式换热器壳侧流场进行了数值模拟,得到了壳侧流体的速度分布;基于流场信息建立U形管的梁单元时域模型,利用ABAQUS软件进行模态分析,并求解随机湍流激振力下管束的位移响应。通过对壳侧流场和管束振动的模拟结果进行分析,得到主要结论如下。
(1)换热器壳侧的直管段内的流体速度变化大,湍流强度高,弯管段内流体速度变化平缓,流场比较均匀。流体高流速区域为直管段的外层管束所在位置,此处的流体湍流强度高,换热能力强,但流体对管束的冲刷强度较大。
(2)本台换热器U形管不同位置处的模态响应差异较大,管束的前4阶模态振型主要为弯管部分的振动,其中第1阶固有频率为77.57 Hz,表现为弯管部分的面内振动;第5和第6阶模态振型分别表现为直管部分的面内和面外振动。
(3)在随机激振力作用下,U形管不同位置处的振动响应也不相同。弯管部位跨度最大的位置均方根位移最大,过渡跨的位移最小。管束的面外位移远大于面内位移。
