工程船穿越航道时间计算模型与应用

张 赫， 刘 昊， 秦鲁莹， 许 程

(大连海事大学交通运输工程学院，大连 116026)

船舶在内河水域实际航行过程中并非一直沿航道行驶，例如汽渡船、施工作业船等船舶会频繁进行穿越航道的操作，而穿越航道过程中穿越船舶会与航道上正常行驶的通航船舶产生交通冲突，甚至导致船舶碰撞事故。因此根据航道通航船舶交通状况为穿越船舶定量计算出合适的穿越时机，可以减小穿越航道过程中的船舶碰撞风险，为目前主要以目测及主观经验判断穿越时机的驾驶员提供更加科学的选择依据，从而提高船舶穿越航道的安全性和可靠性。目前中外对船舶交通冲突方面均有研究，Kumar等[1]提出利用交通冲突技术测量港口水域船舶碰撞危险；王传美等[2]证明了内河交汇水域的环境因素对穿越冲突存在显著影响；程志友等[3]提出了运用综合距离指标测量单船穿越冲突,建立了单船穿越冲突测量模型；何良德等[4]利用改进的可接受间隙理论模型对内河航道交叉口通过能力进行计算，得出通过能力随着冲突交通量的增大成负指数规律减小的结论；程志友等[5]研究了长江干线客渡船横越模型及应用问题，以降低客渡船在穿越主航道过程中与航道船舶流的碰撞风险。

船舶穿越航道时机的计算是建立在通航船舶航行数据信息的基础之上，因此需要获取相关船舶实时准确的航行信息。目前水上交通主要通过传统雷达和船舶自动识别系统(automatic identification system, AIS)两类安全助航设备来提高航行安全及效率，两者均能获得船、物、环境等信息，对AIS与传统雷达各自技术上的优缺点进行融合，可实现各自技术缺陷的互补，进而提高目标识别的准确性和目标跟踪的精度[6]。船舶可通过目前的技术实时准确地获取包括船舶经纬度、船速、航向、航向迹等动态信息，船名、呼号、吃水，船舶尺度及危险货物等静态信息。以工程船穿越内河航道为研究背景，通过预测通航船舶的行驶路径，计算工程船与通航船舶之间的距离，进而帮助工程船选择适合的穿越时机，以在不影响通航船舶正常行驶的前提下使工程船安全地穿越主航道。

1 模型假设及参数确定

1.1 模型假设

(1)船舶航速均为相对于地面的实际航速。

(2)航道实行船舶靠右侧行驶的分道通航规则。

1.2 建立基于航道的直角坐标系

工程船通过船载AIS系统掌握通航船舶的相关静态及动态数据，包括船舶类型、大小、航行速度、航迹向等数据信息，其中船舶航迹向代表船舶在水面上航行的实际轨迹，是预测船舶航迹，计算船舶相遇距离的重要参数，根据通航船舶的航迹向及其他相关航行数据，可对通航船舶的航行状态进行预测，从而计算出工程船的穿越时机。另外目前先进的设施设备已经可以准确获取一定范围内船舶的位置及方位信息，使船舶预测的准确度更加可靠。通过对船舶位置信息的相关数据处理，可以将工程船附近的通航船舶地理位置坐标转换为指定直角坐标[7]，即通航船舶的位置坐标为i(xi,yi)和j(xj,yj)。

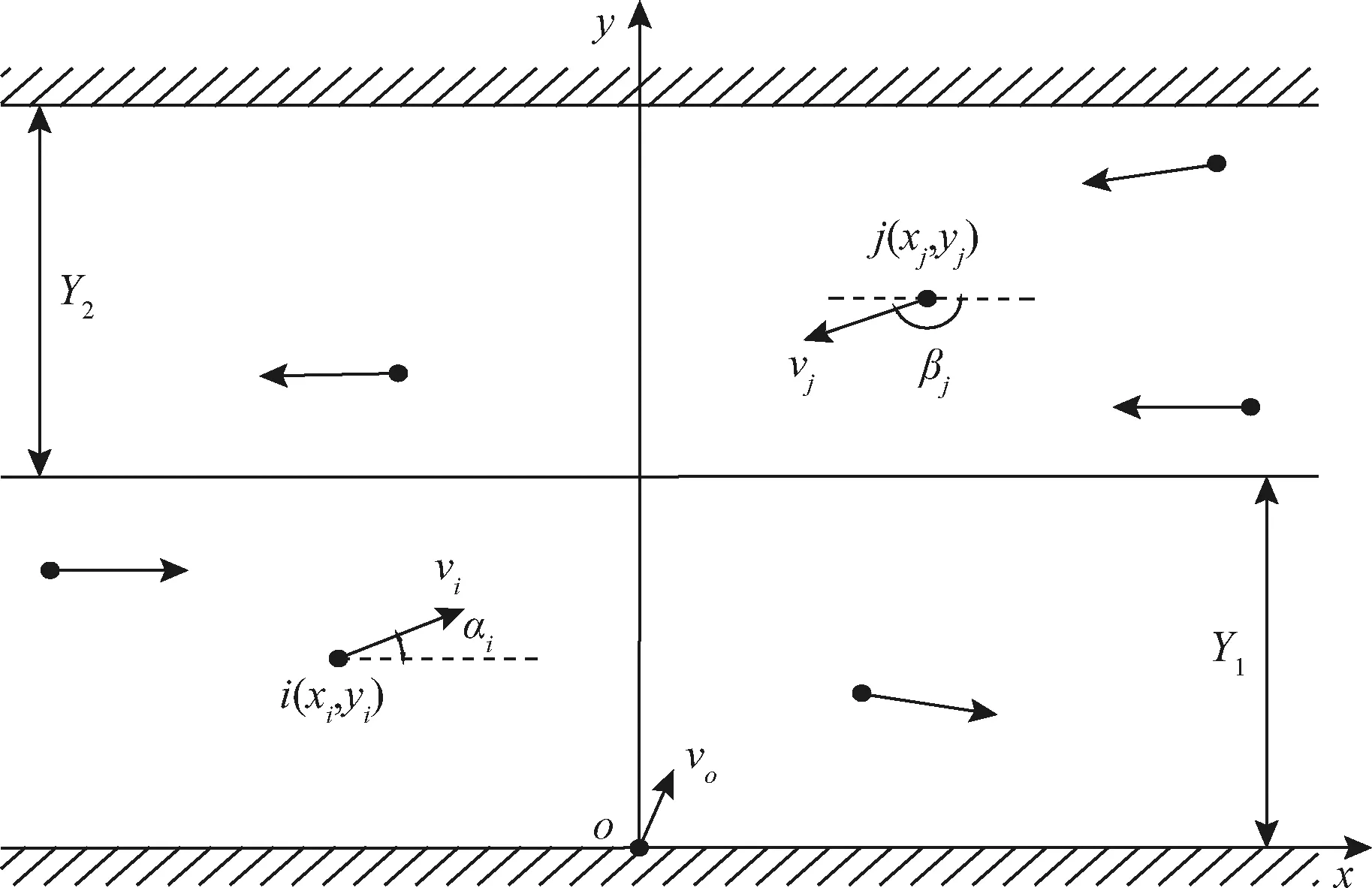
图1 船舶穿越航道示意图Fig.1 Schematic diagram of ship crossing the channel

图1所示为穿越航道示意图。为方便观察，在图1中船舶均以质点(即船舶形心)形式显示在直角坐标系中，建立图中基于航道的直角坐标系，该直角坐标系以工程船穿越起始点为原点，垂直于航道中轴线方向为y轴，航道边线为x轴。其中，工程船穿越航道过程中前半段航道通航船舶的标号为i；vi表示第i艘通航船舶的航行速度；后半段航道通航船舶的标号为j；vj表示第j艘通航船舶的航行速度；Y1表示工程船穿越的前半段航道的宽度；Y2表示工程船穿越的后半段航道的宽度；通航船舶航迹向参数均以x轴正向为基准，逆时针为正，顺时针为负，其中αi表示前半段航道通航船舶i的航迹向与x轴正向之间的角度；βj表示后半段航道通航船舶j的航迹向与x轴正向之间的角度；vo表示工程船穿越航道的速度。

1.3 计算角度参数

这里的角度参数是指不能通过AIS等直接测得，需要根据船舶航迹向等相关数据做进一步计算得出的参数，包括角度αi和βj，其中船舶航迹向是指船舶航迹线的前进方向，由真北线起按顺时针方向至航迹线之间的角度。真北方向是指任意一点沿地球表面朝向地理北极的方向，真北方向不随航道方向、地理位置及地形等的改变而发生变化，因此以真北方向为参考可以计算出所建直角坐标系中通航船舶i与j的航迹向与x轴正向形成的角度αi和βj的大小。

如图2所示为真北方向、船舶航迹向、角度αi和βj参数之间的关系示意图，其中γi表示第i艘通航船舶的航迹向；γj表示第j艘通航船舶的航迹向；γ表示工程船垂直航道穿越时的航迹向，即y轴正向相对于真北方向的角度；θ表示y轴正向沿顺时针方向至工程船实际航迹向的角度；Q表示由真北方向按顺时针方向至x轴正向的角度，另外工程船实际航迹向用γo表示。

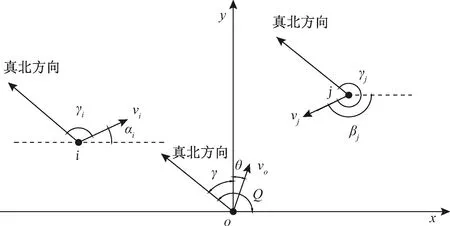
图2 角度参数示意图Fig.2 Angle parameter diagram

首先计算Q的值：

Q=γ+90°

(1)

由于Q的取值范围是(0,360°]，因此

(2)

对于i船而言，其航迹向与x轴正向的角度αi为

αi=Q-γi

(3)

对于j船而言，其航迹向与x轴正向的角度βj为

βj=Q-γj

(4)

工程船实际航迹向与y轴正向的角度θ为

θ=γo-γ

(5)

1.4 船舶最小安全会遇距离

船舶最小安全会遇距离(minimum safe passing distance, MSPD)是指为保证航行安全，两船会遇时应保持的最小安全通过距离，目前航海上确定其值的通常做法是：船舶拥挤水域一般取0.3～0.5 n mile(1 n mile=1.852 km)，大洋航行取1～2 n mile，恶劣天气或能见度不良时取2 n mile以上。该方面研究包括毕修颖等[8]利用模糊神经网络方法给出了最小安全会遇距离的计算公式；刘德新等[9]考虑了各相关因素的影响，建立一个更符合航海实际的最小安全会遇距离决策模型。另外关于船舶安全空间的研究还包括船舶领域的相关内容,船舶领域概念最早由日本学者Fujin等[10]于20世纪60年代初提出,随后由Goodwin等[11]国外学者不断充实和完善。中国学者徐周华等[12]建立了狭窄水域船舶领域三维模型，周丹等[13]研究了船舶领域与其影响因素的关系，并利用神经网络模型对其关系进行建模。

由于目前并没有一个精确可靠的船舶航行最小安全距离的计算公式，因此首先按照航海上的通常做法，取拥挤水域下0.3 n mile和0.5 n mile分别作为船舶最小安全会遇距离对计算结果进行计算分析。

2 模型建立

2.1 船舶距离计算

由于通航船舶航行状态不受工程船影响，因此以前半段航道通航船舶为例(后半段航道通航船舶同理)，其在直角坐标系中的坐标变化为

x′i=xi+vit1cosαi

(6)

y′i=yi+vit1sinαi

(7)

式中，xi和yi分别表示初始时刻第i艘船的横纵坐标；vi表示第i艘船的航速；t1表示从程序运行初始时刻开始计算的时间；αi表示第i艘通航船舶实际航迹与x轴正向的夹角。

工程船在直角坐标系中的初始点为原点，其坐标变化为

x′o=vot2sinθ

(8)

y′o=vot2cosθ

(9)

式中：vo表示工程船的航速；t2表示从工程船穿越时刻开始计算的时间；θ表示工程船实际航迹向与y轴正向之间的角度。

根据式(6)～式(9)可以计算出工程船与通航船舶之间的距离Loi为

(10)

2.2 工程船穿越条件

在拥挤水域中船舶的尺寸大小是不容忽视的参数，而Loi为工程船与通航船舶形心之间的距离，包括了船舶的尺寸，为防控船舶之间产生的交通冲突，避免船舶碰撞风险，船舶在航行过程中除去船舶尺寸大小外还应保持额外的最小安全距离。即:

(11)

式(11)中：Lo表示工程船的船长；Li表示通航船舶i的船长；S表示船舶之间应保持的最小安全距离。

3 模型应用

利用MATLAB软件为工具，对以上模型进行编程，为方便直观地查看所得结果的具体穿越时间段，利用MATLAB导出当前时间以及可穿越时间段的起止时间。

其基本思路是工程船通过相关设施设备获取一定区域的通航船舶的实时航行信息，假设所有通航船舶以当前所获取的实时航行状态持续航行，则其航行轨迹为可预测值，每一时刻通航船舶的位置也可以通过计算得出，利用MATLAB编程结合所建立的模型，以1 s为间隔计算指定时间段(设为600 s)内工程船是否可以安全穿越航道，如果可以则记录该时刻，将该时刻信息储存直至得到船舶不能穿越的时刻或计算终止时刻，最后将起止时间输出至矩阵中保存，待将指定时间段内所有时刻计算完毕之后将最终结果输出，最终可得出工程船能够安全穿越航道的时间段。

4 案例

4.1 计算流程

通过MATLAB，按图3所示的流程进行编程。

4.2 案例计算

假设以某一工程船为例，其穿越航道所需相关数据分别为：主航道前半段宽度为Y1=575 m；后半段航道宽度为Y2=584 m；工程船航速为6 kn(1 kn=1 n mile/h)，船长52 m，当船舶垂直穿越航道时其航迹向为6.8°；航道上行驶的通航船舶的相关数据信息如表1所示。

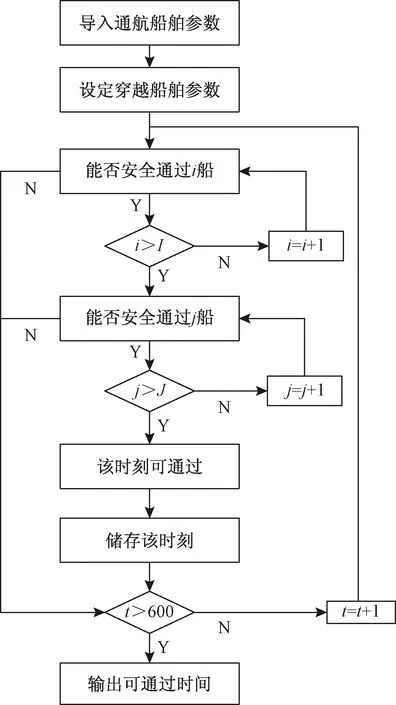
图3 穿越时间计算流程图Fig.3 Crossing time calculation flow chart

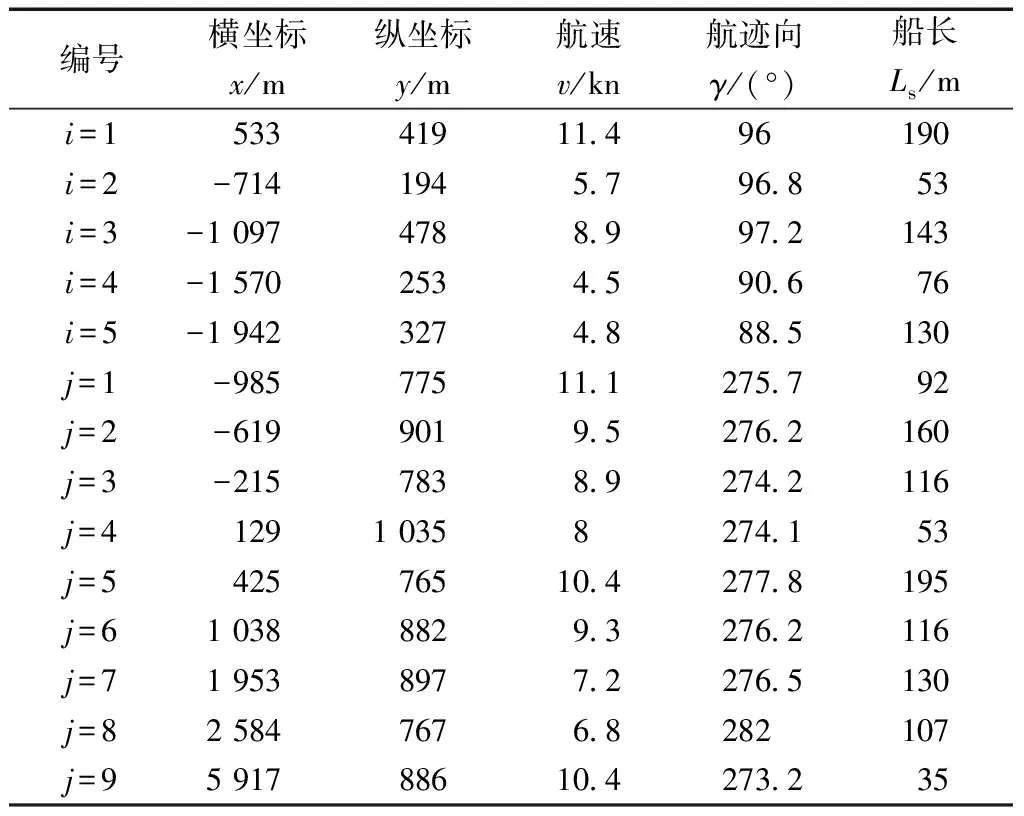
表1 通航船舶相关参数Table 1 Navigational ship parameters

依据工程船穿越时机的计算模型及流程，利用MATLAB软件对该模型进行编程，通过将获取得到的通航船舶的相关数据以及工程船航行数据导入程序，计算工程船可安全穿越航道的时机，计算结果分别以时分秒时间段和总秒数时间段显示。

假设工程船以垂直主航道的角度进行穿越，由表1中通航船舶信息可以看出，当前时刻航道上的通航船舶属于非常密集的状态，将表1数据导入，通过MATLAB程序运行结果显示，若将最小安全距离设定为航海船舶拥挤水域下的0.3～0.5 n mile时，工程船在未来600 s时间内可穿越航道的时间段不存在，因此内河拥挤水域船舶最小安全会遇距离应根据实际需要适当减小，例如本例中若将该距离缩小为100 m，则程序运行结果显示工程船可在7～10 s和321～343 s两个时间段内安全穿越航道。

4.3 结果分析

影响工程船穿越时间段的因素除最小安全会遇距离的大小外，还与工程船穿越速度、角度以及主航道交通流量有关。以案例程序为基础，可以进一步得出工程船可穿越时间与其影响因素之间的关系，如图4～图7所示。

图4表示工程船以垂直于航道的角度穿越且最小安全会遇距离设定为100 m条件下，可穿越航道的总时间与工程船航速之间的关系。由于要在600 s内工程船完成穿越航道该程序才有意义，因此工程船速度至少为3.8 kn，其航速最大值设定为15 kn。由图4可以看出随工程船穿越速度的增加可穿越时间先减小后增大，这是由于当工程船以较低的速度航行时，其穿越航道所需的时间也会增加，这会使其在穿越航道过程中会与更多的通航船舶产生交通冲突。

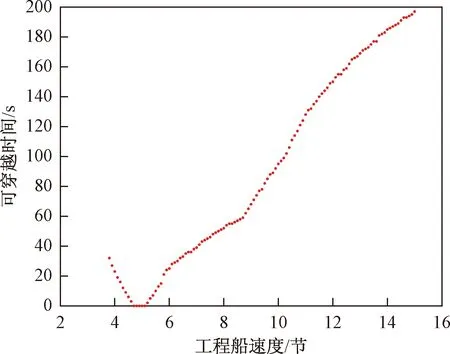
图4 穿越速度的影响Fig.4 Impact of crossing speed

图5表示工程船以6 kn航速穿越航道且最小安全会遇距离设定为100 m时，可穿越航道的总时间与工程船穿越角度之间的关系。由于要在600 s内工程船完成穿越航道，因此工程船穿越角度最多为51.2°。工程船在穿越时可依据该关系选择出当前船舶交通环境下的穿越角度，以保证工程船有足够的穿越时间可供选择。

图6表示工程船以6 kn航速垂直穿越航道时，可穿越航道的总时间与船舶最小安全会遇距离之间的关系。由图6可知由于当前船舶流量较大，可穿越时间随最小安全会遇距离的增大而快速减小，当最小安全会遇距离为126 m及以上时，以当前航道交通流情况，工程船在未来600 s时间内将无法穿越航道。而当航道船舶交通流量较小时，可穿越航道的最小安全会遇距离范围会相应增加，假设当前交通流只包含i=1,5和j=2,4,6共五艘船舶，则结果如图7所示。最小安全会遇距离并非随意设置，在不同航行环境下，船舶最小安全会遇距离也存在差异，船舶驾驶员可根据实际情况适当设置该距离值的大小，但为了保证船舶航行安全，不能为了扩大可穿越时间的范围而过多减小最小安全距离。

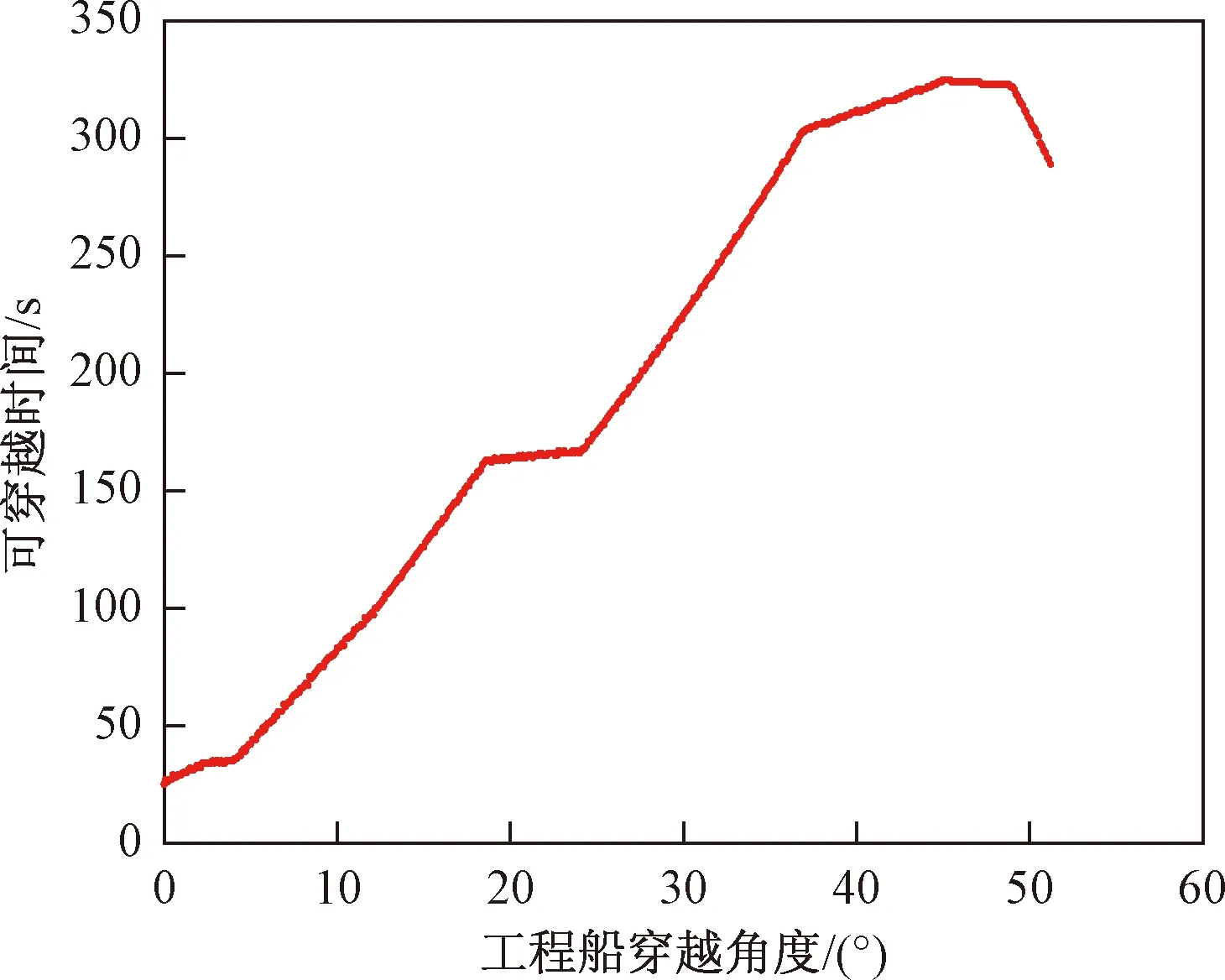
图5 穿越角度的影响Fig.5 Impact of crossing angle

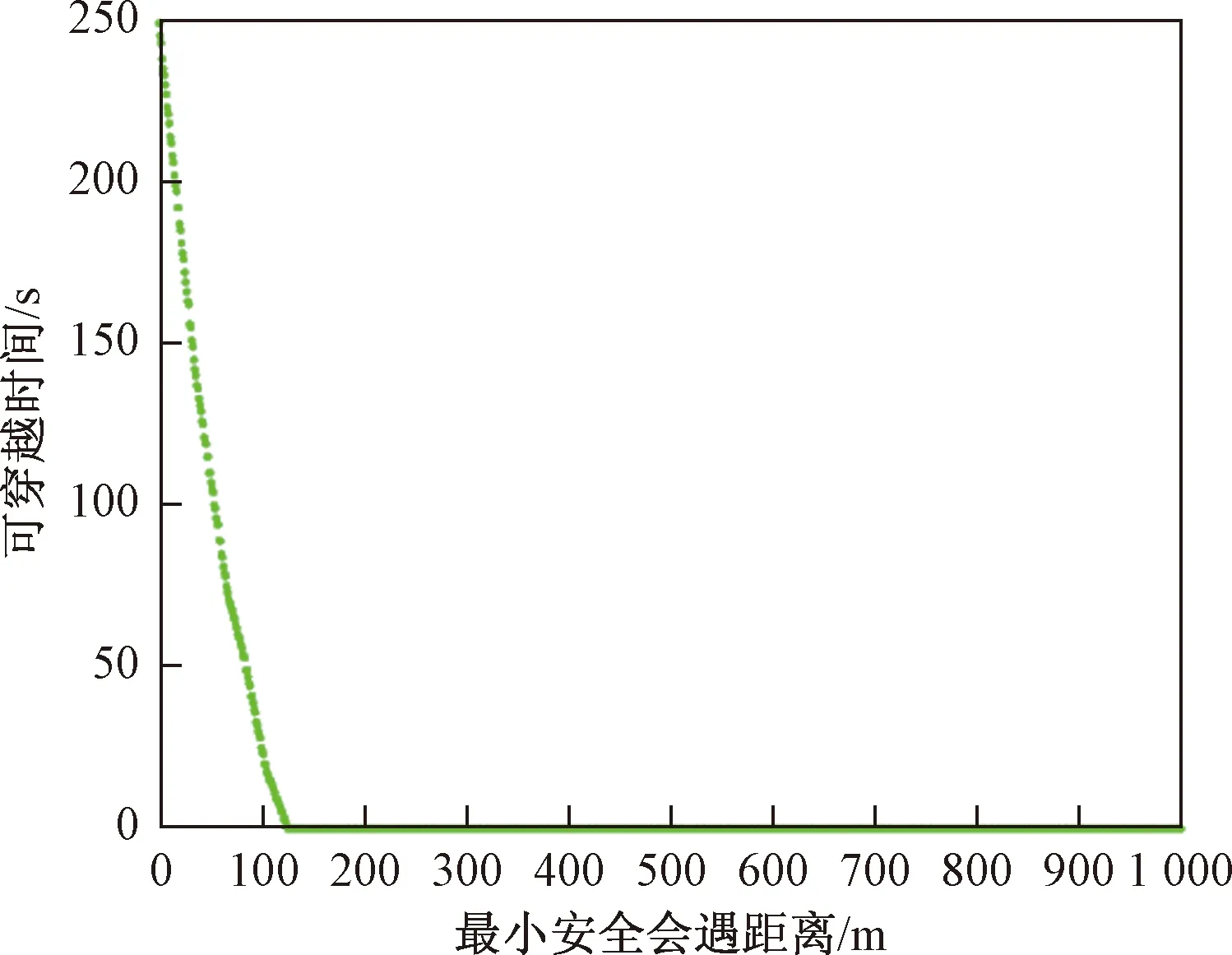
图6 较大船舶流下MSPD的影响Fig.6 The impact of MSPD on larger ships

图7 较小船舶流下MSPD的影响Fig.7 The impact of MSPD on smaller ships

5 结论

主要针对工程船进行穿越主航道操作时，根据实际航行环境为工程船计算出合理的穿越时间段，帮助驾驶员选择合适的穿越时机，提高工程船穿越主航道的安全性和可靠性。模型及程序的运行依赖于相关设施设备的支持，对所获取的船舶航行信息的准确性和时效性要求较高。当程序计算的可穿越时间段范围较小，不利于工程船选择合适的穿越时机时，驾驶员可通过调整穿越点位置、改变工程船航速、选择穿越航道角度、设定合适的最小安全会遇距离等方法重新计算结果，以保证得到的计算结果的可穿越时间段范围足够大，船舶穿越时机的选择足够多，从而使船舶穿越更加安全。

程序是以当前导入的静态船舶航行信息为计算依据，而实际各通航船舶的航行信息是不断变化的，因此程序所预测的结果随时间的增加，误差会逐渐增大，为避免较大误差，程序需要以一定时间间隔重复运行，且每次运行都应更新船舶的实时信息，保证导入程序中数据的时效性，从而提高预测的准确度。

该模型程序主要应用于航道船舶流量较大，不易通过人为目测等主观方式确定穿越时机的情况，所计算结果可作为驾驶员选择穿越时机的参考依据，但船舶驾驶员仍需在船舶穿越过程中保持正规瞭望，使用雷达、VHF、AIS等方法，对穿越船舶周围的航行环境进行全方位的系统监视和观察。