箱梁预应力管道内空洞探地雷达有限元正演模拟
2020-04-22舒志乐黄柳婷吴林龙
舒志乐, 赵 柳, 黄柳婷, 吴林龙, 李 亨
(1.西华大学土木建筑与环境学院,成都 610039;2.四川省建筑设计研究院,成都 610000;3.丹棱县住房和城乡规划建设局,眉山 620200)
中国交通运输基础设施发展迅速,目前已建成公路桥梁超80×104座,其中预应力混凝土箱梁在桥梁建设中应用广泛。但预应力管道注浆缺陷导致预应力筋锈蚀及有效应力降低,不仅影响桥梁的正常使用寿命,甚至直接威胁到结构的安全性能[1-2]。因此,在建设过程中必须加强桥梁预应力管道内注浆质量检测,以保证桥梁的安全性和耐久性。
探地雷达(ground penetrating radar,GPR)作为一种快速、无损、高效的检测方法,在工程领域得到了广泛的应用与研究[3-6]。在应用探地雷达检测桥梁预应力管道病害方面,许多学者进行了大量研究:辛公峰等[7]通过室内试验和现场检测,验证了探地雷达用于检测塑料波纹管内部压浆缺陷时有着较高的分辨率,但无法应用于对金属波纹管的探测;潘海结[8]利用HIRESS天线阵探地雷达对桥T梁预应力波纹管进行了压浆密实性检测,表明注浆密实管道雷达图像呈单振相特征,注浆有缺陷的半空管道呈双振相;化得钧等[9]对钢绞线注浆孔道中埋深相同大小不同的空洞进行基于时域有限差分法二维正演,得出空洞越大,圆弧形同相轴开口越大的结论;杜良等[10]通过数值模拟和现场试验验证了利用探地雷达2.6 GHz天线可以检测到11 cm预应力混凝土板中塑料波纹管注浆情况。目前对公路桥梁的检测技术不断发展[11-12],但在应用探地雷达对箱梁预应力管道内空洞进行三维探测及数值模拟方面的研究还不够成熟。本文制作了箱梁预应力管道内不同空洞病害模型,用Randa7软件对雷达图像进行优化处理并分析其成像特点;将有限元法(finite element method,FEM)应用到探地雷达电磁波的数值分析研究中,并用改进Sarma吸收边界对预应力管道内空洞进行正演模拟。验证了雷达探测方法及数值模拟方法的可靠性,对箱梁质量检测、评定及加固工程具有重要指导意义。
1 箱梁预应力管道内空洞模型试验
1.1 物理模型制作及测线布置
按照公路桥箱梁结构以1∶1的比例设计试验模型,尺寸及顶板预应力管道布置示意图如图1。由于金属对电磁波信号具有屏蔽作用,试验中采用长1 000 mm、直径160 mm的塑料PVC管来代替金属波纹管。
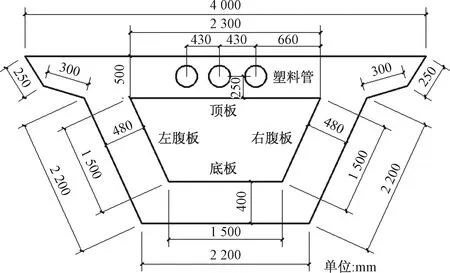
图1 箱梁尺寸及顶板预应力管道布置示意图Fig.1 Size of box girder and layout diagram of prestressed pipe on roof
箱梁模型采用钢筋混凝土结构,混凝土级别为C30,水泥级别为32.5R,采用标准砂石,混凝土每立方米配合比为砂∶石∶水泥∶水=680∶1 260∶300∶160 (kg),模型顶板的纵横向钢筋间距为40 cm。在模型顶板处从左往右布设3个PVC管2种不同的病害,分别为注浆密实、部分注浆、空洞充水。管道内部采用TH-303孔道压浆料,充水空洞采用长100 mm、直径为75 mm的圆柱PVC管,箱梁顶板病害布置示意图如图2。

图2 箱梁顶板病害布置示意图Fig.2 Schematic diagram of the disease arrangement of box girder roof
使用剖面法进行探测,测线间距应综合考虑介质体的最小尺寸、天线中心频率、精度要求等[13-14]。采用间距为2.5 cm的方格网,探测范围137.5 cm×67.5 cm,如图3所示。其中水平方向为X轴,探测方向为从左到右,从上到下,竖直方向为Y轴,探测方向为从上到下,从左到右。

图3 坐标系及测线布置Fig.3 Coordinate system and survey line layout
1.2 探地雷达参数设置
通过SIR-3000型探地雷达对目标体进行探测,采集图像并进行分析、解释。考虑到箱梁预应力板最厚处只有0.5 m,且对目标体在精度方面要求比较高,选取1 600 MHz的天线进行检测。
雷达参数设置:采样点数为512个,记录长度为15 ns;混凝土介电常数ε一般在4~10之间,考虑到试验模型的不均匀性,选取目标ε为9,电导率σ为0.001~0.1 S/m,空气的ε为1,σ为0,水的ε为81,σ为0.15 S/m;扫描速度为120个/s,扫描单位为400个/m,IIR低通滤波设置为2 500,IIR高通滤波设置为225,采用3次叠加。
1.3 试验数据的处理与分析
选用X方向第10道测线的灰度图像作为分析依据,如图4。在深度为0~0.1 m区间有间距均匀大小相等的“抛物线”形图像,根据实际情况分析,顶板内部钢筋间距为40 cm,故此处为钢筋的探地雷达图像。由图像可以看出黑框标记①处无异常信号,为注浆饱满的PVC管;标记②处有“弧形”异常信号,为一半注浆一半空洞的预应力PVC管;标记③处有同相轴错乱的“弧形”异常信号反应,为空洞充水预应力PVC管道。在该图像中,钢筋和空洞的水平位置是基本符合当初的设计要求,深度与设计有一定的出入,主要是由于雷达天线不能与模型表面完全贴合,导致顶部有一段多余的深度。
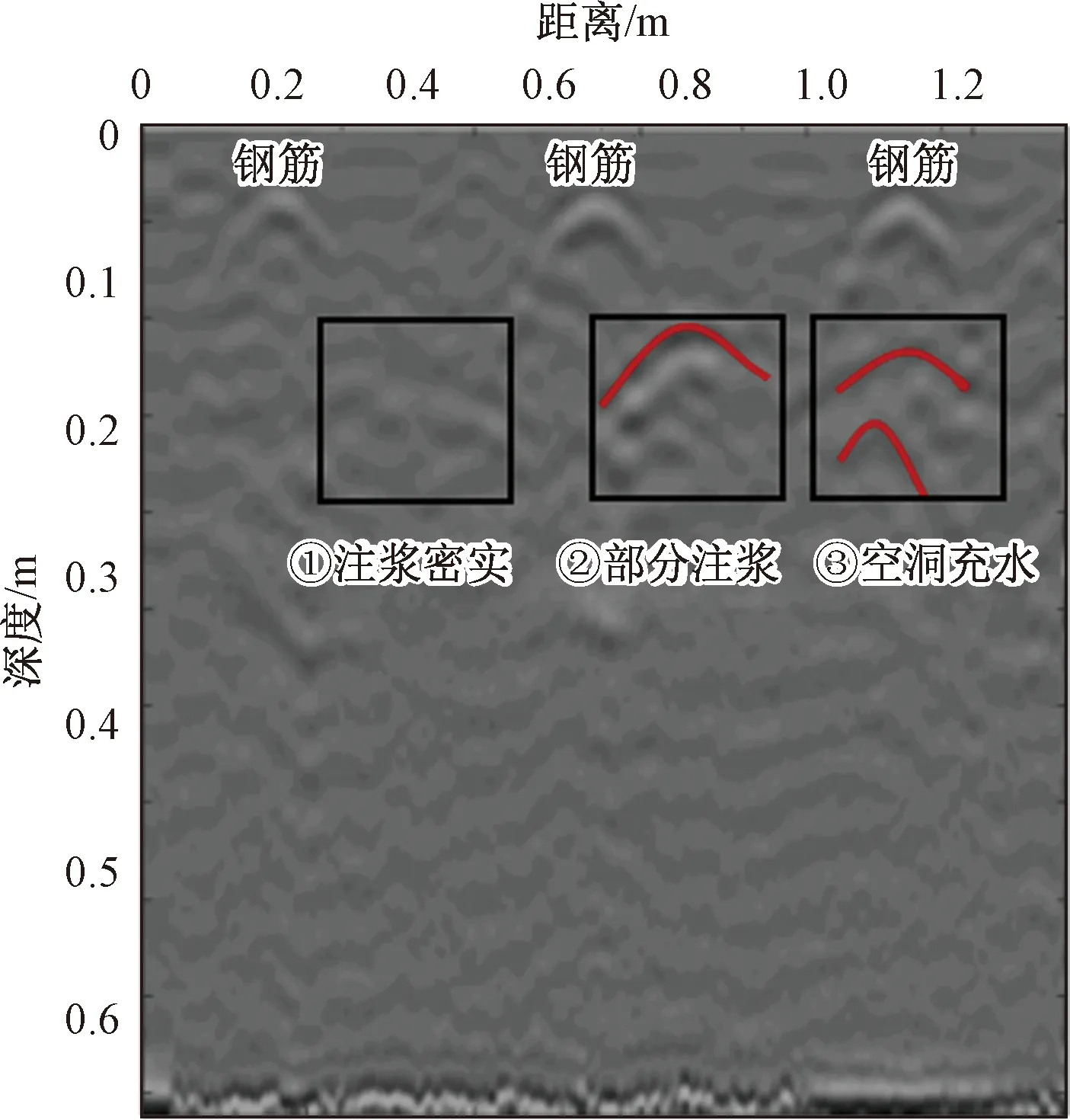
图4 二维剖面Fig.4 Two-dimensional profile
图5为不同深度的三维切片病害图像,图5中黄绿色部分为钢筋及病害信号反应。从Z=3.75 cm开始,出现了三道间距约为40 cm、分布均匀的强烈信号,且此信号在Z=11.99 cm处彻底消失。根据模型设计及图4中钢筋反射信号在10 cm左右基本消失,可判断此处为钢筋的信号反应。在Z=15.74 cm、X方向0.7~0.9 m处出现了异常信号,根据图像位置可判断此处为部分注浆病害。在Z=19.44 cm处,除部分注浆病害的反射信号外,在X方向1.0~1.3 m处还出现了充水空洞病害的反射信号。由于水的介电常数远大于空气的介电常数,电磁波在水中的传播速度小于其在空气中的传播速度,所以部分注浆病害信号早于充水空洞病害信号出现。此外,除病害布置处,图5中还出现了少数零星的异常信号,是由于模型局部位置出现浇筑不密实导致。

图5 不同深度三维切片图Fig.5 Three-dimensional slice map with different depth
2 GPR波动方程
从Maxwell旋度方程出发,无源条件下,推导出电磁波在地下介质中传播的表达式为[15]
(1)
(2)
假设等效磁场源SH和等效电场源SE,将雷达波激励源代入式(1)、式(2),推导出探地雷达的波动方程为
(3)
(4)
式中:E为电场强度,V/m;H为磁场强度,A/m;σ为电导率,S/m;ε为介电常数,F/m;μ为磁导率,H/m。
从式(3)、式(4)可以看出,磁场和电场及其相应的分量满足相同的微分方程。
3 有限元法在GPR波动方程中的应用
3.1 探地雷达有限元方程
有限元法是比较近似和高效的数值计算方法,其求解思想是将空间划分成一系列的有限个单元,并对其中的每个单元选用插值函数,以近似地表示场函数在单元内的局部特征。用伽辽金法来推导GPR有限元方程,可以得到GPR的二维有限元的波动方程[16],即式(3)、式(4)可换为
(5)
(6)

3.2 改进Sarma吸收边界加载
Sarma吸收边界是在求解区域外加载一定厚度的衰减层,这个衰减层可由阻尼矩阵来实现。由Caughey[17]提出的阻尼矩阵计算方法,通过整体刚度矩阵K和整体质量矩阵M可得出阻尼矩阵F:
F=a0M+a1K
(7)
(8)
(9)
式中:a0、a1表示比例系数;ωi和ωj是目标体场源的第i和j个固有的圆频率;ξ是对应的阻尼比,一般取值范围在[0.05,0.30]区间内。
ξ与a0、a1两个比例系数的关系如下:
(10)
由于恒定的比例系数会导致衰减层与介质之间出现明显的物性差异而发生反射,王月英等[18]提出一种改进的Sarma边界条件:在模型介质与衰减层之间加设一层过渡带,在过渡带内设置从零逐渐增大的比例系数ai,以达到用有限空间模拟无限空间中电磁波传播状态的目的:
(11)
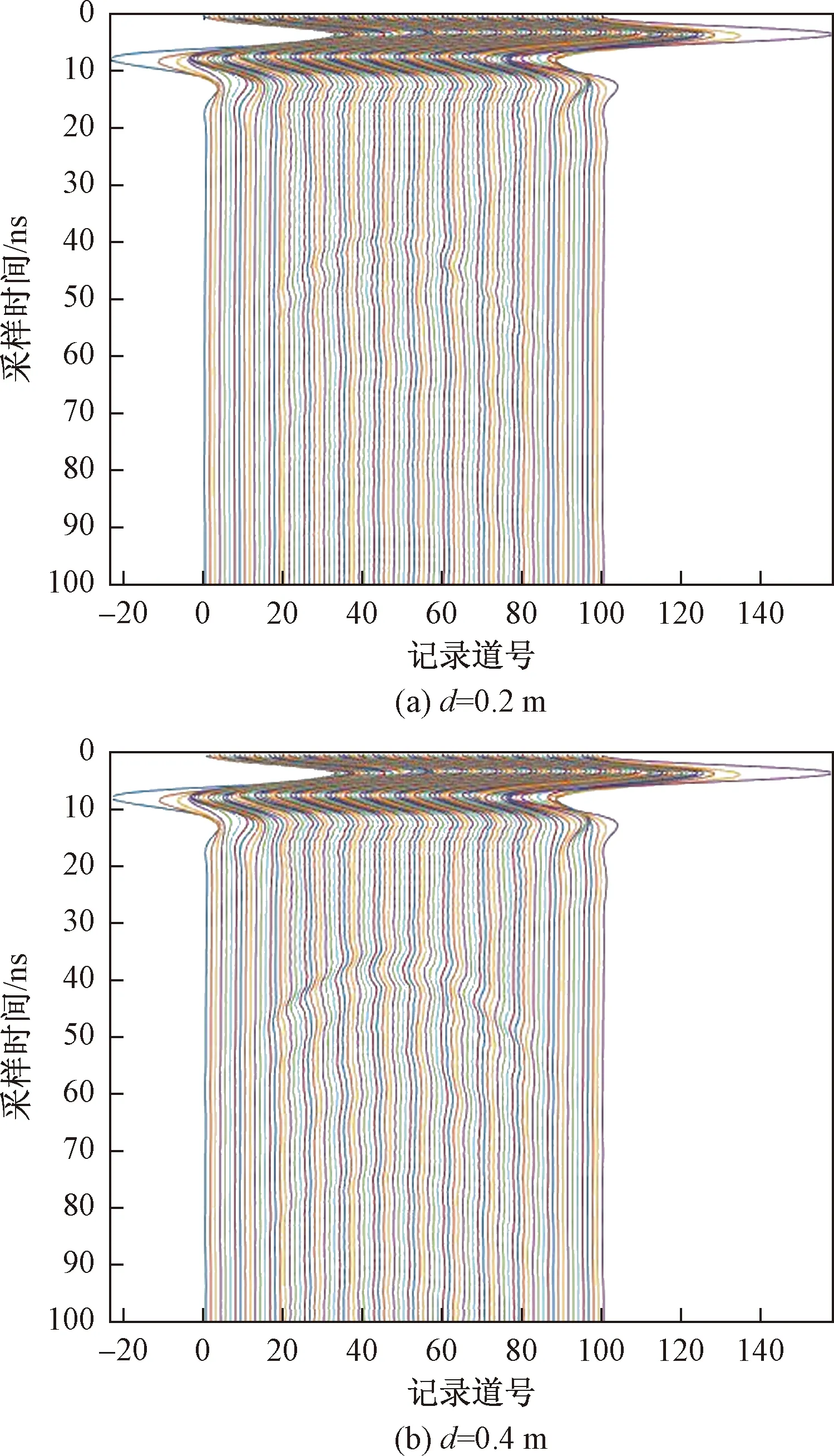
在模型中设衰减层和过渡带分别有n、m个网格(m 将改进Sarma吸收边界融入探地雷达有限元法得到方程[16]: (12) 将式(5)与式(12)结合进行探地雷达有限元正演模拟。 模型尺寸为10.00 m×5.00 m,模拟箱梁预应力管道内的空洞病害,如图6。空洞直径分别设置为d=0.2 m、d=0.4 m,中心点位于整个模型的中心。背景网格设置为100×50个,间距大小为0.1 m×0.1 m。混凝土的电导率为0.005 S/m,相对介电常数为9,空洞内介质相对介电常数为1,高斯积分的阶数取4阶。探地雷达波脉冲激励源的中心频率为100 MHz,时间步长为0.25×10-9s,计算时窗长度为100×10-9s。 图6 空洞模型图Fig.6 Hole model diagram 图7 不同大小空洞正演模拟剖面曲线Fig.7 Forward modeling section curves of different size cavities 应用基于改进Sarma吸收边界的有限元法对该模型进行正演模拟,所得的探地雷达正演模拟剖面曲线图如图7,图7中滤去了0~15 ns范围内在模型介质界面处直达波的强反射。由图7可见,在模型边界处,由于设置了衰减层,探地雷达电磁波产生的能量大部分被吸收,模型左、右、底边界的反射波非常弱。图7(a)40 ns处与图7(b)35 ns处“抛物线”形状的波为空洞处的反射波信号,从波峰到波的两端逐渐减弱,与模型试验中所测得空洞信号一致。对比图7(a)、图7(b)可知:①空洞回波信号出现的时间、回波强度均与其几何尺寸有关,在中心埋深相同的情况下,尺寸较小的空洞上层界面埋深较大,回波延时较长,回波双曲线出现的时间较晚,回波强度较小;②空洞规模越大,双曲线延长度越大,曲率越大;③在回波双曲线中,最上方和最下方曲线之间的距离与空洞尺寸有关,尺寸越大,回波双曲线间距越大,且由于电磁波在传播过程中不断衰减,空洞下界面反射波能量比上界面弱。 图8为探地雷达正演模拟三维剖面图,更加明显地反映出探地雷达探测实际模型的电磁波信号情况。由图8可知,目标体的反射信号及介质的传播情况都与实际试验的探测结果相吻合。 图8 不同大小空洞正演模拟三维剖面图Fig.8 Forward modeling of three-dimensional section curves of different size cavities 通过利用探地雷达对箱梁预应力管道内空洞进行物理模型试验及正演模拟,可以得出以下结论。 (1)探地雷达检测法能有效地识别箱梁内钢筋的位置及分布,直观地反映出预应力管道内不同空洞病害的信号特征。 (2)数值模拟结果表明:当空洞中心埋深相同时,尺寸越小,回波延时越长,回波强度越小,双曲线延长度越小,曲率越小。 (3)将MATLAB软件模拟结果与物理模型探测结果进行对比分析,空洞在结果图上均出现“弧线”形态强反射,且能确定空洞的位置和埋深,表明数值模拟是适用的,为实际工程中不同类型病害的图像提供了解释依据。4 探地雷达正演模拟实例


5 结论
