考虑渗透系数变异性的堤防渗透破坏概率分析方法
2020-04-22柯浩进
柯浩进, 王 媛, 冯 迪
(河海大学岩土力学与堤坝工程教育部国家重点实验室,土木与交通学院隧道与城市轨道工程研究所, 南京 210098)
洪水是威胁中国人民生命财产安全的重要自然灾害之一,堤防工程作为抵御洪水的一道安全屏障,其渗流稳定性尤为重要。然而中国的堤防流域广、年代久,堤防本身的地质条件存在较大的差异,且经过历史变迁,同一河段堤身填筑材料也不一致,以上诸多随机因素造成了堤防土体渗透系数具有一定的变异性,对堤防渗流场有着重要影响[1-4]。由于以往确定性方法无法表征随机因素对堤防渗流场的影响,以可靠度理论为基础的概率分析方法被广泛应用到堤防工程中来。李锦辉等[5]基于摄动随机有限元法研究了水位变化、堤顶宽度等因素与堤防渗透失稳概率的关系。王靖文等[6]将故障树和蒙特卡洛法结合起来建立了求解堤防渗透失稳概率的方法。王亚军等[7]基于蒙特卡洛法和first order reliability method理论建立了堤防系统广义模糊可靠度算法,分析了堤防不同失效模式下的失效概率。焦小超[8]以水头和土体的物理力学参数作为随机变量,计算了堤防管涌破坏极限状态方程。张秀勇等[9]结合有限元方法与蒙特卡洛法,采用堤防单元土体有效土重力与土体底部的渗透力之差作为极限状态方程,方程中忽略了土体黏聚力及摩擦力的影响,使得结果偏保守。邢万波等[10]针对流土、管涌建立了不同失效模式下的极限状态方程,但却仅限于堤基部分,不能用于堤身的渗透破坏计算。高昂等[11]、雷鹏等[12]在有限元方法的基础上,将神经网络、拉丁超立方抽样等方法与有限元方法相结合,但却未能将土体参数的变异性考虑到有限元模型中去,无法考虑水力梯度的不确定性。
基于以上背景,将渗透系数视为随机变量,与有限元软件Abaqus相结合,结合蒙特卡洛法分析了渗透系数变异性对堤防渗流场的影响。基于不同破坏区域,将水力梯度、土体黏聚力、摩擦角等因素作为随机变量,建立了堤防渗流破坏极限状态方程,并结合改进的验算点法(JC法)实现堤防工程渗流破坏概率分析。
1 堤防随机渗流场分析
1.1 堤防随机渗流分析方法
渗透系数的不确定性对堤防渗流场内各区域水力梯度有一定的影响,为此采取将渗透系数视为随机变量的方法,与有限元方法相结合,分析渗透系数不同变异性下的堤防渗流场情况。利用有限元软件Abaqus进行建模并划分网格,针对划分好的单元网格,基于Python语言编写渗透系数随机赋值的脚本,通过脚本读取模型的每一个网格单元,对应每一个单元设置一个截面,同时随机生成一个满足要求的材料,并将该材料赋给截面,通过遍历循环从而建立一个堤防随机渗流模型。具体如图1所示。

图1 随机有限元方法流程图Fig.1 Stochastic finite element method flow chart
1.2 有限元模型建立
选取某一典型堤防断面,模型参考Lam坝体有限元渗流分析[13],模型如图2所示,以堤基为基准面,堤身高度为12 m,堤顶长度为4 m,两侧坡比均为1∶2,上游水位设置为10 m,下游水位为2 m,渗透系数均值设置为1×10-7cm/s,标准差为2×10-8,据上述内容建立有限元模型,单元划分结果如图2所示,共1 052个节点,971个单元。
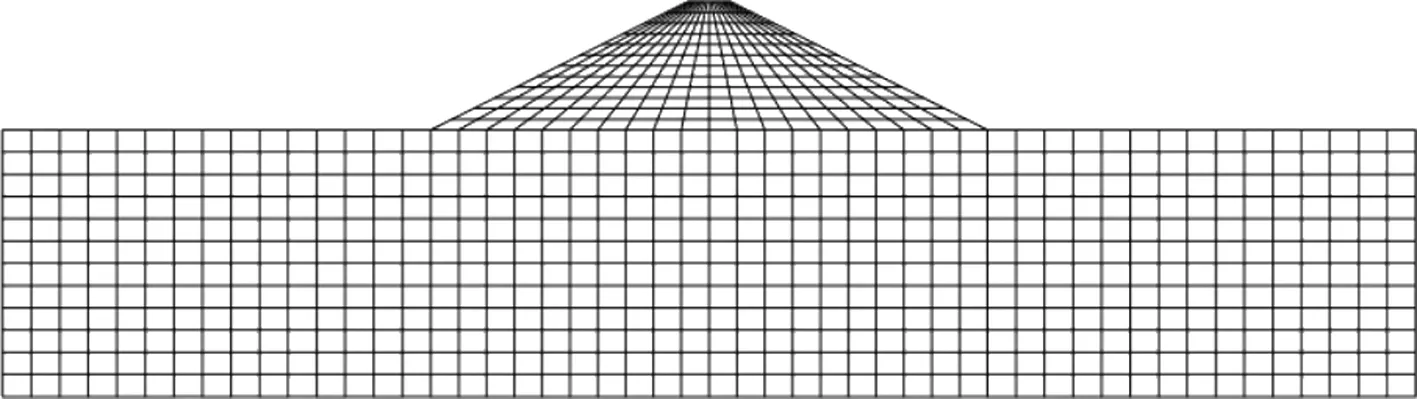
图2 堤防模型网格单元Fig.2 Levee model mesh units
1.3 渗透系数变异性对堤防渗流场的影响分析
将上述有限元模型渗透系数均值设定为1×10-7cm/s,变异系数分别设置为0.2、0.4、0.6来进行计算。取1 000次计算进行结果统计并使用Tecplot绘制云图。绘制了不同变异系数条件下的水头均值图[图3(a)]和标准差图(图4)以及水力梯度均值图[图3(b)]和标准差图(图5),将各云图进行比较分析发现,不同变异性条件下,渗流场的水头和水力梯度均值无明显波动。
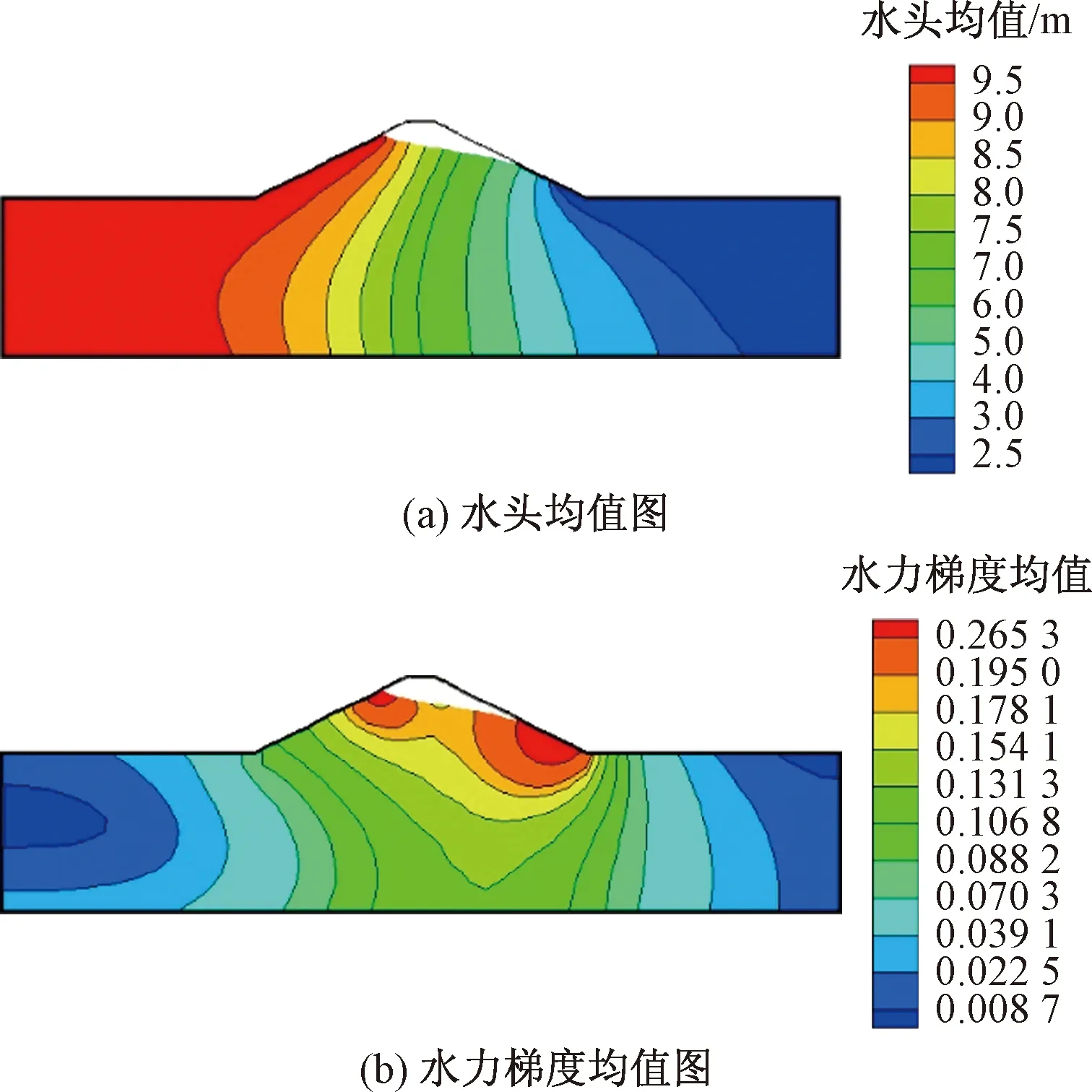
图3 均值等值线图Fig.3 Mean isogram map
变异系数的改变对渗流场的均值无明显影响,在变异性较小的情况下,非均质土体渗流场与均质土体渗流场较为接近。

图4 不同变异系数的水头标准差图Fig.4 Standard deviation map of water head with different coefficient of variation
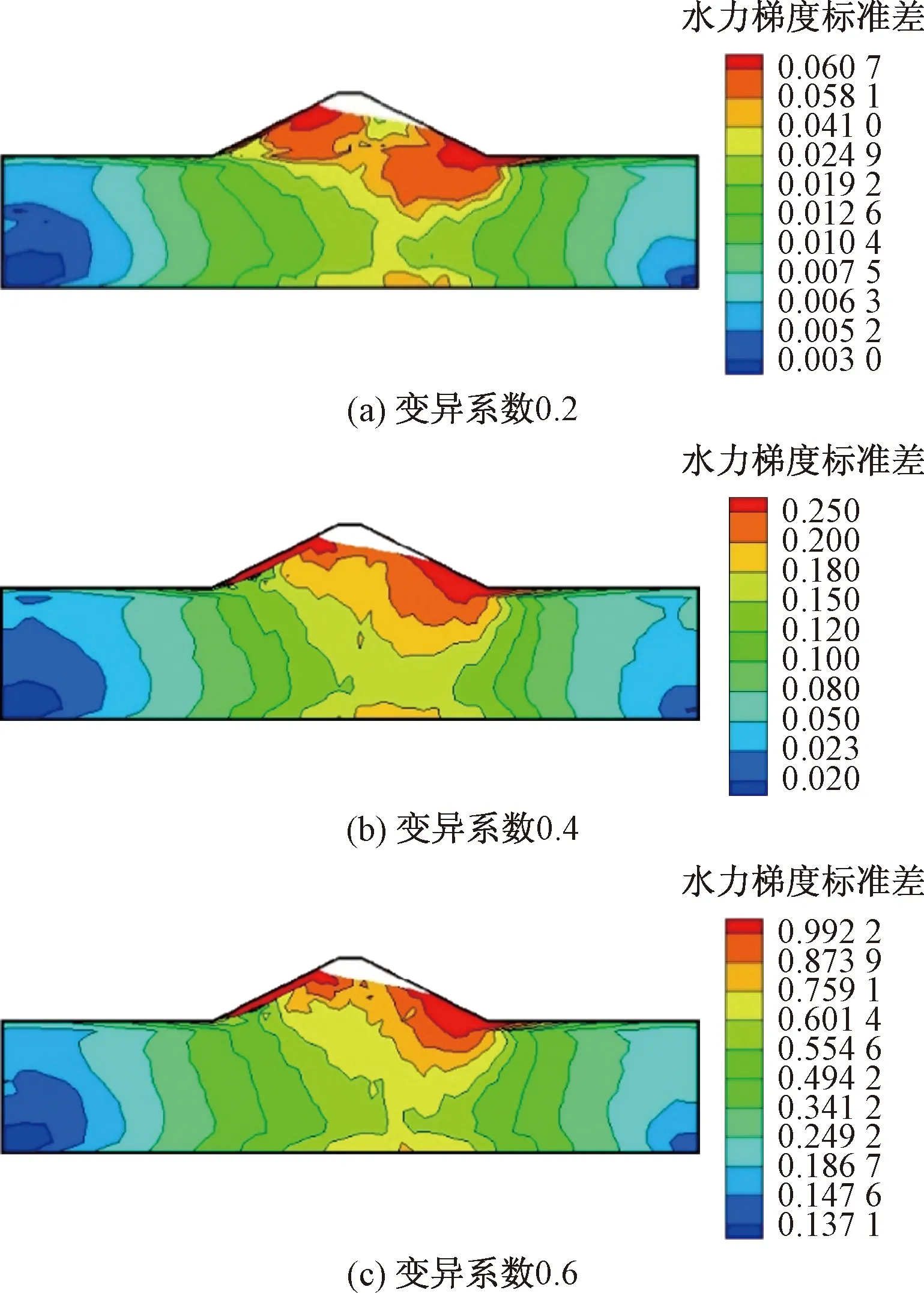
图5 不同变异系数条件下的水力梯度标准差云图Fig.5 Standard deviation map of hydraulic gradient under different coefficient of variation
从图4对比可以看出,在稳定渗流条件下,堤防水位以下的边界位置标准差较小,这是因为稳定渗流时,边界水头是确定的,所以标准差较小。标准差较大的位置出现在堤防背水坡逸出点附近。变异系数的变化对标准差的分布形式无明显影响,但变异系数的增大使堤防各区域水头的标准差变大。
从图5对比可以看出,变异系数的增大使得各区域水力梯度标准差变大,变异系数的变化对水力梯度标准差的分布形式无明显影响。水力梯度标准差在堤防边界处较大,堤身内部较小,这就意味着在堤防边界处水力梯度波动幅度较大,而边界处正是堤防发生破坏开始的位置,所以研究此处堤防破坏的概率是有必要的。
2 基于JC法的堤防渗流失稳可靠性分析
2.1 JC法基本原理
工程中在进行结构可靠度分析时,常常会有多个因素同时影响着结构整体的稳定性,所以构造出的结构极限状态方程往往也包含多个变量:
Z=g(X)=0
(1)
JC法实质是改进的验算点法,取极限状态面上的一点x*,并在该点按泰勒级数展开保留至一次项:
(2)
在随机变量空间X里,方程ZL=0 为过该点的极限状态面的切平面。假设X服从正态分布,利用相互独立正态分布的随机变量线性组合的性质,ZL的均值和标准差为
(3)
(4)
则有:
(5)
定义一个灵敏系数axi,令:
(6)
经过标准化处理可得到:
(7)
(8)
(9)
JC法计算可靠度的步骤是先假定一个初始的验算点,然后检验随机变量是否服从正态分布,如果不服从,则进行当量正态化计算,将经过当量正态化转换后的均值和标准差代入计算,得到新的验算点坐标,并重复上述步骤进行迭代计算,通过比较前后两验算点坐标之差是否小于允许值来终止计算,计算流程图如图6所示。
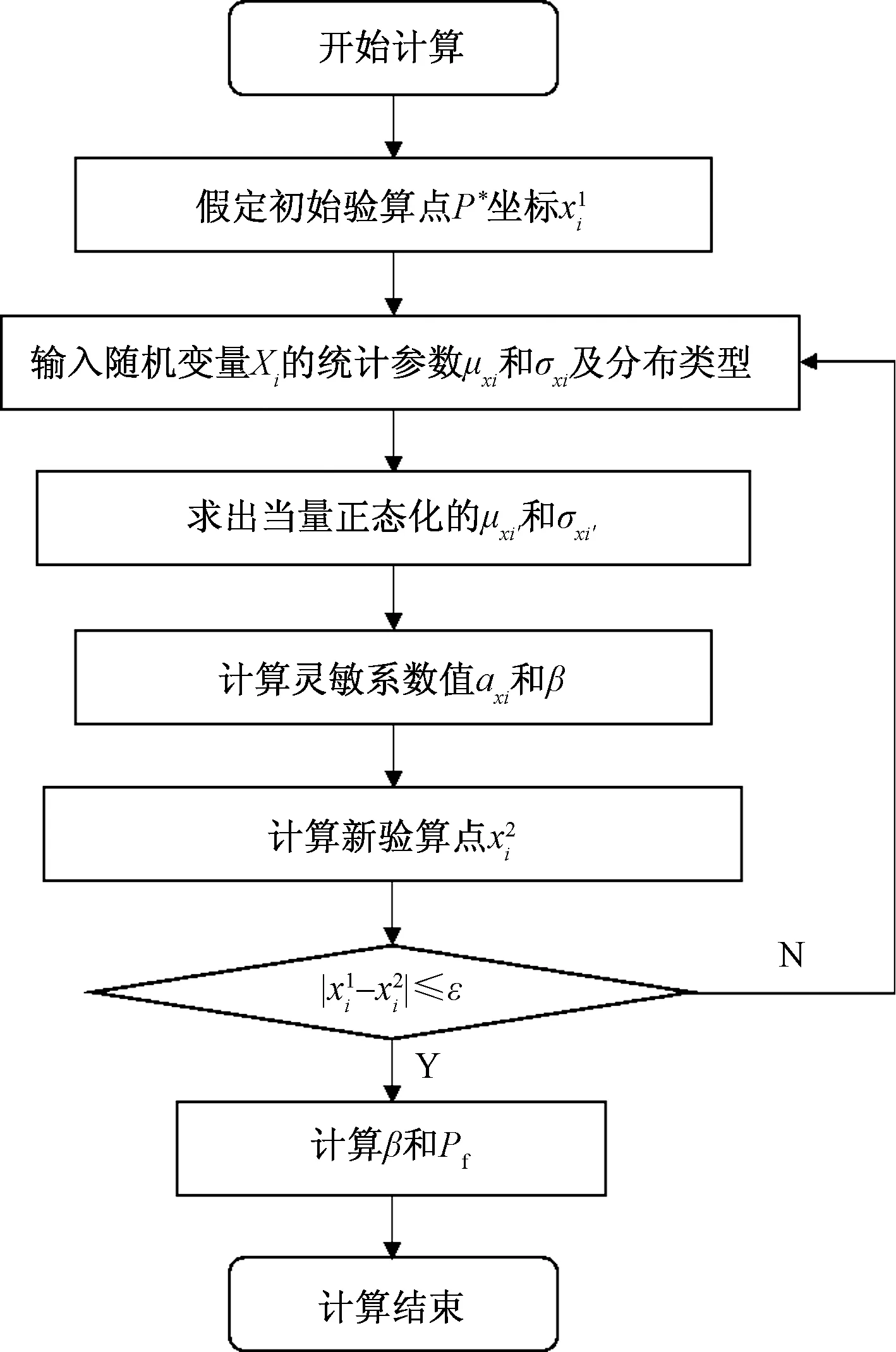
图6 JC法计算流程图Fig.6 JC method flow chart
2.2 堤防渗流破坏极限状态方程
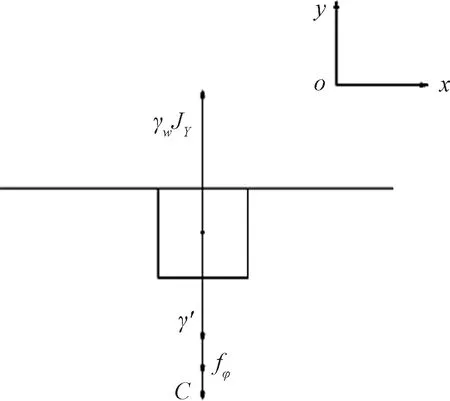
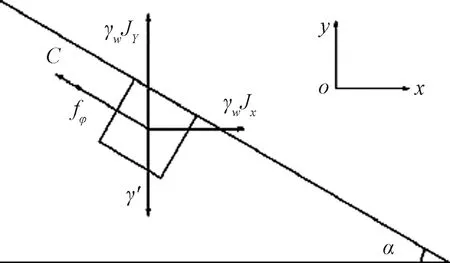
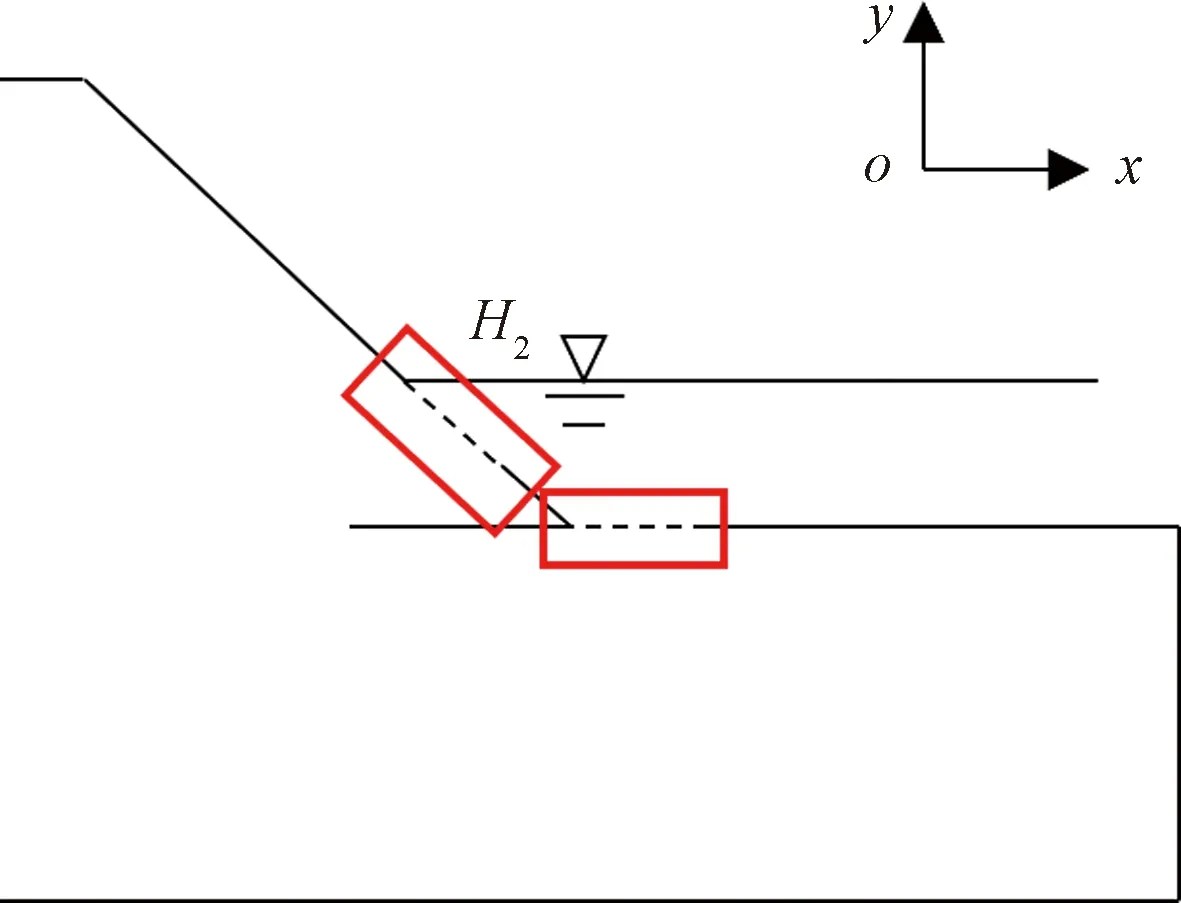
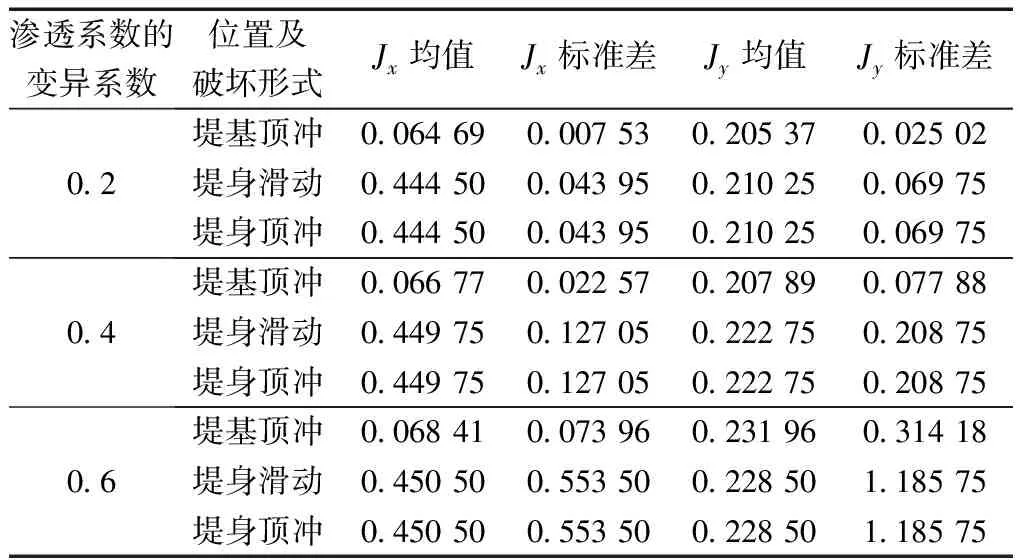
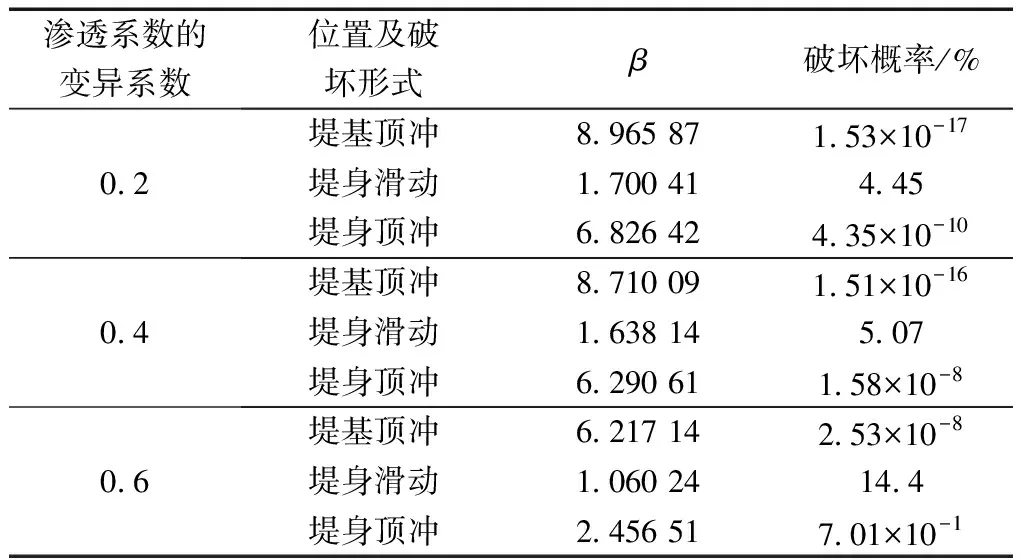
堤防的渗流破坏极限状态方程是用于判断堤防稳定与否的关键依据。工程中对渗透破坏稳定性的判别准则是将渗流场中的最大水力梯度值Jmax和土体的临界水力梯度Jc相比较,如果Jmax 图7 堤防典型断面横剖图Fig.7 Section plane of the levee 由于迎水坡水位较高,土体是受到水的压力作用的,不易发生破坏,所以渗流危险区域取堤基渗流出口区域①和背水坡堤身区域②。 2.2.1 堤基渗流出口区域 考虑此处土体在自下而上的渗流条件下发生顶冲破坏,单元土体的受力分析如图8所示,得到此处的极限状态方程为 g(x)=γ′+fφ+C-γωJY (10) 式(10)中:γ′ 为土体的浮容重;fφ为单元土体破坏面上所产生的摩擦力;C为单元土体破坏面上所产生的黏聚力;γω为水的容重;JY为竖直方向的水利梯度。考虑到土体在渗流作用下发生松动,土体的摩擦阻力就不存在了,所以安全起见可以忽略摩擦力的影响,则极限状态方程为 g(x)=γ′+C-γωJY (11) 图8 堤基单元土体受力分析图Fig.8 Force analysis diagram on dyke foundation unit 2.2.2 背水坡堤身区域 背水坡土体在渗流作用下需考虑两种破坏形式,一种是土体在渗透力作用下垂直于坡面的方向发生顶冲破坏,另一种是沿坡面方向发生下滑破坏。对于单元土体受渗流作用发生垂直于坡面方向的顶冲破坏时,其受力分析如图9所示,此时极限状态方程为 g(x)=γ′cosa+fφ+C-γωJYcosa-γωJxsina (12) 式(12)中:a为坡面与水平方向的夹角;Jx为水平方向的水力梯度。 fφ=(γ′sina+γωJxcosa-γωJYsina)tanφ (13) 式(13)中:φ为土体的内摩擦角。 图9 垂直坡面发生顶冲破坏受力分析图Fig.9 Force analysis diagram of failure vertical to slope surface 对于单元土体受渗流作用沿坡面发生滑动时,其受力分析如图10所示,此时极限状态方程为 g(x)=γωJYsina+fφ+C-γωJxcosa-γ′sina (14) fφ=(γ′cosa-γωJYcosa-γωJxsina)tanφ (15) 图10 沿坡面发生滑动破坏受力分析图Fig.10 Force analysis diagram of failure along the slope 以上为堤防在渗流作用下不同破坏形式的极限状态方程,极限状态方程中Jx、JY、C、φ为随机变量,因此需要知道各随机变量均值及标准差,结合JC法便可以求得堤防渗流破坏的可靠度。 结合上述堤防模型及极限状态方程,分析不同渗透系数变异性下的堤防渗流破坏概率。由于土体渗透系数的不确定性,水力梯度较大值不会只出现在一个位置,所以应对危险区域内的不同位置进行水力梯度统计。通过以上水力梯度云图可以发现堤脚附近水力梯度较大,将该区域作为堤防渗流破坏的危险区域,具体位置如图11虚线处所示。堤防土体参数设置服从正态分布,具体如表1所示。 表1 土体材料参数Table 1 Soil materials parameters 图11 水力梯度统计区域示意图Fig.11 Statistical region sketch of hydraulic gradient 将1 000次随机渗流分析的结果进行统计分析,将计算得到的数据采用SPSS软件作统计分析,经拟合、K-S检验后得到水力梯度服从正态分布。对区域处所有节点进行遍历计算,求得边界各节点处的破坏概率,在堤基及堤身不同的破坏形式分别各取破坏概率最大的位置点进行分析,结果如表2所示。 表2 不同破坏形式下破坏概率最大区域水力梯度统计结果Table 2 Statistical results of hydraulic gradient in regions with highest failure probability under different failure modes 堤基处破坏形式往往是垂直于堤基的顶冲破坏,从表2数据可看出,堤基处x方向的水力梯度均值及标准差相较y方向小很多,堤身处x向和y向的水力梯度差异则相对较小。变异系数较小时对堤防各方向水力梯度均值的影响较小,对标准差存在较大影响。不同变异条件下,堤身发生滑动破坏与发生顶冲破坏概率最大的位置为同一点。 表3 堤防渗流破坏计算结果Table 3 Calculated results of seepage failure of levee 表3为堤防渗流破坏计算结果,可以看出,在以上变异性条件下,堤防的堤基处发生渗流破坏的概率较小,几乎不会发生破坏。堤身处发生顶冲破坏的概率同样较小,相比之下在渗流作用下,渗透系数变异性增大,堤身发生滑动破坏的概率也会随之增大,变异系数0.6时,堤身发生局部滑动破坏的概率接近14%,该概率下的堤防存在发生破坏的可能。 以一典型堤防断面为例,构建了堤防渗流随机有限元计算模型,分析比较了渗透系数随机条件下水头和水力梯度的均值和标准差情况,根据分析结果选取堤防渗流不同破坏区域单元土体进行受力分析并构造了堤防渗流破坏的极限状态方程,最后结合JC法对堤防的渗流破坏进行可靠度分析和破坏概率计算,得到了以下结论。 (1)稳定随机渗流条件下,渗透系数变异性的变化对渗流场水头和水力梯度的标准差存在一定影响,变异系数变大标准差随之增大,变异系数增大,堤防发生局部渗流破坏的概率增大。 (2)通过不同区域的受力分析可构建相应的堤防渗流极限状态方程,从而可以综合考虑堤身与堤基区域可能发生的破坏。 (3)通过JC法理论和渗流随机有限元方法进行堤防渗流的可靠度分析,可得到堤防不同位置发生破坏的概率,为实际工程的稳定分析提供可靠的依据,具有一定的应用价值。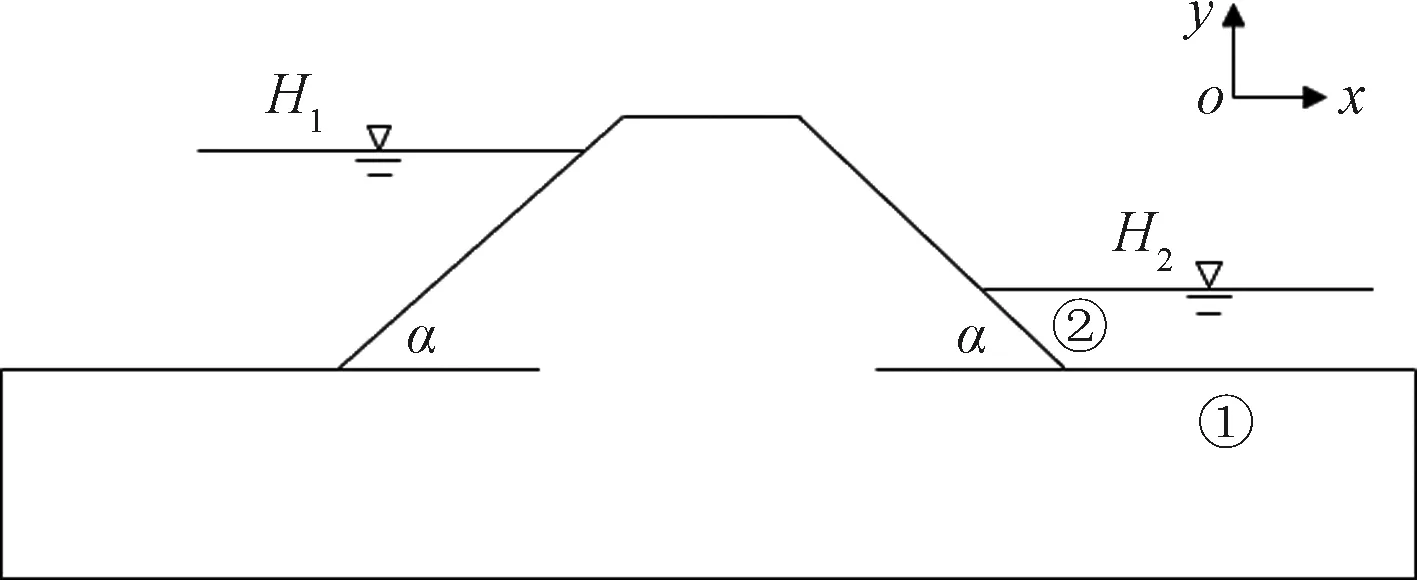

2.3 堤防渗流稳定可靠性分析

3 结论
