离子型金属聚合物复合材料的分数阶建模及二阶滑模控制

陈靖威, 黄梁松, 李甜甜, 李连鹏, 李玉霞

(山东科技大学山东省机器人与智能技术重点实验室，青岛266590)

离子型金属聚合物复合材料 (IPMC)[1]是一种电驱动智能复合材料，能够在外加电场的驱动下实现大幅度的弯曲形变，撤去电场后又能快速恢复至初始状态。近年来，由于其作为致动器具有致动电压低(1～5 V)，响应速度快，摆动位移大，可根据需要裁剪成任意形状且柔韧性好等特点，引起大量国内外学者进行了深入的研究与探索。美国NASA(National Aeronautics and Space Administration) 的 JPL(Jet Propulsion Laboratory)实验室用 IPMC 驱动器制造了与自动刮雨器相类似的除尘刷，用于太空仪器表面的除尘[2]；美国密歇根州立大学的Tant等设计了一种用 IPMC 驱动的机器鱼[3]；日本Eamex公司开发了以 IPMC 作为驱动材料的商业化产品人工鱼[4]；日本的名古屋大学研制了基于 IPMC 材料的泳动机器人[5]。因此，IPMC在仿生学、生物医学和微机电等领域的应用前景十分广阔。

分数阶系统，即是用分数阶概念里的导数和积分算子来代替传统整数阶动力系统当中的导数和积分，近年来受到了越来越多的关注。国外学者Sabatier指出采用分数阶模型可以有效地模拟大量的物理现象[6]。针对IPMC模型，Bao等证明了IPMC具有分形电极结构[7]。并由Caponetto在2008年确定了能够在较大的频率范围内描述IPMC执行器动态特性的分数阶传递函数[8]。证明了IPMC可以用具有长期时间或空间依赖现象特性的分数阶系统来表示，即建立一个分数阶IPMC模型能更好地描述它的运动特性。

在大多数情况下，滑模是通过向控制或观测系统中注入一个非线性不连续项来获得的，该项取决于输出误差。在设计不连续注入时，系统的运动轨迹必须保持在误差空间的某个滑动面上，产生的运动称为滑模[9]。滑模控制方法由于其具有有限时间的收敛性和对不确定情况的强鲁棒性等优点，得到了广泛的应用。本文根据Davila在2005年提出的二阶滑模控制观测器[10]，设计了一个基于分数阶的二阶滑模控制器，从理论方面论证了其可行性，并在仿真与实验两个方面分别与分数阶PIλDμ控制方法作对比，证明所提出的控制器具有更好的控制精度。

1 实验平台的搭建

离子聚合物是IPMC的重要组成部分，也是用来区分膜体种类的重要依据，主要分为全氟磺酸离子聚合物(Nafion)和全氟碳酸离子聚合物(Flemion)两种，通常选用美国杜邦公司生产的Nafion膜作为IPMC的基底膜。除了基膜外，还有上下表面的电极，通常为各种贵金属材料，如铂、钯、金和银等。值得注意的是，电极和基膜的界面特性对IPMC致动器的变形特性十分重要，通常可以对离子交换膜进行打磨处理，然后对糙化后的基膜采用浸泡还原的方法沉积电极层，所获得的电极与基膜相互渗透，可以极大提高电极与基膜的接触面积。图1为IPMC致动器结构图。

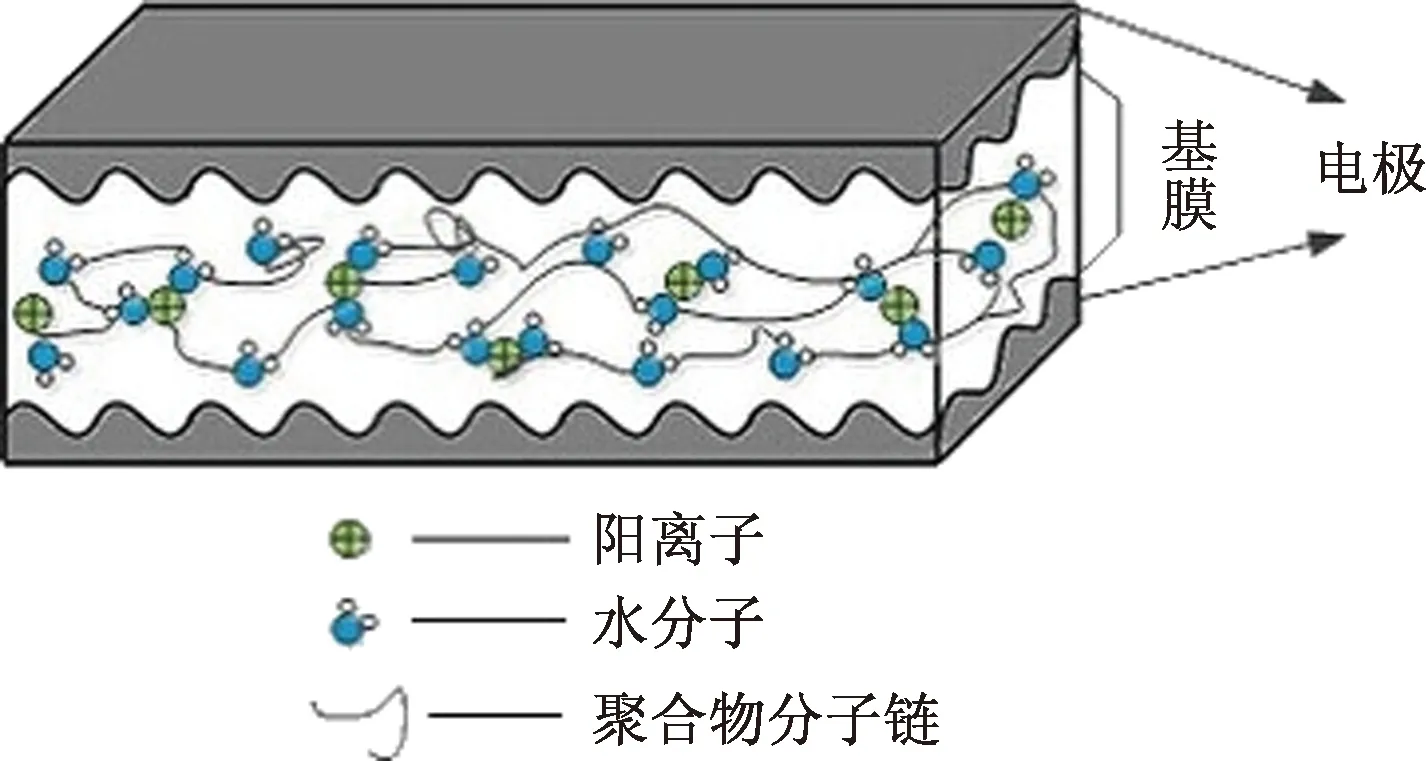
图1 IPMC致动器结构图Fig.1 IPMC actuator structure diagram

实验平台如图2所示，使用LABVIEW搭建了上位机部分并通过RS485与控制器进行串口通信，可以实现IPMC性能测试和输出位移控制两种功能。

图2 IPMC致动器实验平台Fig.2 IPMC actuator experimental platform

本实验平台的硬件主要包括控制器芯片、电源模块、可调电压输出模块、数据转换传输模块、激光位移传感器等。

(1)控制器芯片选用TI公司的TMS320C28335浮点DSP(digital signal processing)，该控制器相比于以往的DSP，多了一个MAC单元，具有运算速度快、数据及程序存储量大等优势，可满足实验平台功能需要。

(2)电源模块主要为开关电源直接供电220 V转24 V，为激光位移传感器供电24 V，为控制器芯片供电+3.3 V和+1.9 V，为IPMC致动器提供可调的输入电压。

(3)可调电压输出模块是为了满足实验中IPMC致动器两极的电压不仅要有直流电压，还要有正弦电压。所以为了满足需要，该部分采用了正弦波脉宽调制法(SPWM)，该方法中使用的驱动电路是全桥驱动芯片HIP4082IB，直流可调降压电源为LM2596S。

(4)数据转换传输模块中，使用的模数转换芯片为ADS8688，吞吐量可达500 kSPS；数字隔离器为ISO7241M，它具有四通道配置和输出使能功能，传输速度最高可达150 Mbit/s。

(5)为了实现IPMC致动器尖端位移的检测，本实验平台选用美国邦纳公司生产的L-GAGE LE250激光位移传感器作为检测设备。它带有显示屏，在量程范围(位移100～400 mm，电流0～10 V)内可以实时显示当前的测量位移和输出电流。

使用该实验平台，对IPMC薄膜施加一个电压为2 V，频率为10/2π Hz的正弦电压，可得其尖端位移的曲线如图3所示。

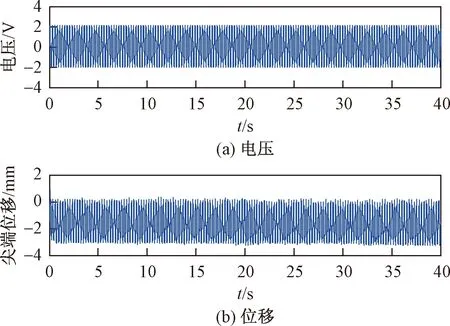
图3 驱动电压2 V、10/2π Hz时的尖端位移曲线Fig.3 Tip displacement curve when driving voltage is 2 V and 10/2π Hz

并且可以得到在该正弦电压下的输入输出关系图如图4所示，可以清楚地看出IPMC具有的磁滞特性。

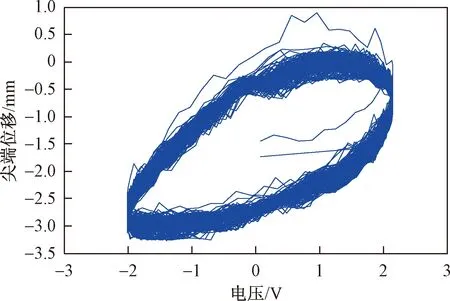
图4 IPMC的输入输出关系Fig.4 The input/output relationship of IPMC

2 IPMC致动模型的建立

2.1 分数阶微积分

早在300多年前，随着古典微积分概念的提出，数学家们就推导出了分数阶微积分，虽然仅仅是纯数学理论分析和推导，但也受到了众多学者的青睐。直到19世纪后期，分数阶微积分理论才开始逐渐在实际工程领域中得到初步的应用[11]。近年来，由于运用传统控制理论和方法无法达到期望指标，更无法满足人们对控制精度日益提高的要求，激发了学者们将分数阶微积分理论应用在实际工程的研究热情以及对分数阶领域进行更加深入的探索。

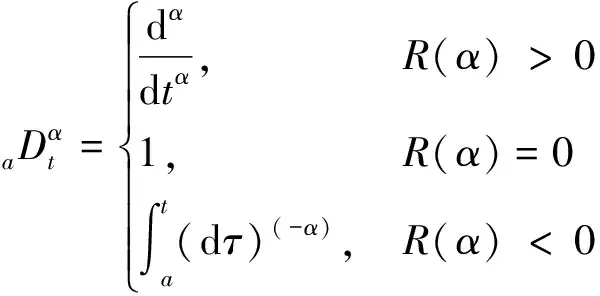
(1)

分数阶微积分普遍定义如下。

Riemann-Liouville 分数阶积分定义：存在α>0,t≥0时，f(t)被定义为

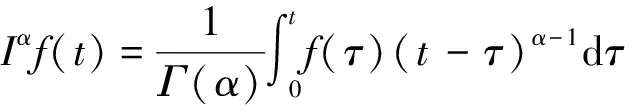
(2)

式(2)中：Γ表示欧拉伽马函数：

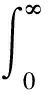
(3)

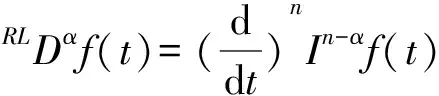
(4)

Caputo 分数阶微分定义：存在α>0,t≥0时，f(t)被定义为

(5)

当α∈(0,1)时，Riemann-Liouville与Caputo分数阶微分之间的联系为

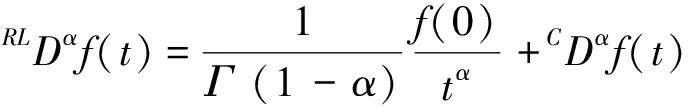
(6)

2.2 IPMC分数阶建模

Sun在2014年的时候提出了一个基于IPMC的传递函数模型，分别采用了线性不可逆电动力学模型和动力学模型对离子聚合物-金属复合材料的性能进行了分析[12]。其中第一个模型根据Onsager方程准确地预测了其静态特性，而第二个模型能够揭示其磁滞特性。通过这两个模型推导出的IPMC动力学传递函数模型将能较好地拟合出IPMC的实际运动效果。

该传递函数模型如下：

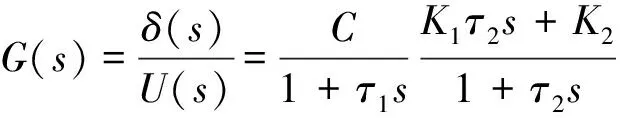
(7)

式(7)中：C、τ1、τ2、K1、K2为需要辨识的参数。

通过上述的实验平台，对IPMC采用驱动电压为2 V，频率为10/2π Hz的正弦信号，得到所需的输入输出数据，随后结合人工蜂群算法来对上述传递函数中的5个未知参数进行辨识。人工蜂群算法是由土耳其学者提出的一种基于蜜蜂群体觅食行为的智能优化算法[13]。该算法相比粒子群算法、蚁群算法等其他智能优化算法，具有参数少、易于实现、鲁棒性较好等优点，而且全局搜索和局部搜索在每次迭代过程中都会进行，这一点不仅增加了找到最优解的概率，还相对减小了陷入局部最优的可能性。整个优化步骤如下。

(1)初始化ABC(artificial bee colony)算法中的各种参数、食物源的数量SN、食物源的最大循环次数和终止循环次数。

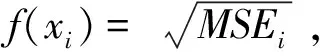
本次人工蜂群优化算法中，设蜜源数N=100，参数limit为100，最大迭代次数为500，程序运行次数为100。最终得到5个待辨识的参数分别为：τ1=0.145 2，τ2=12.722 4，C=1，K1=1.275，K2=-22.246 8。即传递函数模型为

(8)

得到了IPMC整数阶的传递函数，此时再根据上述的输入输出数据，采用结合了泰勒计数法和梯度法的Marquardt算法将其转化成分数阶模型[14]。该算法实际上是使模型满足：

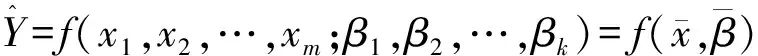
(9)

(10)

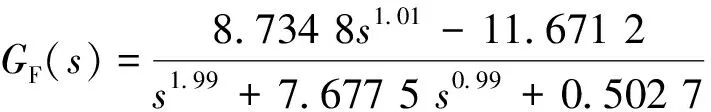
(11)

根据图5可以看出分数阶模型与实验数据的拟合度更高，即分数阶模型能够描述出IPMC所具有的非整数阶特性。

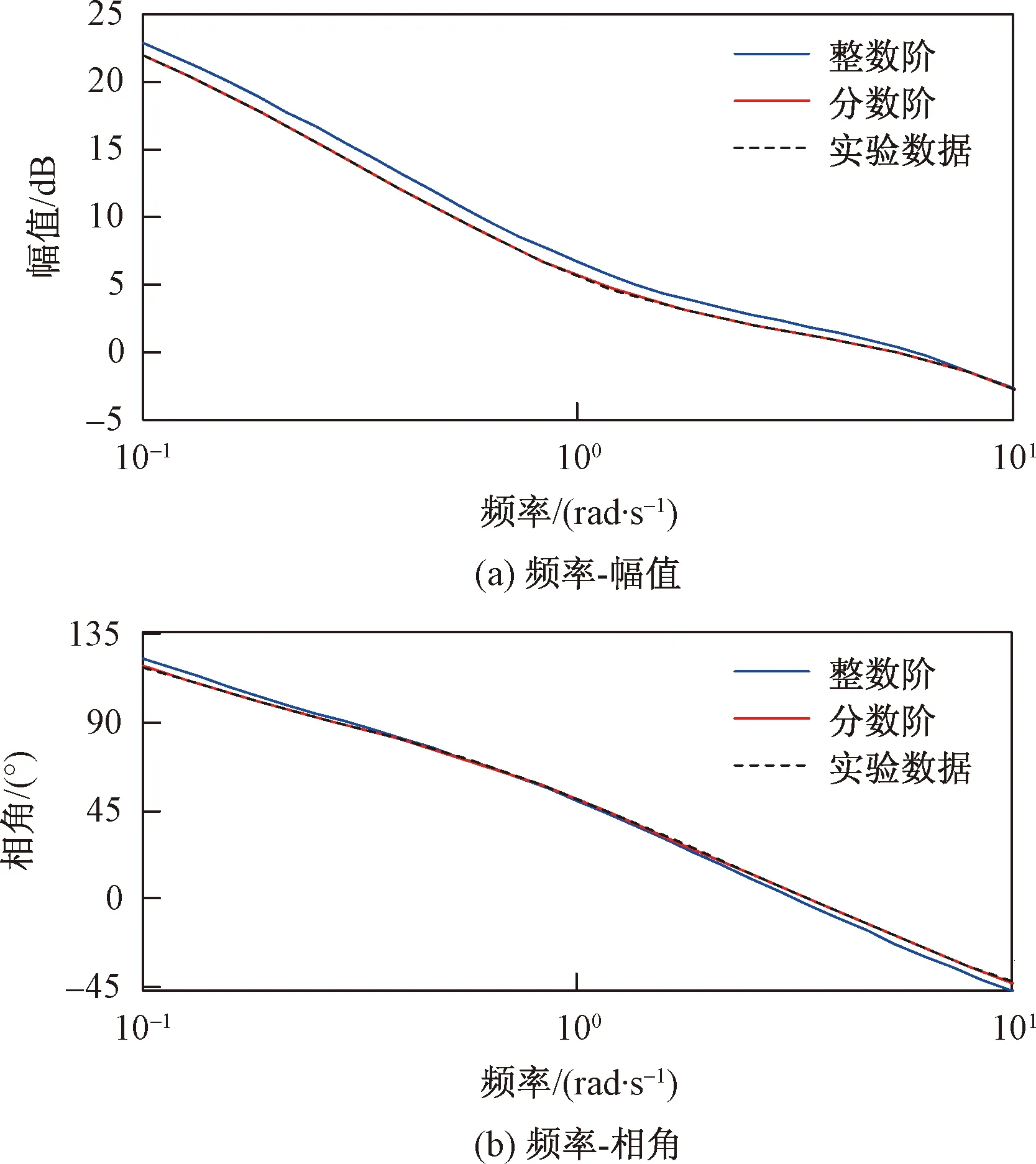
图5 分数阶模型、整数阶模型和实验输出结果比较Fig.5 Comparison of fractional order model, integer order model and experimental output results

3 基于分数阶的二阶滑模控制器设计

考虑到一个受动态模型控制的带扰动的一阶分数阶系统：

CDαx(t)=ax(t)+bu(t)+φ(t)

(12)

式(12)中：α∈(0，1)是已知的非整数阶微分；x(t)∈R是测量出的输出变量；u(t)∈R是一个可调输入；a∈R是一个不确定的参数；b是一个已知的正常量；φ(t)是一个不确定的干扰。

基于上述分数阶系统，设计了一个基于分数阶的二阶滑模控制器为

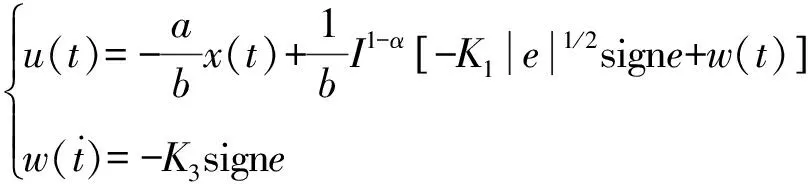
(13)

设xr(t)为一个足够光滑的参考面，此时，需要证明该控制器能够保证跟踪误差能在有限时间归零。误差e可以表示为

e(t)=x(t)-xr(t)

(14)

考虑跟踪误差变量的动态特性：

CDαe(t)=ax(t)+bu(t)+φ(t)-CDαxr(t)

(15)

此时把除了可调输入的其余三项合并为

Δ (x,xr,t)=ax(t)+φ(t)-CDαxr(t)

(16)

很容易可以证得闭环跟踪误差动力学满足这种形式：

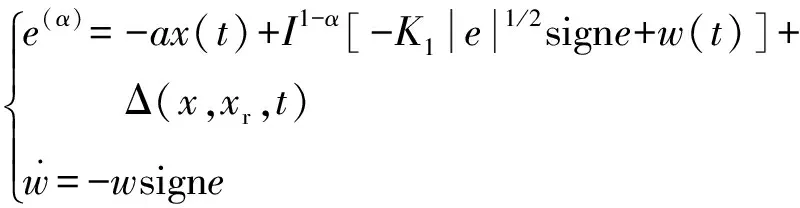
(17)

定义：

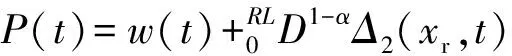
(18)

此时：

Δ2(xr,t)=φ(t)-CDαxr(t)

(19)

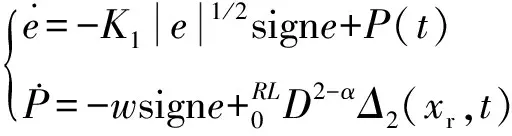
(20)

根据式(19)可得：

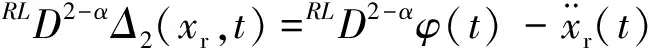
(21)

此时，根据式(12)，假设受控输出x(t)的时间演化足够光滑，即系统输出x(t)由一个已知的常量xd和有限时间td组成，即：

|RLD2-αx(t)|≤xd,t≥td

(22)

在该假设的基础上，扰动φt，参考面xr(t)以及不确定的常量a有以下关系：

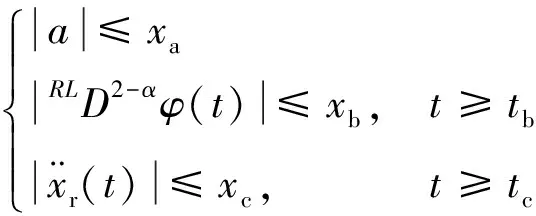
(23)

式(23)中：xa、xb、xc为已知的常量；tb、tc为有限时间。

根据式(22)～式(23)，推得：

RLD2-αΔ2(xr,t)≤xb+xc

(24)

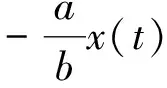
针对所提出的控制器，其整数阶模型和分数阶模型在有限时间归零条件下是等价的，所以通过形式更加简单的整数阶模型进行李雅普诺夫定理的证明，简化后的整数阶模型为

(25)

转换Lyapunov函数为

(26)

式(26)在任何地方都连续，但是在x1=0处不可微。

因为由式(25)得到的微分子集的状态轨迹φ(t,x0)是绝对连续函数，因此V[φ(t,x0)]是一个连续时间的函数，但于V(x)缺少Lipschitz性质，所以无法保证V[φ(t,x0)]的绝对连续性和它的可微性是无处不在的。然而V(x)是除了在S={(x1,x2)∈R2|x1=0}处是连续可微的。很容易看出系统(13)的轨迹只是穿过曲面S，不能停留在上面，除非达到原点x=0。这意味着V[φ(t,x0)]几乎在每一个t都是可微的，并且这些点导数都可以用链式法则这种普通的计算方法得到。这表明，在运用Lyapunov定理时，可以只考虑V(x)可微的点。

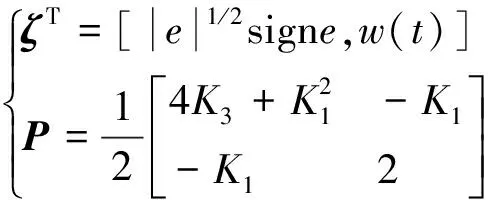
(27)

注意V(x)在x=0处是连续不可微的。当K3>0时为正定无界，即：

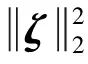
(28)

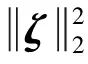
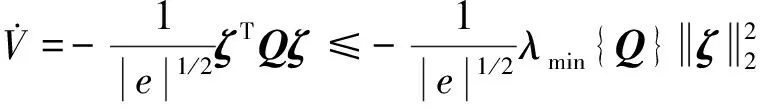
(29)

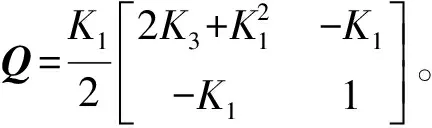
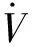
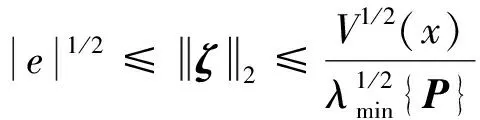
(30)

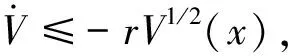
(31)

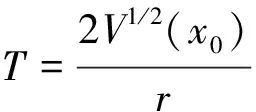
4 仿真和实验研究

4.1 仿真研究

选取了目前在分数阶控制系统中较为常用的分数阶PIλDμ控制算法与所提出的基于分数阶的二阶滑模控制算法作对比。分数阶PIλDμ控制算法是分数阶微积分理论与传统PID控制算法的融合，在传统PID控制的三个参数KP、KI、KD的基础上，又多了两个可调的参数λ和μ，所以控制器参数的正定范围变大，能够更加灵活地对受控对象进行控制，得到更好的控制效果[15]。设计PIλDμ控制器如下：

GFOPID(s)=0.95+2.5s0.98+0.04s-1.9

(32)

图7所示即为上述仿真系统中的单位负反馈阶跃响应。其中FOSM表示基于分数阶的二阶滑模控制，FOPID表示分数阶PIλDμ控制。

由图7、表1可见，在上升时间、超调量、调节时间三个方面，基于分数阶的二阶滑模控制都要小于分数阶PIλDμ控制。即从仿真结果来说，基于分数阶的二阶滑模控制器的控制效果要优于分数阶PIλDμ控制器。

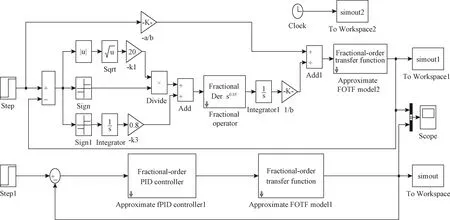
图6 分数阶PIλDμ与基于分数阶的二阶滑模控制框图Fig.6 The control block diagrams of fractional PIλDμ and second order sliding model based on fractional order

图7 FOSM与FOPID的比较Fig.7 Comparison of FOSM and FOPID

表1 两种控制器的数据对比

4.2 实验研究

已经通过第一章介绍的实验平台对IPMC致动器进行了性能测试，得到了实验数据，下面则运用该实验平台对IPMC尖端位移进行控制。通过上位机发送出期望位移，RS485接收到该位移并进行相应的控制器的计算，然后将计算得到电压附加到IPMC致动器上，以实现对IPMC致动器的控制。软件流程图如图8所示。

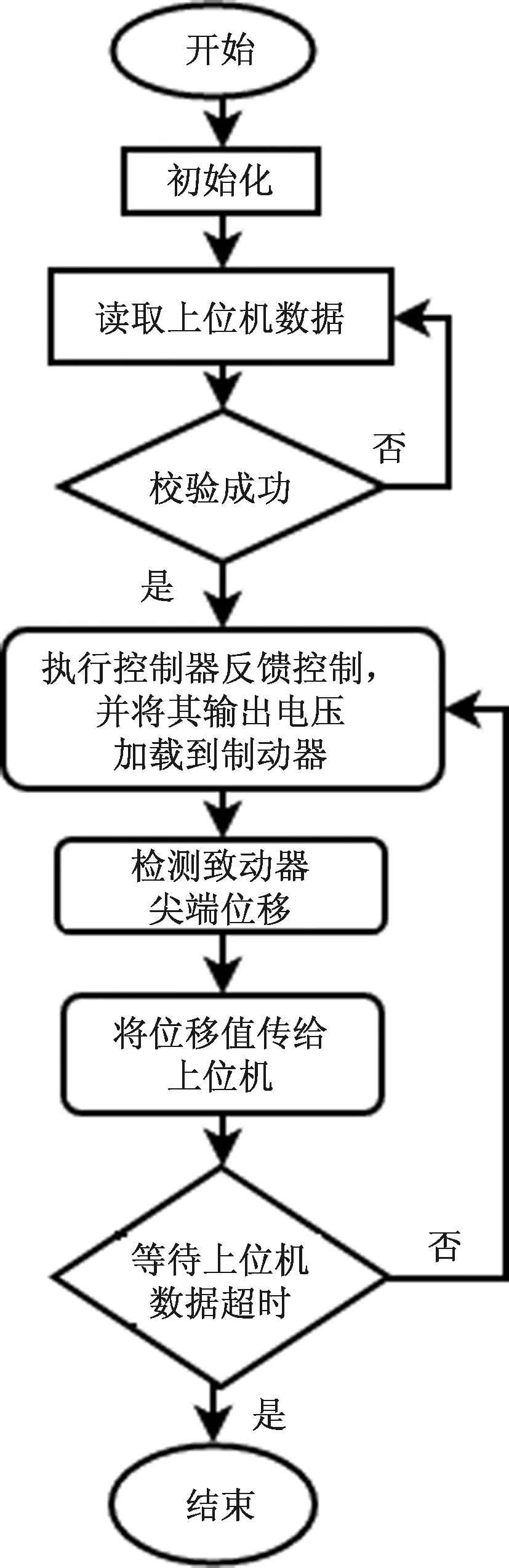
图8 控制模式软件流程图Fig.8 Software flow chart of control mode

由文献[14]可知，分数阶PIλDμ控制算法中的微分项对IPMC控制的影响很小，所以在本实验中忽略其参数KD和μ。可以通过上位机随时更改分数阶PIλ控制算法中的KP、KI、λ三个参数以及基于分数阶的二阶滑模控制算法中的α、K1、K3三个参数。通过对参数不断调节，以期望达到每种算法的最优跟踪效果。设定期望位移为幅值为3 mm，频率为1/2π Hz的正弦曲线。两种算法的最优跟踪曲线及误差分别如图9～图12所示。

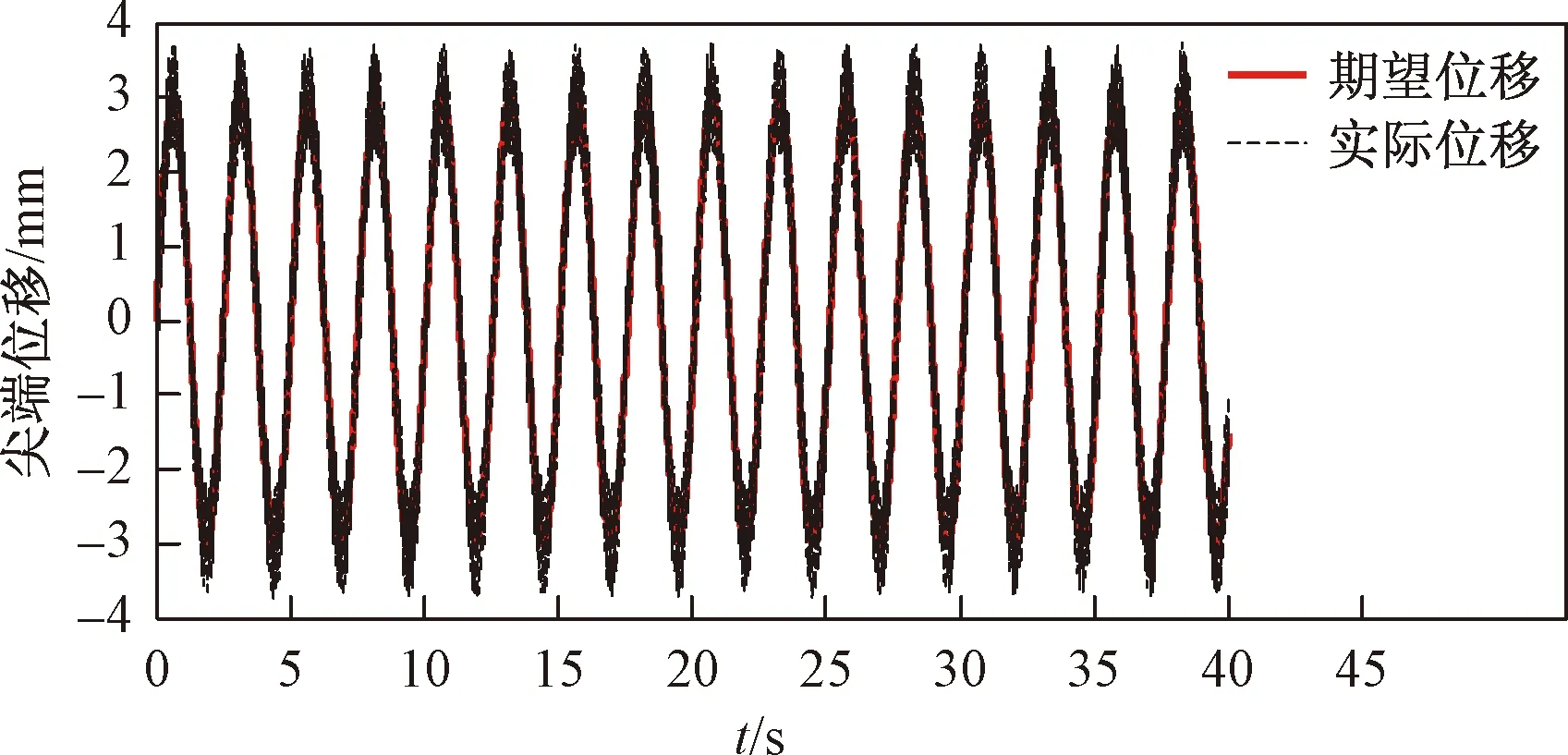
图9 分数阶PIλ控制时的输出曲线Fig.9 The output curve under fractional PIλcontrol

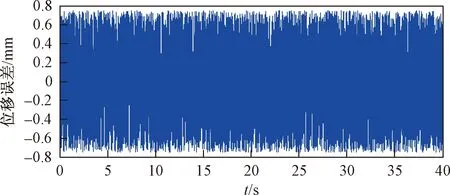
图10 分数阶PIλ控制器的控制误差Fig.10 The control error of fractional PIλcontroller

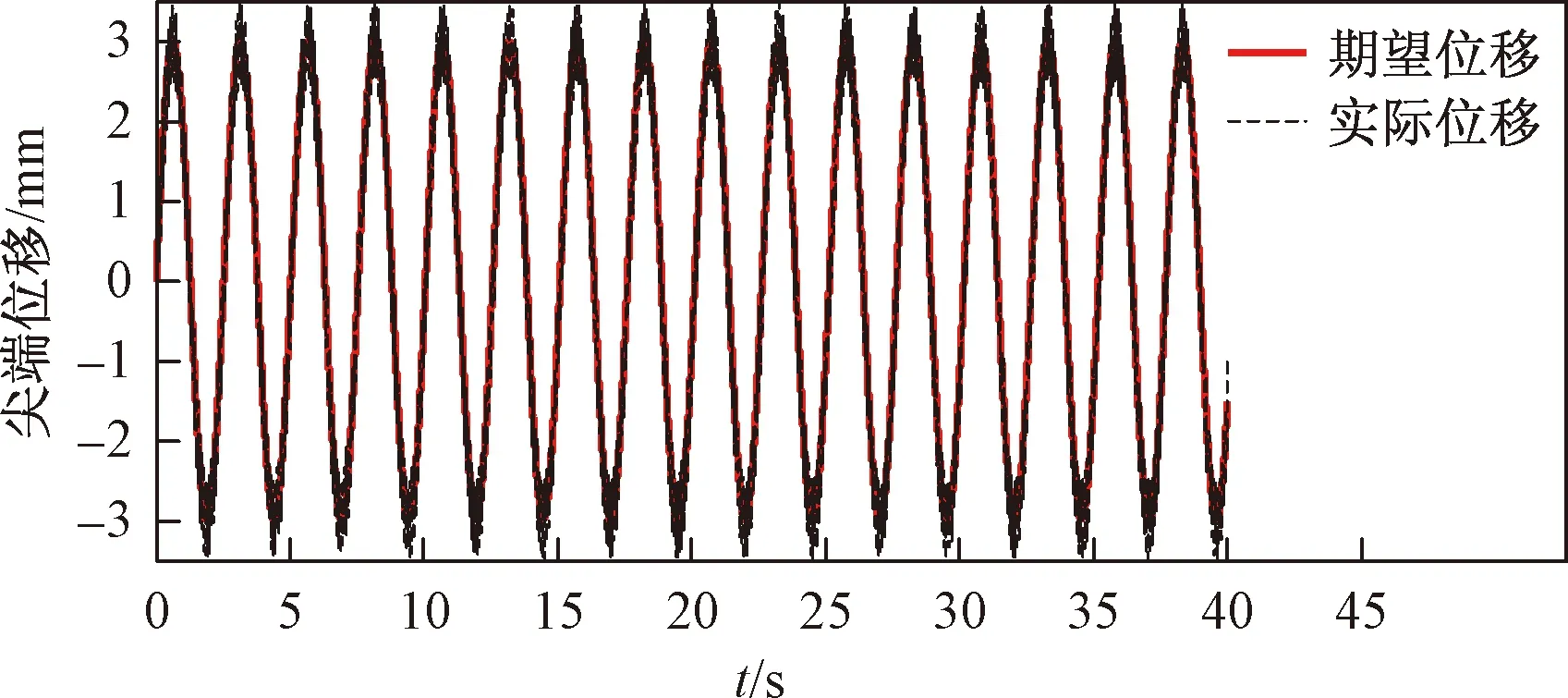
图11 基于分数阶的二阶滑模控制器的输出曲线Fig.11 The output curve under second order sliding mode controller based on fractional order

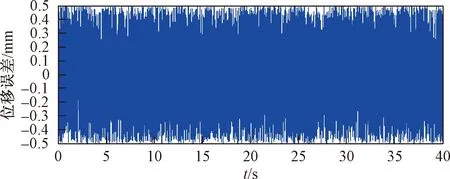
图12 基于分数阶的二阶滑模控制器的控制误差Fig.12 The control error of second order sliding mode controller based on fractional order

由图9～图12可以看出，基于分数阶的二阶滑模制器的跟踪效果要好于分数阶PIλDμ控制器，且位移误差更小。通过计算均方根误差可得，基于分数阶的二阶滑模制控制器的均方根误差为RMSE=0.289 5,分数阶PIλDμ控制器的均方根误差为RMSE=0.431 9。因此可以得出，所提出的控制器在针对IPMC实际的控制效果上要优于传统的分数阶PIλDμ控制器，且拥有较好的控制效果。

5 结论

根据IPMC特性，搭建了实验平台，并为IPMC薄膜施加了驱动电压为2 V，频率为10/2π Hz的正弦电压，得到了实验数据。随后，选用人工蜂群算法对参考模型中的未知参数进行寻优，得到了整数阶模型；再使用Marquardt算法辨识出了分数阶模型。通过两种模型与实验数据的比较可以得出，分数阶模型与实验数据拟合度更高，能更精确地反映出IPMC的非整数阶特性。

然后针对该IPMC的分数阶模型，设计了一个基于分数阶的二阶滑模控制算法，并从理论方面证明了其合理性。后将其与常用于分数阶系统控制的分数阶PIλDμ算法进行对比，并分别采用仿真与实验两个方面进行。无论是仿真结果还是实验结果，所提出的控制算法均优于分数阶PIλDμ算法。即证明了所提方法是可行的，可以更加精确地控制IPMC致动器。

通过实验过程可知，控制器参数不仅关系着控制器本身，而且对于分数阶系统的影响也很大。所以，下一步应该针对所提出控制器的参数进行深入的研究，提供一种有效的参数选取方法，以便在任何控制情况下都能高效地设计出所需的控制器。