基于地磁传感器解算旋转体姿态的方法

邵伟平，孙 林，张嘉易，郝永平，杨 超

(沈阳理工大学 机械工程学院，沈阳 110159)

随着磁场测量技术的发展，利用地磁场对运动载体进行测姿的精确度不断提高，同时各个国家也非常重视对地磁导航测姿技术的研究。美国首先提出了基于地磁异常场等值匹配的MAGCOM系统，在2006年F.Goldenberg针对飞机的地磁导航系统研究出了基于地磁场图的测速定位方法。近些年国内对地磁导航测姿技术的研究同样发展迅速，例如：运用平均绝对差法对地面测量的地磁强度数据进行了匹配运算，分辨率达到50 m；采用捷联式地磁-太阳方位传感器解算弹体滚转角；将地磁感应圈传感器应用于火炮弹药上，测量转速并控制炸点等。

目前，对于智能弹药射击精度不断提高的要求，迫切需要能够精确测量旋转弹体的滚转姿态位置信息的方法来提高弹体弹道修正精度，进而提高弹体打击精度。

本文将地磁传感器角度解算方法应用到旋转弹体上，通过测量弹体在地磁场中的特性参数从而解算出弹体的滚转姿态信息，该方法原理简单，成本低，精度高，同时解算具有实时性，能够为弹体精确制导提供准确有效的数据信息。

1 原理分析

利用地磁传感器可以测量旋转体对地的滚转姿态，结合光电传感器可以测量相对旋转体的滚转姿态，其实验装置如图1，两侧利用电机提供反向动力使前后旋转体相对转动，将地磁传感器和光电传感器放置在同一水平面的后部旋转体上，同时将发光器件安装在光电传感器正上方的前部旋转体上，当发光器件与光电传感器相遇时便会产生感应信号，此时后部旋转体的当前角度值就是前部旋转体的当前角度值。

图1 实验装置示意图

2 地磁传感器角度测量方法

2.1 基于单轴地磁解算方法

2.1.1判断地磁信号有效值

将地磁传感器调节成单轴输出，通过DSP28335处理器对磁传感器信号进行实时处理，由于磁力计测试原理，当旋转体旋转一周时，地磁信号呈周期性近似正弦波形式输出电压值，即地磁每个输出值都唯一对应一个地磁的位置，可表示为f(t)=Asin(t)+g(t)，其中A为地磁电压幅值，t为采样时间，g(t)为干扰信号。当无干扰信号时，g(t)=0，此时f(t)=Asin(t)，当f(t)=Asin(t)=0，可求得t=kπ时相邻采样点间电压最大差值ΔVmax，离散型数字信号有：

ΔVmax=Asin(kπ+Δt)-sinkπ=AsinΔt

根据实验台试验采样特性可以得知，当最高转速为20 000 r/min时，采样数m大于400。已知地磁信号电压幅值为3.3 V，即A=3.3。由此可以得到：

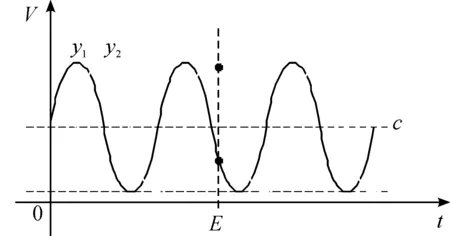
ΔVmax=AsinΔt

本文采用均值滤波算法对地磁信号电压幅值进行滤波，设每10个采样点为一组。

S=∑X1[i]，其中1≤i≤10

U=S/N，其中N=10

运算中每加一个点i=i+1，求相邻两点间的差值：

D1[i]=|X1[i]-X1[i-1]|

将开始连续的10个点中除去第一个点外，满足D1[i]>ΔVmax且D1[i-1]>ΔVmax的点X1[i-1]值作为临近点后计算均值，令逐点推进计算。逐点滤波有效区域值确定为

ΔV=6×ΔVmax=0.035

判断地磁信号是否为有效信号，当地磁信号值|X1[i]-U|≤ΔV为有效信号，当地磁信号值|X1[i]-U|>ΔV为无效信号。

2.1.2转体滚转角度及转速的计算

假设图2为采样的地磁信号电压幅值，横坐标为电压采样点数量，纵坐标为电压值，采样周期为T，通过对零点C的标定以及采样周期点数对转体的转速和滚转角进行结算。当转体旋转一周的时候，地磁信号电压幅值为一个周期，转体滚转角为360°，此时这个周期的地磁信号电压采样点都唯一对应着转体滚转角的度数。因此通过周期采样点数就能求得转体的滚转角。

图2 地磁信号电压幅值

首先是在线调节，算法的所有数据都基于在线采集数据。在嵌入式算法程序中，使用定时器定时采集地磁信号，设采集地磁电压速率为V1，采集地磁电压点数为P1，采样时间为t1，则有关系式：P1=V1×t1。通过在实验台上对转体不同转速下采集地磁信号电压采样周期的调节，使得转体转速在1 000～15 000 r/min时，地磁信号电压采样点数P1控制在400～1 500之间。

其次，针对地磁信号电压不断变化的幅值，需要预先采集初始的2 000个电压采样点，对其进行最高电压Va和最低电压Ve的挑选。在挑选过程中，如何判断此Va最高电压，Ve为最低电压？将采集电压值Va与Va前实时解算逐点累加的电压均值U进行比对，若Va-4、Va-3、Va-2、Va-1均大于U，Va+1、Va+2、Va+3、Va+4均小于U，则证明Va为最高电压值。相反，若Ve-4、Ve-3、Ve-2、Ve-1均小于U，Ve+1、Ve+2、Ve+3、Ve+4均大于U，则证明Ve为最低电压值。通过大量Va和Ve，可以求得均值电压线Vc=(Va+Ve)/2，最大幅值电压差A=Va-Ve。通过已知Vc后，可以求出上中边界电压线Vb与下中边界电压线Vd。因为采样周期不变，设k为满足Vb

设波谷后的均值电压线Vc的采样点横坐标为h1，波峰后的均值电压线Vc的采样点横坐标为h2，即可求出峰线位置采样点的横坐标h：

h=floor[(h1+h2)/2]

最后，在解算旋转体滚转角时，标定求出的地磁信号波峰最高点为对应旋转体滚转角的0°，即为零点(标定旋转体零度位置点)。两个波峰线之间的采样点横坐标之差就是地磁信号电压幅值一个周期的采样点数量t1(也就是旋转体每转的采样点数量)。因为采样周期不变，所以当旋转体在匀速旋转时，可以通过电压周期采样点数t1和波峰零点坐标实时解算旋转体的滚转角，得出当前地磁信号电压采样点k对应的角度α：

值得注意的是，此处采样点数量是不断更新的，更新周期为T，所以起到变幅值预测的作用，抵制外界干扰，通过单轴地磁信号解算角度值，避免了波形出现上下端截止时造成的误差干扰。

已知地磁信号电压采样周期T和解算出的周期采样点数t1，可以求得转体的转速n和角速度ω：

2.2 基于三轴地磁解算方法

2.2.1滚转角解算

三轴地磁传感器，相对于单轴地磁传感器多了两个两两相互垂直的地磁传感器，由于在实验中没有俯仰角度，所以利用DSP28335处理器对双轴地磁采集的信号进行处理，通过示波器测量出的波形如图3所示。X轴和Z轴的电压幅值为0～3.3 V，首先对采集的信号进行均值滤波处理，再利用转换公式解算这些电压幅值得出旋转体滚转角度。

图3 X轴和Z轴的电压幅值

解算的旋转体滚转角就是旋转体在沿地磁传感器Z轴旋转时的X轴和Z轴的角度，也即是在垂直于转轴的平面内转轴坐标系和旋转体坐标系的夹角，如图4所示。

图4 旋转体滚转角示意图

可以看出旋转体的滚转角γ：

2.2.2对于旋转体滚转角度及转速的解算

通过已知采样的双轴电压幅值如图5所示，设X轴曲线为y1=A1sin(ω1t+φ)，Y轴曲线为y2=A2cos(ω2t+φ)，作垂直辅助线相交x轴于点E，可得出E时刻角度值θ=atan2(y1,y2)，θ∈[-π,π]，θ即为当前E时刻时旋转体的滚转角。当θ<0时，需要将角度归一化，θ=θ+2π。

图5 地磁双轴电压幅值

基于双轴地磁解算旋转体滚转角的准确性，根据在一个周期内两个时刻之差Δt，旋转体旋转了Δα的角度值，可以得出此时的角速度为ω=Δα/Δt，旋转体的转速为v=ω/2π。

通过使用单轴地磁传感器和三轴地磁传感器进行角度测量实验后，对两种传感器的性能进行了比较，如表1所示。

从表1可以看出：单轴地磁传感器成本低，适应于高动态，运算量为6 μs，可以适应各种环境，但是精度一般且采样率要求较高；三轴地磁成本高，运算量为3～4 μs比单轴低，对环境要求较高，高低动态都适用，由于通过双轴解姿所以精度非常高，对于采样率要求相对低。因为三轴地磁传感器对于以后的俯仰姿态解算有着重要作用，本文采用三轴地磁传感器。

表1 单轴和三轴地磁传感器的比较

3 对于前部旋转体的姿态解算

已知实验装置结构特点，前后部旋转体相对旋转，通过地磁传感器测得后部旋转体的滚转角，不考虑初始对准时，假设地磁位置指向即为后部旋转体的角度数据，记为α；同理，将前部旋转体的指向位置与初始角度的差值设为前部旋转体的角度，记为β；当光电传感器与光源信号触发时，产生感应信号，此时后部旋转体的当前角度值就是前部旋转体当前的角度值，即α=β。另外，须知两者本质上都是对地的绝对转角，只不过需要初始对准，确定0角度位置。

已知后部旋转体转速n1=1/T，T为后部旋转体的周期，单位为r/s，所以1/T也是频率。假设前部旋转体转速为n2，前面已经提及的光电传感器本质上给出了前部与后部旋转体相遇点的标识，已知n1解算n2。可以将前部与后部旋转体比作甲乙两人在圆形操场上跑步，先设定两人反向跑步，则有公式n1Δt+n2Δt=1，即n1+n2=1/Δt(其中1表示单位圈，Δt表示两人两次相遇的时间间隔)，得出结论1/Δt为两人的相对转速，同理可得两人同向跑步的情形，n1Δt-n2Δt=1。

所以现在的解算方法，n2=1/Δt-n1，其中Δt为两次光电传感器触发的时间间隔，Δt=τ·Dtm(τ为时间常数，Dtm为两次光电传感器触发间隔内的地磁采集点数)，1/Δt即为前部与后部旋转体的相对转速(频率)。

4 前部旋转体位置标定实验

由于在对前部旋转体进行滚转角度测量时，当前部旋转体在某一角度停止时，并不知道此刻角度的具体数值是多少，因此需要对其进行位置标定实验，并制作适合前部旋转体标定角度的0～360°角度圆盘，用于以后判断停止时的角度位置。

首先将前部旋转体固定在转台上静止不动，取其中一个点做上标记作为标定角度指针，设置后部旋转体转速为3 000 r/min，测试1 min后提取数据。然后再将前部旋转体随机固定在另外3个位置上，每次固定时都需要在空白圆盘上做上标记，最后通过4组角度数据绘制一个刻度圆盘后，再将前部旋转体固定在刻度盘90°的位置上，提取数据并进行对比，判断舵机是否停止在90°位置上。表2为舵机随机4次固定位置时的角度数据。如表3为舵机固定在90°时测试的角度值。

表2 舵机固定滚转角度数据截取片段

表3 舵机滚转角度为90°截取片段

实验结果表明：通过对前部旋转体停在4个角度位置的测试数据可以得出，即使把前部旋转体固定不动时，也会存在转体稍微抖动，造成测得的数据存在微小误差。从表2可以看出极差在4°以内，正常误差在1°～2°之间，对其进行一维线性标定后均值误差分别为：1.700 7°、0.904 1°、1.051 5°、1.765 8°，可以看出4个角度的标定标准差维持在2°以内，稳定性较好。通过表3测得的数据与刻度盘标定的90°对比可以看出，测量位置角度虽然存在微小误差但是还是非常准确。

5 结论

利用地磁传感器与光电传感器组合的方法可以实现对相对旋转体姿态的实时解算。经过对旋转体滚转角度解算的实验数据分析，旋转体停止不动时的最大角度误差小于4°，在合理实验误差范围内。解算滚转角位置的准确度非常高，能够利用低成本地磁传感器高精度的实时解算旋转体的滚转姿态提供实际意义。