基于系统动力学的装备维修级别决策研究

2020-04-22魏圣军吴法文汪文峰

兵器装备工程学报 2020年3期

魏圣军，吴法文，张琳，汪文峰，张搏，牛童

(空军工程大学研究生院，西安 710051)

装备的维修保障是使装备改善、恢复、保持规定的技术战术状态而实施的一切活动[1]。本世纪初，美国陆军依据未来战争和装备发展对维修保障的需求，开始研究论证推行装备维修工作体系由原来的四级维修体系向两级维修体系转型[2]。准确识别当今和将来不断出现的新技术及其在军事方面的应用，对未来战争发挥着越来越重要的作用，从而对军事能力结构变革和作战力形成产生重大影响[3]。地空导弹武器系统信息化程度高，装备故障自检要求严，现行维修任务分工和作业体系维修已不适应维修保障要求。依据相关文件要求，将地空导弹装备维修作业体系由基层级、中继级、基地级三级维修调整为部队级、基地级二级维修。

通过对武器装备各项指标、数据的科学分析，联系部队实际情况，确定维修等级，选择最合理修理方案，科学制定最佳维修方式和维修周期，提高武器装备完好率和可靠性，极大的缩短装备修理时间，节约装备修理成本，延长武器装备使用周期[4]。就地空导弹雷达装备来说，单位基层级主要是对分机、插件和重要部(器)件的随机备份，采用换件维修方法，基层级把整机故障定位隔离到单个可更换单元，并以备件更换的形式来保障装备；故障的单个可更换单元部件由大修厂、生产厂等基地级进行修复，但到目前来说，对于二级维修体制的讨论还仅限于在原则和方式方法上，至于实施二级维修体制的条件、时机和方法还有待于仔细研究，本文仅从人力资源系统角度运用系统动力学模型从仿真假设、仿真分析、参数分析进行仿真比较得出科学结论，确定实施二级体制的时机及条件。

1 二级维修体制构想

二级维修保障体制主要内容：加大地空导弹基层级对主要部件、插件的随机备份，基层级采用换件维修方法，基层级把整个系统故障定位隔离到单个可更换单元，并以备件更换的形式来保障装备；故障的单个可更换单元元件由基地级进行修复；基地级采用修复性维修方式，由基地级修理厂的专业技术人员在修理厂利用配套维修设备队装备系统、分系统、部件、组合件进行全面的检测、调整和修复，全面恢复装备的性能，同时，对基层级送来的故障件进行检测和修复；二级维修保障体制维修技术人员的确定方法和三级体制下基本相似，两种体制下基层级维修技术人员的确定方法是一样的；而二级体制下，基地级的大修系统和备件修理系统的维修技术人员确定方法和三级体制下也是一样，只是基地级事后维修系统的维修技术人员的确定思路采取三级体制下中继级事后维修技术人员的确定思路。在这种二级维修保障体制中，地空导弹旅(团)的中继级维修机构作用没有得到发挥，随着军队保障的社会化改革，大修厂和生产厂等基地级维修机构要充分做好装备的保障工作，任务加重，这样形成了装备基层级负责使用，基地级维修机构负责“售后服务”的二级保障体制，更有利于装备保障的社会化改革。

2 维修技术人力资源系统系统动力学模型

系统动力学模型(System Dynamics,SD)被誉为实际系统的实验室，是由美国麻省理工学院(MIT)J.W.Forrester教授在1960年提出的运用功能、历史、结构相结合的一种方法，借助于计算机仿真而定量地研究非线性、多重反馈、复杂时变的系统分析技术[5-6]。SD加强了与最优化技术应用、参数估计、灵敏度分析、结构稳定性分析、系统科学、控制理论等方面的联系，在世界范围内得到了广泛地应用和传播，取了许多新发展[7-8]。该方法在能力评估、安全管理和库存管理等众多领域广泛应用[9-12]。对于维修体制来说，二级、三级体制各有利弊，但对于目前的研究现状来看，对于二级和三级体制的优缺点没有定量化的说明，很难确定适合采用二级或三级维修体制的条件。本文就这一问题进行初步研究，主要分析两种体制的优缺点，将维修保障技术人力系统中的支援抢修维修技术人力资源系统部分，运用系统动力学理论，分别进行讨论分析，在新装备研制阶段，如何选择其维修体制提供一定的决策依据。

目前，地空导弹武器装备支援抢修系统流程为：发生故障的武器装备进入部队一级维修，完成维修后立即投入使用，一级维修不了的装备转入二级维修[13]。若采用二级体制，如部队出现基层级无法排除的故障，则直接申请基地级支援抢修，这样两种体制下系统的平均支援抢修时间也不相同，在支援抢修时间满足战备要求的情况下，该如何选择维修体制是需要解决的问题。

2.1 支援抢修系统因果关系

支援抢修系统的因果关系如图1所示，重点分析不同体制下维修人员与平均维修时间的关系。

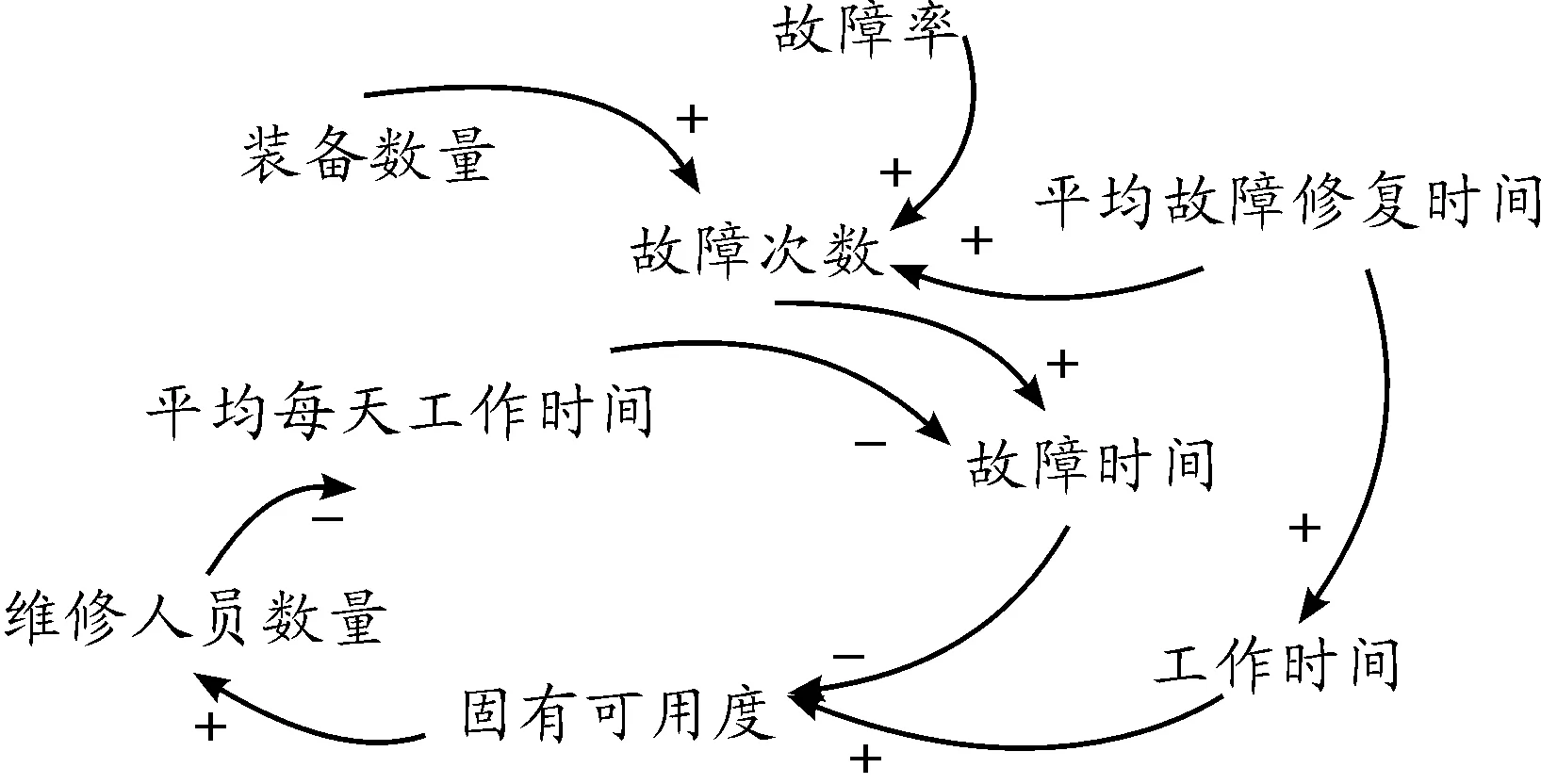
图1 支援抢修系统因果关系

2.2 支援抢修系统流图

将以上的因果关系进行变量分门别类，构建备件系统流图。如图2所示，模型中共有33个变量，其中流位变量有5个，流率变量有5个，其他变量有23个，各变量的符号表示与定义如表1所示。

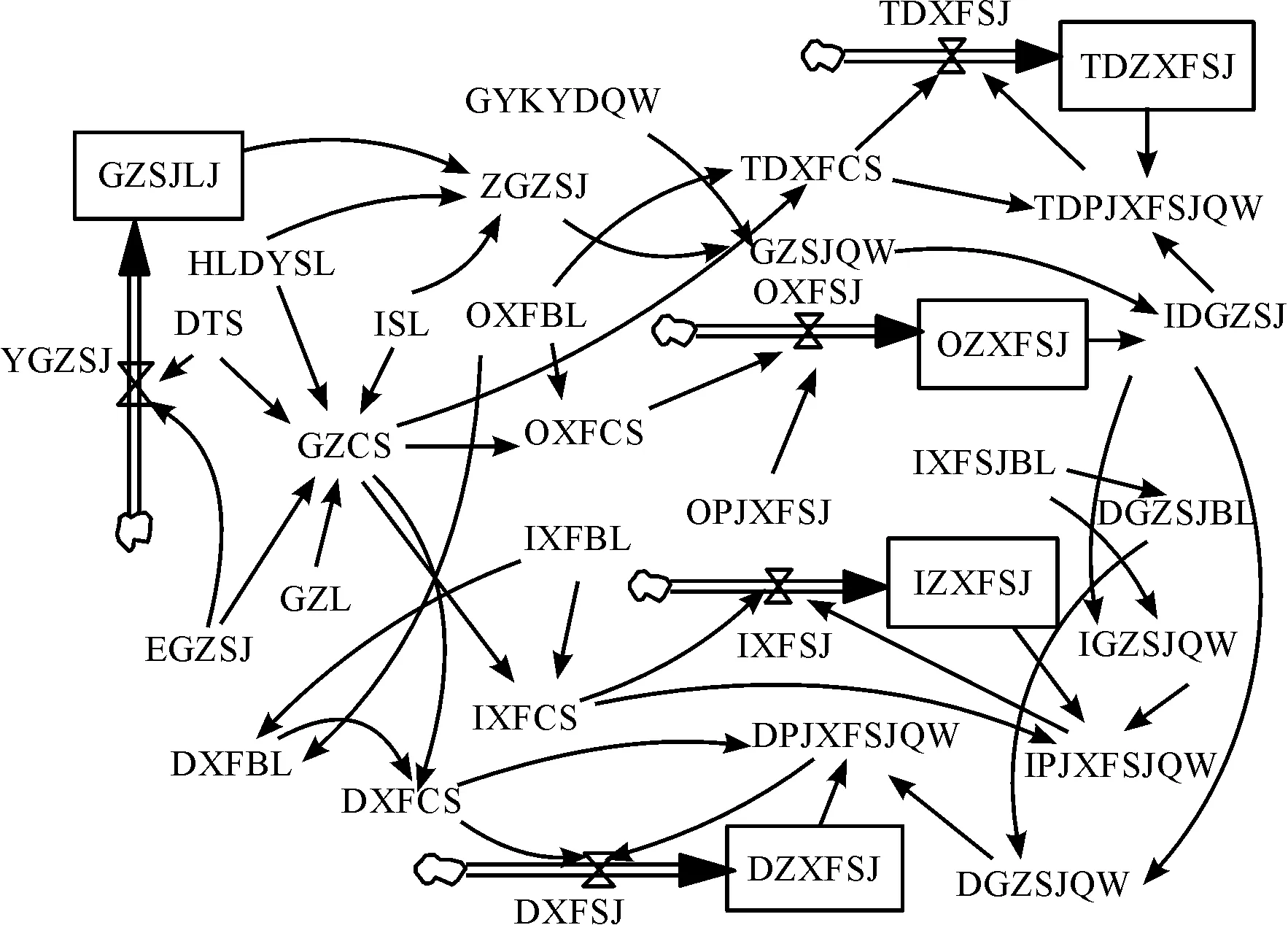
图2 支援抢修系统流图

3 支援抢修系统SD模型仿真分析

根据系统流图(图2)运用系统动力学仿真软件(Vensim PLE 32),通过对仿真结果的分析，可以得到两种体制下支援抢修系统平均修复时间的指标要求，这样可更好的判断采用二级体制的时机。

表1 变量的符号表示与定义

3.1 仿真假设

1)整个系统共30个火力单元，三级体制下分为：6中继级维修机构，1个基地级维修机构；二级体制则分为：30个火力单元和1个基地级维修机构。

2)在同一级的维修机构的不同维修人员修复能力水平一样，也就是对于故障的平均修理时间是相同的；但维修人员数量只对故障的等待修理时间有影响，对故障的处理时间没影响。

3)假定目前的部队三级维修体制实际情况下，基层级约能修复全部故障的60%，中继级35%，基地级5%，装备平均每天工作2 h；基层级的平均故障修复时间不超过0.5 h。

4)两种体制都采用固有可用度来度量，固有可用度指标仅与修复性维修时间和工作时间有关的一种可用性参数[14]，本系统假设两种体制下的维修保障系统固有可用度指标都为AI=0.9的条件下进行比较分析，其固有可用度计算公式为[15]

(1)

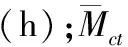
3.2 仿真分析

1)系统平均无故障时间(MTBF)对两种体制下支援抢修系统的影响。在MTBF从30 h增加到60 h和支援抢修系统的修复比例不变的情况下，基层级的平均故障修复时间不变，随着MTBF的增加，三级体制下，各级支援抢修系统平均修复时间的变化，如图3所示。

图3 三级体制下平均修复时间与MTBF的变化图

对于中继级支援抢修系统的平均修复时间的指标来说，在保持固有可用度一定的情况下，装备MTBF增加，单位周期内故障次数减少，在总的工作时间一定时，总的故障时间一定，所以平均修复时间就要增加，从图3中可以看出，MTBF从30 h增加到60 h，中继级平均修复时间要从7 h增加到12 h左右；基地级平均修复时间要从18 h增加到38 h左右，这对支援抢修系统的要求降低。

若采用二级维修体制，在基层级的修复能力约为60%的情况下，二级体制下的基地级平均修复时间与MTBF变化的关系如图4所示。随着MTBF从30 h增加到60 h，二级体制下基地级平均修复时间从8 h增加到16 h左右，这样的指标要求对于基地级维修来说是很难满足的。根据目前基地级的抢修能力，一般来说，基地级距基层级约有1 000多km，其平均修复时间都要在4 d(32 h)左右，所以这种情况下，如果采用二级维修体制，一要增加装备的平均无故障时间MTBF，提高装备的可靠性；二是增加基层级的修复能力，这样基地级的修复次数减少，在同样允许的修复时间条件下，基地级平均修复时间就会增加，符合基地级的要求；三是对基地级的修复手段进行改进，目前来说，基地级支援抢修，花在路途上的时间约有1/3，如果采用远程支援技术，可将路途时间全部节省，将会大大降低基地级的平均故障修复时间，使其满足二级体制的要求。

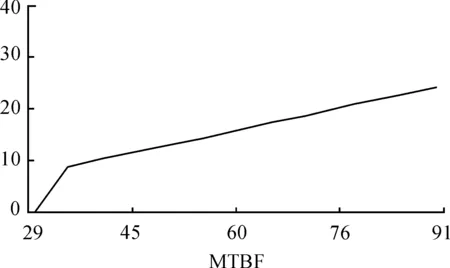
图4 二级体制下平均修复时间与MTBF变化图

2)平均每天工作时间(EGZSJ)的影响。在装备平均无故障时间MTBF为50 h的情况下，平均每天工作时间从2 h到6 h的变化下，若采用三级体制，各级的平均修复时间指标变化如图5所示；二级体制的平均修复时间指标变化如图6所示。

图5 三级体制下平均修复时间与EGZSJ的变化图

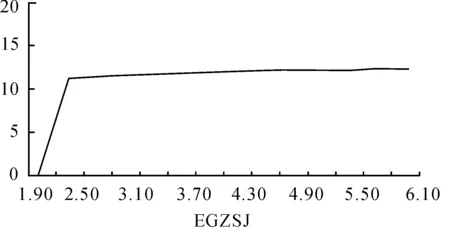
图6 二级体制下平均修复时间与EGZSJ的变化图

从图5和图6可以看出：随着平均每天工作时间EGZSJ的增加，两种体制下，各级的平均修复时间都有所增加，幅度都不大，这种上升的趋势可用固有可用度的定义来解释。将固有可用度定义公式进行变换可得：

(2)

从式(2)可以看出：在三级体制下，随着EGZSJ的增加，中继级和基地级的平均修复时间指标都略有增加，较符合目前装备维修保障的实际；但在二级体制下，随着EGZSJ的增加，基地级平均修复时间指标略有增加，当EGZSJ为6 h时，二级体制的基地级平均修复时间指标最大值为13 h，就目前各基地级维修机构都不能满足此要求。

3)修复比例的影响。新型装备中继级修复能力在减弱，基层级和基地级修复能力太强，所以就提出要向两级体制转变的趋势，这里就以修复比例来体现各级的修复能力，修复比例的计算公式为

(3)

式(3)中：O、I和D分别表示基层级、中继级和基地级；CO表示基层级修复的故障次数，I和D类推；PO表示基层级修复比例，I和D类推。

随着基层级修复比例OXFBL的增加，两种体制的平均修复时间指标变化如图7和图8所示，在OXFBL为0.8时，三级体制下，中继级平均修复时间指标要求达到16 h左右，基地级平均修复时间指标要求达到28 h左右，如图7所示；而在二级体制下，基地级平均修复时间指标要求达到30 h左右，这对于目前装备支援抢修系统来说是可以满足其要求的，也就是在OXFBL大于等于0.8时，可以采用二级体制。

图7 三级体制下平均修复时间指标与OXFBL的变化关系图

图8 二级体制下平均修复时间指标与OXFBL的变化关系图

4)远程支援技术的影响。故障处理时间如图9所示。三级体制下，不同级别的维修机构对于装备故障处理时间都有一个平均值，比如说路途时间，中继级到基层级的平均距离约200 km，平均花费3 h，而基地级距基层级至少1 000 km，一般要花一整天时间，这里就以一个工作日(8 h)为单程路途平均时间，这样可得中继级和基地级各项数据如表2所示。

图9 故障处理时间关系图

表2 两级时间

注：括号内为二级体制下时间

从表2可以看三级体制下，中继级最小故障平均修复时间8.5 h，基地级为33 h。如果对传统的维修技术手段不进行改进的话，结合前面的分析，只有OXFBL大于等于0.8时，采用二级体制的基地级平均修复时间才能满足要求。分析上表2，花在路途的时间约50%，如果把路途时间节省下来，则采用二级体制更容易实现，可以采用远程支援技术，远程支援技术是武器装备维护保障领域发展十分迅速的一项技术，是随着高技术武器装备的大量使用和计算机网络通信技术的不断发展而产生的一种先进的装备保障手段[16]。它使一线技术人员与后方技术专家用网络紧密的联系在一起，为武器装备的管理提供及时、准确的指导。当一线技术人员遇到短时间内难以解决的故障时，可以通过互联网将装备的各种技术参数，传输给后方的技术专家，以求支援；后方的技术专家在进行分析研究后，迅速做出结论，并通过网络对前方的维护保障工作进行实时指导，协助前方人员迅速、准确地完成任务[17]。探讨应用这种技术，可以加快受损装备的维修时间，以提高武器装备的利用率，远程维修示意图如图10所示。

图10 远程维修示意图

这里针对远程支援技术，提出一种远程支援技术因子，用百分比PYZJ表示，它含义为有一定百分比PYZJ的维修任务可以通过远程支援技术来实施，这样，二级体制下，基地级的平均故障处理时间与远程支援技术因子的关系如图11所示，其最小处理时间是在PYZJ=1时，TDPJXFSJmin=16.5 h。

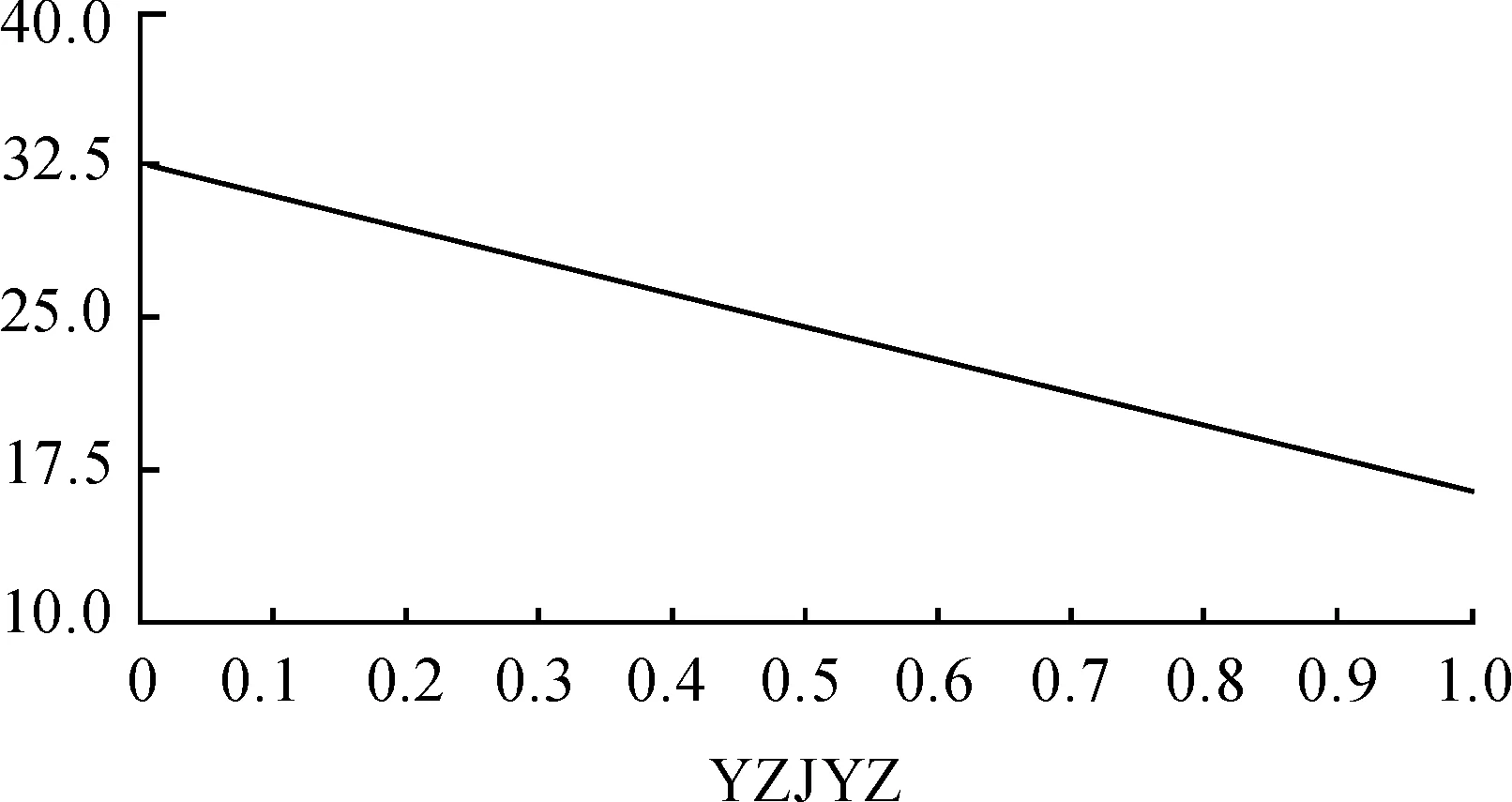
图11 二级体制下基地级平均故障处理时间与PYZJ的关系图

3.3 参数分析

在以上的系统中，努力提高一些参数，如基层级修复比例等，可以大大降低维修保障系统的指标要求，因此，模型具有一定的实用性。通过对MTBF、EGZSJ、修复比例和远程支援技术的分析，综合考虑可得在采用二级体制下的装备MTBF、EGZSJ、基层级修复比例OXFBL和远程支援技术之间的关系。

1)MTBF与PYZJ的关系。在图5中，OXFBL=0.6，EGZSJ=2，只有在MTBF≥60时，才能满足该要求TDPJXFSJ≥TDPJXFSJmin，实行二级体制。因此分析在60≤MTBF≤120间PYZJ的关系图，如图12，从图中可看出不同的MTBF对PYZJ的最低要求值，MTBF越大，对远程支援技术要求就越低。