关于半对偶模的若干特殊模类*

何东林 李煜彦

(陇南师范高等专科学校数信学院，甘肃 陇南 742500)

0 引 言

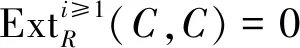
设C是半对偶模.由满足下列条件的模M组成的类为Auslander类,记为AC：

且典范同态μCCM：M→HomR(C,C⊗M)为同构.

对偶地,由满足下列条件的模N组成的类为Bass类,记为BC(详见[2])：

且典范同态υCCN：C⊗HomR(C,N)→N为同构.

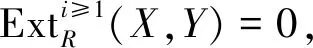
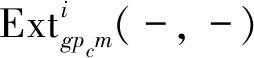
表示模M的示性模.受此启发,本文主要讨论具有有限C-投射分解和C-Gorenstein投射分解的模类的一些正交性质.文中C均指固定的半对偶模,其余概念和记号参见文献[5-8].

1 主要结论

引理1[4]gpc⊥pc.

命题1以下关系成立:

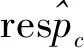
(3)由(1)和(2)易证.

为了便于讨论,下面均设R为具有对偶模D的Cohen-Macaulay环,C+=HomR(C,D).由文献[3]易知C+也是半对偶模.

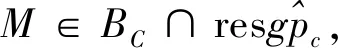
证明由M∈BC及[4]知,M具有真pc分解

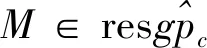
Χ+≡0→Xn→Xn-1→…→X1→X0→M→0,

其中Xi∈pc.可见复形Χ有界.由引理1知gpc⊥pc,所以用HomR(gpc,-)作用于Χ+仍正合.从而Χ是真gpc-分解.因此Χ既是有界真pc-分解又是有界真gpc-分解.

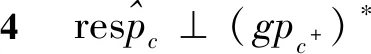
推论1设(ε1)：0→Pn→Pn-1→…→P2→P1→P0→K→0是R模正合列,其中Pi∈pc(i=0,1,…n).则对任意M∈gpc+,(ε)在函子HomR(-,M*)下仍正合.

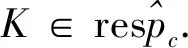
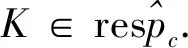
0→HomR(H,M*)→HomR(G,M*)→HomR(K,M*)→0,

(1)

正合.又由推论1知序列(1)在HomR(-,M*)下仍正合.即序列

0→HomR(K,M*)→HomR(P0,M*)→HomR(P1,M*)→…→HomR(Pn,M*)→0,

(2)

正合.由正合列(1)和(2)拼接可得长正合列

0→HomR(H,M*)→HomR(G,M*)→HomR(P0,M*)→…→HomR(Pn,M*)→0,

因此(ε)在HomR(-,M*)下仍正合.

引理2[1]gpc关于任意直和、直和因子及满同态的核封闭.

命题5设0→A→G1→G0→M→0为R-正合列,其中G0,G1∈gpc.则存在正合列0→A→P⊗C→G→M→0和0→A→H→Q→M→0,其中P,Q为投射模且G,H∈gpc.

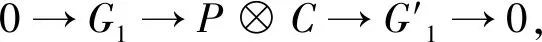
推出图1

推出图2

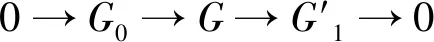
根据引理2知G∈gpc.将正合列0→A→P⊗C→B→0与0→B→G→M→0拼接易得正合列

0→A→P⊗C→G→M→0,

(3)

其中P为投射模且G∈gpc.

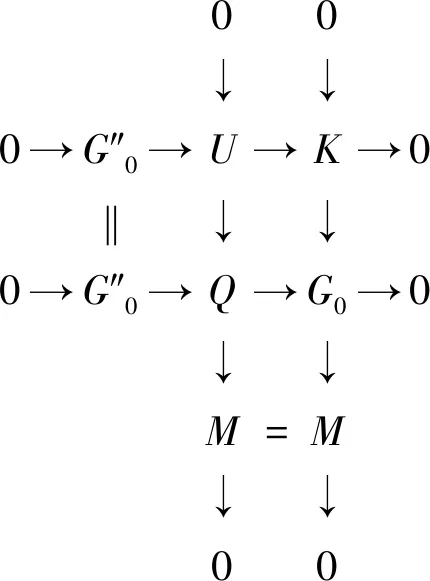
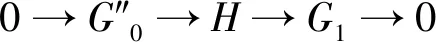
由引理2知H∈gpc.将短正合列0→A→H→U→0和0→U→Q→M→0拼接易得正合列

0→A→H→Q→M→0,

(4)

其中Q为投射模且H∈gpc.

定理1设0→K→Gn-1→…→G1→G0→M→0为R-正合列,其中Gi∈gpc(i=0,1,…,n-1).则以下结论成立：

(i)存在正合列0→K→Pn-1⊗C→…→P1⊗C→P0⊗C→U→0和0→M→U→G→0,其中Pi(i=0,1,…,n-1)为投射模且G∈gpc;

(ii)存在正合列0→V→Qn-1→…→Q1→Q0→M→0和0→V→H→K→0,其中Qi(i=0,1,…,n-1)为投射模且H∈gpc.

证明对n用数学归纳法.

(i)当n=1时,0→K→G0→M→0正合,其中G0∈gpc.由gc投射模的定义知,存在短正合列0→G0→P0⊗C→N→0,其中P0为投射模且N∈gpc.考虑如下推出图5.

推出图5

易知0→K→P0⊗C→U→0和0→M→U→N→0就是满足要求的正合列.

假设结论对于任意整数k(2≤k

0→K→Pn-1⊗C→…→P1⊗C→U′→0,

(5)

0→L→U′→G′→0,

(6)

其中Pi(i=1,…,n-1)为投射模且G′∈gpc.考虑如下推出图6.

推出图6

由G0,G′∈gpc及引理2知X∈gpc.可见存在正合列0→X→P0⊗C→G→0,其中G∈gpc且P0为投射模.构造如下推出图7.

推出图7

将正合列0→U′→P0⊗C→U→0与(5)拼接可得正合列

0→K→Pn-1⊗C→…→P1⊗C→P0⊗C→U→0,

(7)

显然正合列(7)与推出图(7)的第3列0→M→U→G→0就是满足要求的正合列.从而结论对于n-1也成立. (ii)证明过程与(i)类似.