浅议初中数学课堂中学生讲题能力的培养
2020-04-20李惠玲
李惠玲

【摘要】 在数学课堂中实施“学生讲题”活动,更好地体现以学生的学习为核心,凸显学生的主体性,让学生的学习从被动转变到主动,进一步提高数学能力,让数学课堂活起来。
【关键词】 初中数学 学生讲题 能力培养
【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2020)09-051-01
一、提出启发性的问题,引领学生讲题
学生走上讲台在讲题过程中,对学生来说是个全新的挑战,学生往往会出现语言表达不准确、说理过程不精准、解题过程不完整等等不足之处,此时教师尤为重要,教师可在关键处或错误处提出有启发性的问题可以引导台上的学生思考,也引起台下学生的共鸣,同时引起全部学生对知识点重视和再学习,进一步有助于学生在发生错误时迷途知返,能让学生在理解重点处画龙点睛,能让学生偏离主题时“拨乱归正”,能让学生在理解肤浅时趋于深入、接触本质。
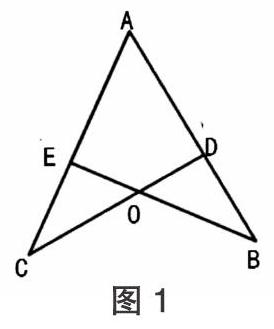
案例4:如图1,CD和BE相交于点O,AB=AC,添加一个条件使得△ABE≌△ACD.
讲题学生:我发现要证△ABE≌△ACD,已有一组公共角∠A=∠A,还有AB=AC,根据全等三角形的判定方法“SAS”可添CD=BE.
教师:赞同的请举手。
教师巡视一遍发现还是有几个学生赞同的。
教师:判定方法“SAS”中三个条件对应相等满足怎样位置关系?
听课学生:两边和它们的夹角分别对应相等。
教师:那这个同学找CD=BE满足这个条件吗?
讲题学生:我知道了,我知道了,添AD=AE就可以了。(讲题学生幡然醒悟)
教师:非常好,还可以添加什么条件呢?(眼神转向听课学生)
听课学生开始七嘴八舌讨论,讲题学生拿着粉笔在黑板上笔划。
讲题学生:我知道了!(听课学生顿时安静下来,盯着讲题学生)还可以添∠B=∠C,这样就满足“ASA”这个判定方法;还可以添∠ADC=∠AEB,这样就满足“AAS”这个判定方法了。
教师:分析得非常有道理,你很棒!
在学生讲题的过程中,教师适时的有效追问和点评可以指引学生朝着正确的方向发展,以免跑偏。教师及时对学生的肯定,讓学生感受到老师对他讲题的某一细节的认可、欣赏,更能给学生带来长久的激励和导向作用。
二、放手让学生讲题,是学生创造力的再生
学生讲题可以激发学生的创造力,教师在平时教学中要大胆放手让学生去讲题,往往学生会给你带来意想不到的结果,学生讲题不仅对讲题学生来说一个挑战,对教师来说也是一个挑战。学生通过讲题,解题思维得到了再次的验证,同时在讲题过程中学生的创造力也给激发出来,会根据自己认知去改变讲题的模式,听课学生反而给讲题学生带进了解题的世界。
案例6:题目:已知如图2,△DAC,△EBC均是等边三角形,点A,C,B在同一条直线上,且AE,BD分别与CD,CE交于点M,N.
求证:(1)AE=DB;
(2)△BCN≌△ECM;
(3)△CMN为等边三角形.
讲题学生:根据已知条件要证AE=DB,就要证△ACE≌△DCB全等,因为△DAC,△EBC是等边三角形,得到AC=DC、EC=BC,再根据计算得到∠ACE=∠DCB,再根据判定方法“SAS”得到两个三角形全等,从而得到AE=DB.
教师:你根据什么得到∠ACE=∠DCB?
讲题学生(圈图表示):有两种方法可以得到?
教师:哦!还有两种方法?你说说!
讲题学生:第一种方法根据等边三角形的性质得到∠ACD=∠ECB=60°,由于点A、C、B在同一条直线上,则有∠ACD+∠DCE=∠ECB+∠DCEJ即∠ACE=∠DCB;第二种方法同样根据等边三角形的性质得到∠ACD=∠ECB=60°,根据邻补角的性质得到180°-∠ACD=180°-∠ECB,从而得到∠ACE=∠DCB.
听课学生:鼓掌,眼中露出钦佩的眼神。
教师:讲得很好!我们继续前进。
讲题学生:要证△BCN≌△ECM,同样根据等边三角形的性质得到BC=EC,∠NCB=∠MCE=60°,还差一个条件,你们找一找!
教师:还考起同学来了!同学们找找,还差一个条件,根据全等三角形的判定方法差的这个条件是边呢?还是角?
听课学生:叽叽喳喳地讨论起来。
听课学生甲:不能找边,因为现在已有的条件是一边一角,若要再找一组边对应相等,只能按两边夹一角的条件去找,但是没有CM=CN.
听课学生乙:再找一组角对应相等,可以根据全等三角形的判定方法中的“ASA”和“AAS”去寻找。
教师邀请讲题学生给同学们答疑。
讲题学生:由(1)知△ACE≌△DCB可得∠AEC=∠DBC,刚好是△BCN和△ECM的一组对应角,从而根据判定方法“ASA”可证得△BCN≌△ECM.
听课学生:送上热烈的掌声。
讲题学生:进入第三问啦!要证明△CMN是等边三角形,有三个思考的方向:一是证△CMN的三条边相等;二是证△CMN的三个内角都相等;三是一个角是60°+等腰三角形,而等腰三角形只要得到任意两条边相等即可。选哪个呢?其实答案已经在第二问就解决了,谁知道?
教师:卖关子了!谁知道?
听课学生丙:第二问已证△BCN≌△ECM,可以得到CM=CN,说明△CMN是等腰三角形,而第二问中已说明∠DCE=60°,所以根据一个角是60°+等腰三角形从而说明△CMN为等边三角形。
讲题学生:同学们,丙同学说理有没有问题?
听课学生:没问题!
教师:还偷起懒来了,叫你讲题,你倒好,叫起其他同学来了。不过讲得真好!
全班学生爆出了热烈的掌声。
在讲题交流中,不仅较好地突破了学生的认知障碍,而且丰富了学生的解题经验,教师的适时点拨和讲评,让不同的认知及时转化,促使学生的认知水平不断上升,从而让学生看到不变的数学本质。
在初中数学课堂中搭建平台让学生讲题,提高了学生学习数学的兴趣,让学生积极主动地参与到课堂教学活动,提高了学生的数学能力和数学语言的表达能力,实现了自身的价值,享受到学习数学的快乐,不仅会学数学,还会将数学。
[ 参 考 文 献 ]
[1]刘东升.让学生在“讲题”中提高数学能力[J].数学中学教学参考,2011年7月.
[2]欧阳秋霞.基于“四整合教学”下初中数学“学生讲题”的教学举措探究[J].中学数学研究,2017年第11期.
